上篇博文-数据结构-绪论(一)
👉数据结构-绪论(一)
本文包括了数据结构的算法基本概念,着重讲了时间复杂度和空间复杂度。
有具体的例子。Let’s go!🏃♂️
数据结构
绪论(二)
思维导图

1.3 算法
程序
=
数据结构
+
算法
定义:
算法 (Algorithm) 是为了解决某类问题而规定的一个有限长的操作序列。
(求解问题的步骤)
1.3.1 算法的特性
一个算法必须满足以下五个
重要特性
。
有穷性
。一个算法必须总是在执行有穷步后结束,且每一步都必须在有穷时间内完成。
确定性
。对千每种情况下所应执行的操作,在算法中都有确切的规定,不会产生二义性, 使算法的执行者或阅读者都能明确其含义及如何执行。
可行性
。算法中的所有操作都可以通过已经实现的基本操作运算执行有限次来实现。
输入
。一个算法有零个或多个输入。当用函数描述算法时,输入往往是通过形参表示的, 在它们被调用时,从主调函数获得输入值。
输出
。一个算法有一个或多个输出,它们是算法进行信息加工后得到的结果,无输出的 算法没有任何意义。当用函数描述算法时,输出多用返回值或引用类型的形参表示好算法的特质
正确性
。算法应能够正确地解决求解问题。
可读性
。算法应具有良好的可读性,以帮助人们理解。
健壮性
。输入非法数据时,算法能适当地做出反应或进行处理,而不会产生莫名其妙的输出结果。
高效率与低存储量需求
。花的时间少。时间复杂度低,不费内存。空间复杂度低
1.3.2 时间复杂度
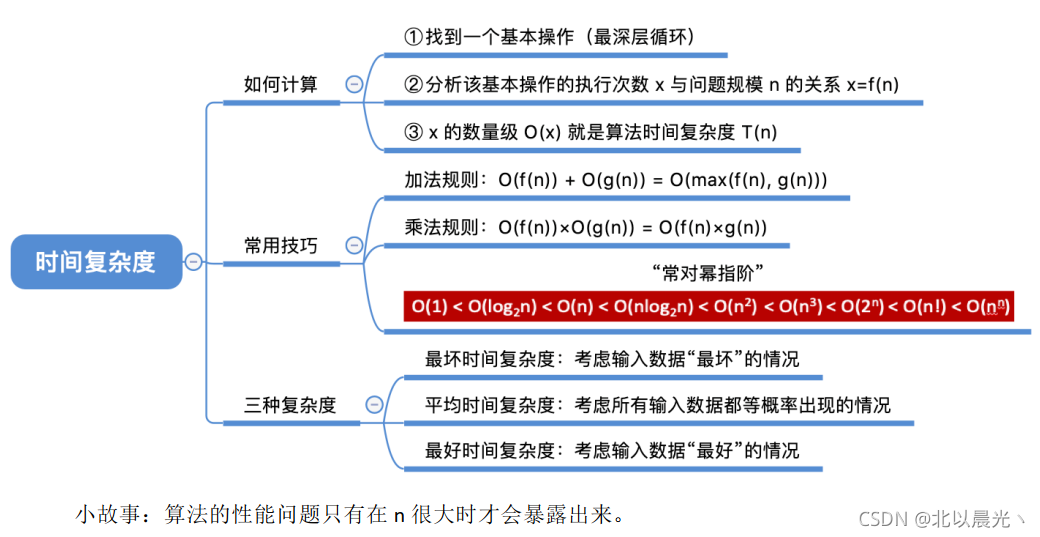
定义:
事前预估算法时间开销T(n)与问题规模 n 的关系
(T 表示 “time”)(1)
加法规则
:多项相加,只保留最高阶的项,且系数变为1
T(
n
)
=
T
1
(
n
)
+
T
2
(
n
)
=
O
(
f
(
n
)
)
+
O
(
g
(
n
)
)
=
O
(
m
a
x
(
f
(
n
)
,
g
(
n
)
)
)
T(n) = T_1(n) + T_2(n) = O(f(n)) + O(g(n)) = O(max(f(n), g(n)))
T
(
n
)
=
T
1
(
n
)
+
T
2
(
n
)
=
O
(
f
(
n
)
)
+
O
(
g
(
n
)
)
=
O
(
m
a
x
(
f
(
n
)
,
g
(
n
)
)
)
(2)
乘法规则
:多项相乘,都保留
T(
n
)
=
T
1
(
n
)
×
T
2
(
n
)
=
O
(
f
(
n
)
)
×
O
(
g
(
n
)
)
=
O
(
f
(
n
)
×
g
(
n
)
)
T(n) = T_1(n)×T_2(n) = O(f(n))×O(g(n)) = O(f(n)×g(n))
T
(
n
)
=
T
1
(
n
)
×
T
2
(
n
)
=
O
(
f
(
n
)
)
×
O
(
g
(
n
)
)
=
O
(
f
(
n
)
×
g
(
n
)
)
O(
1
)
<
O
(
l
o
g
2
n
)
<
O
(
n
)
<
O
(
n
l
o
g
2
n
)
<
O
(
n
2
)
<
O
(
n
3
)
<
O
(
2
n
)
<
O
(
n
!
)
<
O
(
n
n
)
O(1) < O(log_2n) < O(n) < O(nlog_2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
O
(
1
)
<
O
(
l
o
g
2
n
)
<
O
(
n
)
<
O
(
n
l
o
g
2
n
)
<
O
(
n
2
)
<
O
(
n
3
)
<
O
(
2
n
)
<
O
(
n
!
)
<
O
(
n
n
)
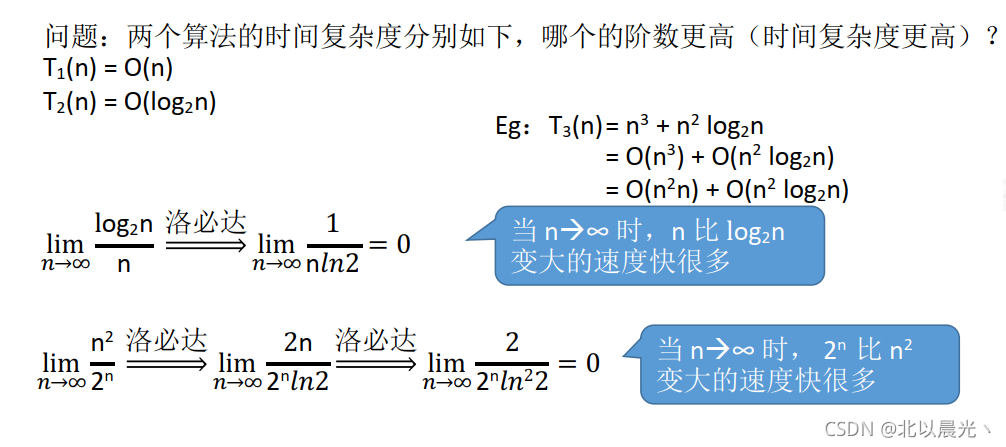
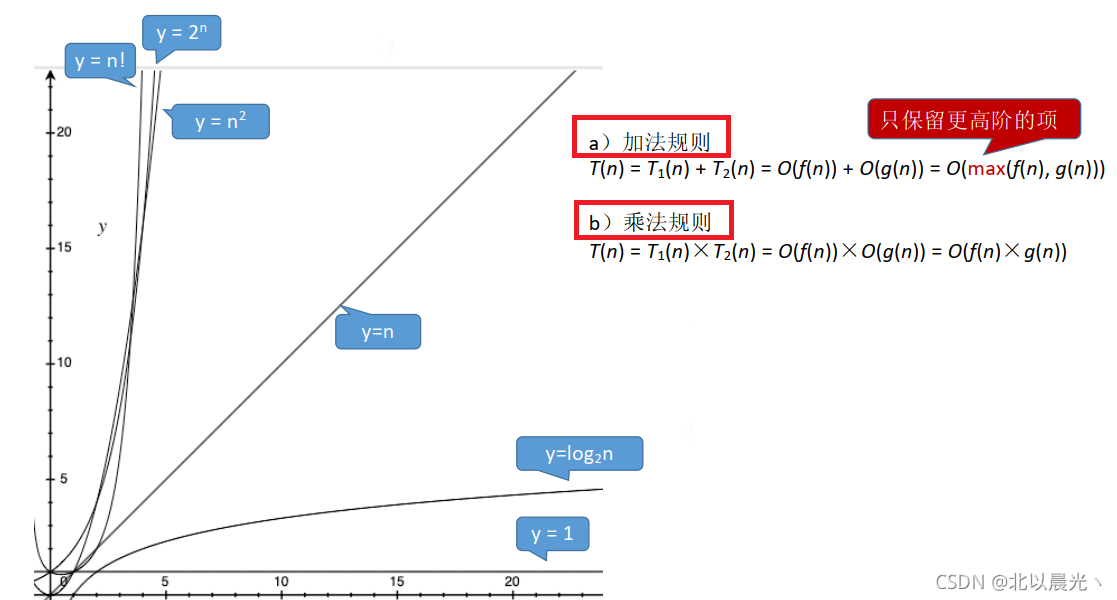
例子
🌰
1、逐步递增型
int main(){
loveYou(3000);
}
void loveYou(int n) { //n为问题规模
① int i = 1;
② while(i <= n) {
③ i++;
④ printf("I love you %d\n", i);
}
⑤ printf("I love you more than %d\n", n);
}
语句频度:
① 1次
② 3001次
③④ 3000次
⑤ 1次
T(3000) = 1 + 3001 + 2*3000 + 1
时间开销与问题规模 n 的关系:
T(n) = 3n+3 =
O(n)
2、嵌套循环性
void loveYou(int n) { //n为问题规模
int i = 1;
while(i <= n) { //外层循环执行n次
i++;
printf("I love you %d\n", i);
for(int j = 1; j <= n; j++) { //嵌套两层循环
printf("I am Iron Man\n"); //内层循环共执行n^2次
}
}
printf("I love you more than %d\n", n);
}
时间开销与问题规模 n 的关系:
T(
n
)
=
O
(
n
)
+
O
(
n
2
)
T(n) = O(n) + O(n^2)
T
(
n
)
=
O
(
n
)
+
O
(
n
2
)
=
O(
n
2
)
O(n^2)
O
(
n
2
)
3、指数递增型
void loveYou(int n) { //n为问题规模
int i = 1;
while(i <= n) { //一次循环
i = i * 2; //每次翻倍
printf("I love you %d\n", i);
}
printf("I love you more than %d\n", n);
}
计算上述算法的时间复杂度 T(n):
设最深层循环的语句频度(总共循环的次数)为 x,(
i=
2
x
i = 2^x
i
=
2
x
)则由循环条件可知,循环结束时刚好满足
2x
>
n
2^x > n
2
x
>
n
x=
l
o
g
2
n
+
1
x = log_2n + 1
x
=
l
o
g
2
n
+
1
T(n) = O(x) =
O(
l
o
g
2
n
)
O(log_2n)
O
(
l
o
g
2
n
)
4、搜索型
int main() {
int flag[n] = {1...n}; //flag数组中乱序存放了1~n这些数
loveYou(flag, n);
}
void loveYou(int flag[], int n) { //n为问题规模
printf("I am Iron Man\n");
for(int i = 0; i < n; i++) { //从第一个函数中查找
if(flag[i] == n) { //找到
printf("I love you %d\n", n);
break;
}
}
}

结论
最坏时间复杂度
:最坏情况下算法的时间复杂度
平均时间复杂度
:所有输入示例等概率出现的情况下,算法的期望运行时间
最好时间复杂度
:最好情况下算法的时间复杂度
1.3.3 空间复杂度
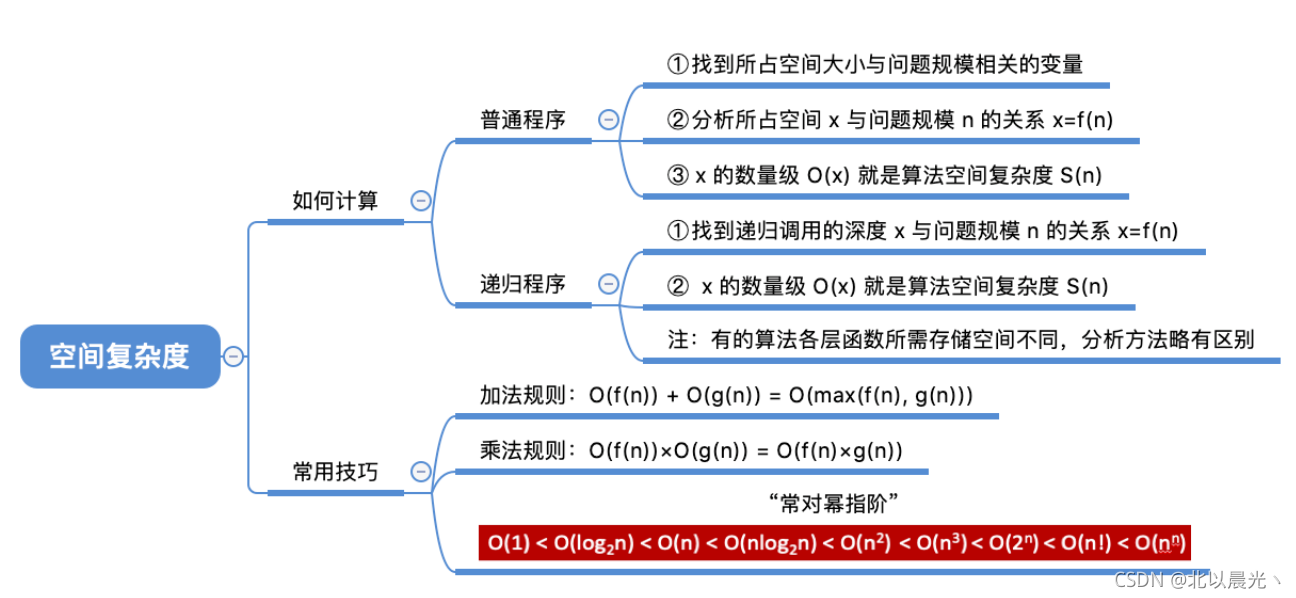
定义:
算法所需存储空间的度量,记作: S(n)=O(f(n)) 其中n为问题的规模(或大小),空间开销(内存开销)与问题规模 n 之间的关系
(1)逐步递增

(2)声明一个一维数组
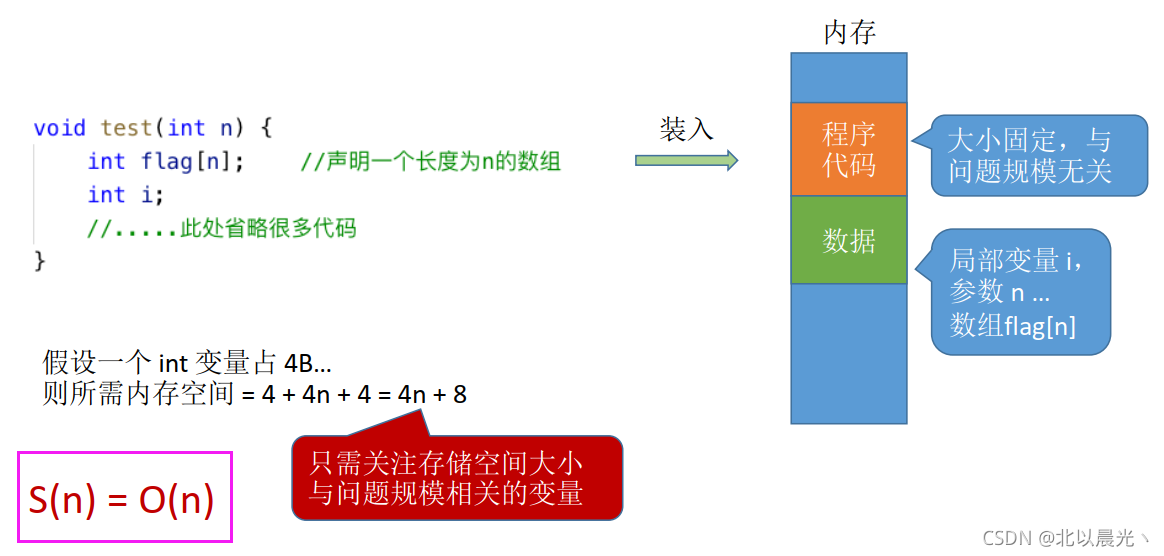
(3)声明一个二维数组

(4)声明一个二维数组,一个一维数组
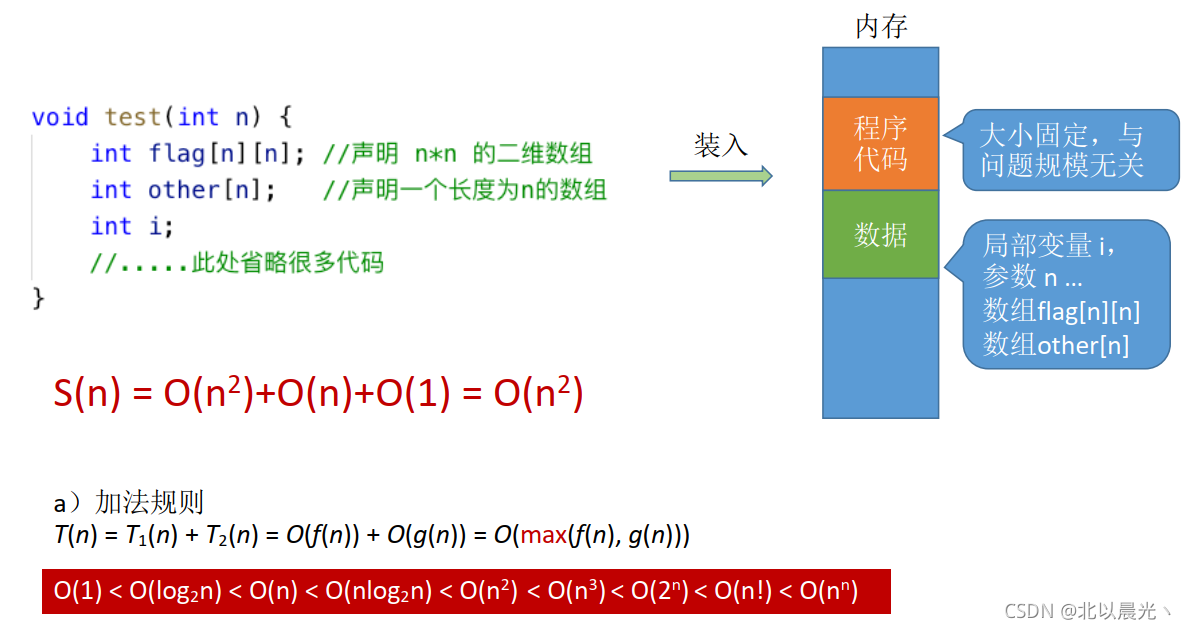
例子
1、递归型
int main() {
loveYou(5);
}
void loveYou(int n) { //n为问题规模
int a, b, c; //声明局部变量
//......
if(n > 1) {
loveYou(n - 1);
}
printf("I love you %d\n", i);
}

2、递归型
int main() {
loveYou(5);
}
void loveYou(int n) { //n为问题规模
int flag[n]; //声明一个数组
//......
if(n > 1) {
loveYou(n - 1);
}
printf("I love you %d\n", i);
}

友情连接-数据结构-线性表(一)概念及基本操作
👉数据结构-线性表(一)概念及基本操作