博客

行列式（Determinant），记作det(A)或|A|，是一个在方阵(n*n)上计算得到的标量。行列式可以看做是

有向面积或体积

的概念在一般的欧几里得空间中的推广。

书写法

矩阵A的行列式记作det(A)，行列式经常使用竖直线记法

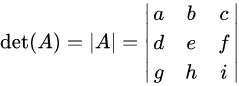
行列式在二维欧氏空间的几何意义

在一个二维平面上，两个向量和的行列式是X=(a,c)和X′=(b,d)的行列式是：





当系数是实数时，行列式表示的是向量X和X’形成的平行四边形的

有向面积

，并有如下性质：

• 行列式为零当且仅当两个
  
  向量共线
  
  （
  
  线性相关
  
  ），这时平行四边形退化成一条直线
• 以逆时针方向为正向的话，将X逆时针“转到”X’处时，扫过的地方在平行四边形里为正，否则的话面积就是负的。
• 行列式是一个双线性映射，也就是将其中的一个向量分成两个并提取单位向量，最后的面积之和是一样的
  

行列式在三维欧氏空间的几何意义

在三维的有向空间中，三个三维向量的行列式是：





当系数是实数时，行列式表示X、X’和X’’三个向量形成的平行六面体的有向体积，性质如下：

• 
  行列式为零
  
  当且仅当三个向量
  
  共线
  
  或者
  
  共面
  
  （三者
  
  线性相关
  
  ），这时平行六面体退化为平面图形，
  
  体积为零
  
  。
• 有向体积的定义，根据右手定则来约定。比如右图中（u,v,w）所形成的平行六面体的体积是正的，而 （u,w,v）所形成的平行六面体的体积是负的。
• 同样的也可以对几何体积和累加，其几何意义是指每组
  
  三个向量中
  
  如果有
  
  两个是重合
  
  的。
  
  

参考：1、

维基