问题描述:
给定n个矩阵{A1,…,An}且相邻两个矩阵是可乘的,考察这n个矩阵的连乘积问题.
· 由于矩阵乘法满足结合律,所以计算矩阵的连乘可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。
· 若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
将矩阵连乘积A.1…A简记为A[i:j],这里i<=j。
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开,i<=k<j ,则其相应完全加括号方式为(AiAi+1…Ak)(Ak+1 Ak+2…Aj)计算量: A[i:k] 的计算量加上A[k+1:j]的计算量,再加上A[i:k]和A[k+ 1:j]相乘的计算量。
分析最优解结构
特征:计算A[i:5]的最优次序所包含的计算矩阵子链A[i:k] 和A[k+1:j]的次序也是最优的。
可用反证法证明。如果问题A[i:k]存在更小开销的加括号方式,我们可以用这个更小开销的加括 号方式代替问题A[i:j]中的子问题A[i:k]的加括号方式,这样就产生问题A[i:j]的另一种具有更小开销的加括号方式,这与问题A[i:j]具有最优解(具有最小开销)矛盾。可用类似方法证明,最优解A[i:j]中的子链A[k+1:j]一定也是问题A[k+1:j]的最优加括号方式。
m矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质问题的最优子结构性质是该问题可用动态规划算法求解的显著特征。
建立递归关系
设计算A[i:j],1<=i<=j<=n, 所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]
当i=j时,A[:j]=A 为单一-矩阵,无需计算,因此,m[i,i]=0, i-1.2…n.
当i<j时,m[i,j]=m[i,k]+m[k+1,j]+ Pi-1Pk Pj;
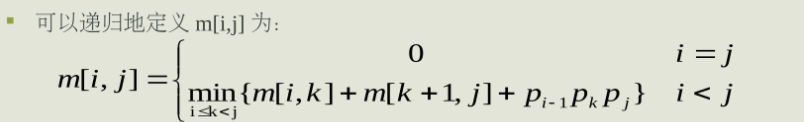
为了记录构造最优解的过程,设s[ij] 表示将AA…A.分裂产生最优解时k
的位置,即s[i,j] 等于值k,满足m[i,j]=m[i, k]+m[k+1,j]+Pi-1*Pk *Pj
计算最优值
用动态规划算法解此问题,可依据其递归式以自底向上的方式进行计算。在计算过程中,保存已解决的子问题答案。每个子问题只计算一次,而在后面需要时只要简单查- -下,从而避免大量的重复计算,最终得到多项式时间的算法。
■下面给出的动态规划算法MatrixChain中,输入参数{p0,p1,*,pn} 存储于数组p中。除了输出最优值数组m,算法还输出记录最优断开位置的数组s。
问题实例

代码实现
N = 7 # 定义矩阵的数量+1
p = [30, 35, 15, 5, 10, 20, 25]
m = [[0 for _ in range(0, N)] for _ in range(0, N)]
s = [[0 for _ in range(0, N)] for _ in range(0, N)]
def MatrixChina(n):
for r in range(2, n + 1):
for i in range(1, n - r + 2):
j = i + r - 1
m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j]
s[i][j] = i
for k in range(i + 1, j):
t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j]
if t < m[i][j]:
m[i][j] = t
s[i][j] = k
def cout(i, j):
if i == j:
print('A[', i, ']', end=' ')
return
print('(', end=' ')
cout(i, s[i][j])
cout(s[i][j] + 1, j) # 递归1到s[1][j]
print(')', end=' ')
if __name__ == '__main__':
MatrixChina(N - 1)
for i in m[1:]:
print(i[1:])
cout(1, N - 1)