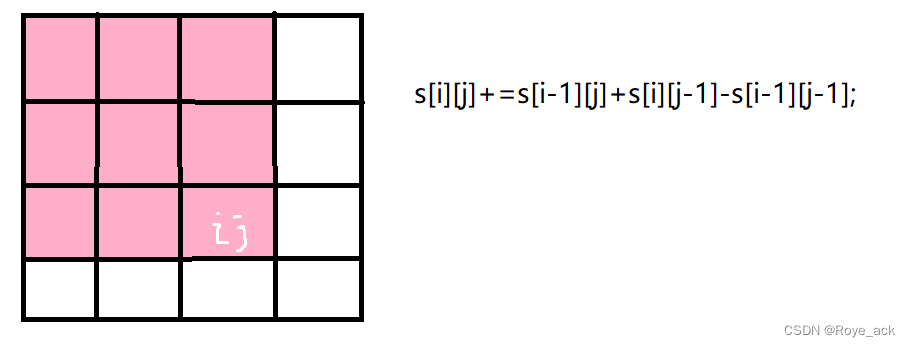目录

4402.刷题统计 – 数学模拟

4403. 修剪灌木 – 思维

4404. X 进制减法 – 进制运算 + 贪心

4405. 统计子矩阵 – 前缀和 + 双指针

1、一维前缀和

2、二维前缀和

4406. 积木画 – dp

1、找规律dp

2、状态压缩DP

4402.刷题统计 – 数学模拟

4402. 刷题统计 – AcWing题库

思路：

共n题，周一到周五5天刷a题，周六到周日2天刷b题

则一周7天刷5*a+2*b题

res+=n/(5*a+2*b)*7  //整周

剩下的题不到一周就能刷完

开辟一个数组存入一周的刷题数 day={a,a,a,a,a,b,b}

看最后还要x天能刷完

res+=x

import java.util.*;

class Main
{
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        long a=sc.nextLong(),b=sc.nextLong(),n=sc.nextLong();
        long x=a*5+b*2;
        long res=n/x*7;
        n%=x;
        long[] day={a,a,a,a,a,b,b};
        for(int i=0;n>0;i++)
        {
            n-=day[i];
            res++;
        }
        System.out.print(res);
    }
}

4403. 修剪灌木 – 思维

4403. 修剪灌木 – AcWing题库

思路：

灌木先长高再被修剪

比如第4棵，它刚刚被修剪完时高度为0

爱丽丝去修剪3时，其高度为1

去修剪2时，其高度为2

去修剪1时，其高度为3

去修剪2时，其高度为4

去修剪3时，其高度为5

因为先长高再修剪，所以在爱丽丝修剪4之前，4先长到最大高度6 

所以res就是max(i-1,n-i)*2

import java.util.*;

class Main
{
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        for(int i=1;i<=n;i++)
        {
            int x=Math.max(n-i,i-1);
            System.out.println(2*x);
        }
    }
}

4404. X 进制减法 – 进制运算 + 贪心

4404. X 进制减法 – AcWing题库

思路：

根据题目要求，X进制定义：每一位进制都不同

比如X进制数321  高位进制为8 第二位进制为10 低位进制为2

 = 3×10×2+2×2+1 = 65

解释：

• 十位的2由个位进位2次得到，所以是2×2；
• 百位的3由十位进位3次得到，十位又由个位进位得到，所以是3×10×2

由此可以得出：

• X进制中第 i 位的权重是所有 j (0 ≤ j < i)位进制的乘积
• 而转化为十进制的结果为：(每一位数×权重)之和
• 所以要让A-B最小，也就是让权重最小，也就是让每一位的进制在合法的情况下最小

题目保证A≥B，A和B的位数可能不同，需要个位数对齐，高位补零

所以我们逆向存储，低位在前，高位在后

让每一位的进制在合法的情况下最小，合法情况：进制数≥该位上的数 且 不低于2进制

因此 每一位上的最小进制数=max(a[i]+1,b[i]+1,2)

然后计算每一位的权重，其中第一位权重为1，其余位权重等于之前位的权重之积

接着计算A值和B值（位数×权重 之和），输出A-B

import java.util.*;

class Main
{
    static int N=100010;
    static int mod=1000000007;
    static long[] a=new long[N],b=new long[N],jin=new long[N],w=new long[N]; //jin存每一位数的进制 w存每一位数的权重
    
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        int ma=sc.nextInt();
        for(int i=ma;i>=1;i--) a[i]=sc.nextInt(); //若两数位数不同 逆序储存-低位在前高位在后能保证个位对齐
        int mb=sc.nextInt();
        for(int i=mb;i>=1;i--) b[i]=sc.nextInt();
        
        int m=Math.max(ma,mb);
        
        for(int i=1;i<=m;i++)
            jin[i]=Math.max(Math.max(a[i]+1,b[i]+1),2); //在合法范围内(进制数应该>该位上的数)的最小进制 最小进制不能低于2 

        w[1]=1; //第一位的权重为1
        for(int i=2;i<=m;i++) w[i]=w[i-1]*jin[i-1]%mod; //计算每一位的权重
        
        long A=0,B=0;
        for(int i=1;i<=ma;i++) A=(A+a[i]*w[i])%mod;
        for(int i=1;i<=mb;i++) B=(B+b[i]*w[i])%mod;
        
        System.out.print((A-B+mod)%mod);
    }
}

4405. 统计子矩阵 – 前缀和 + 双指针

4405. 统计子矩阵 – AcWing题库

1、一维前缀和

import java.util.*;

class Main
{
    static int N=510;
    static int[][] s=new int[N][N];
    
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt(),m=sc.nextInt(),k=sc.nextInt();
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++) 
            {
                s[i][j]=sc.nextInt();
                s[i][j]+=s[i-1][j]; //计算纵向的前缀和
            }
        
        long res=0;
        for(int i=1;i<=n;i++) //上界
            for(int j=i;j<=n;j++) //下界
                for(int l=1,r=1,sum=0;r<=m;r++) //双指针求左右两列
                {
                    sum+=s[j][r]-s[i-1][r];
                    while(sum>k)
                    {
                        sum-=s[j][l]-s[i-1][l];
                        l++;
                    }
                    res+=r-l+1;
                }
        System.out.print(res);
    }
}

2、二维前缀和

import java.util.*;

class Main
{
    static int N=510;
    static int[][] s=new int[N][N];
    
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt(),m=sc.nextInt(),k=sc.nextInt();
        for(int i=1;i<=n;i++)
            for(int j=1;j<=m;j++) 
            {
                s[i][j]=sc.nextInt();
                s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1]; 
            }
        
        long res=0;
        for(int i=1;i<=n;i++) //上界
            for(int j=i;j<=n;j++) //下界
                for(int l=1,r=1;r<=m;r++) //双指针求左右两列
                {
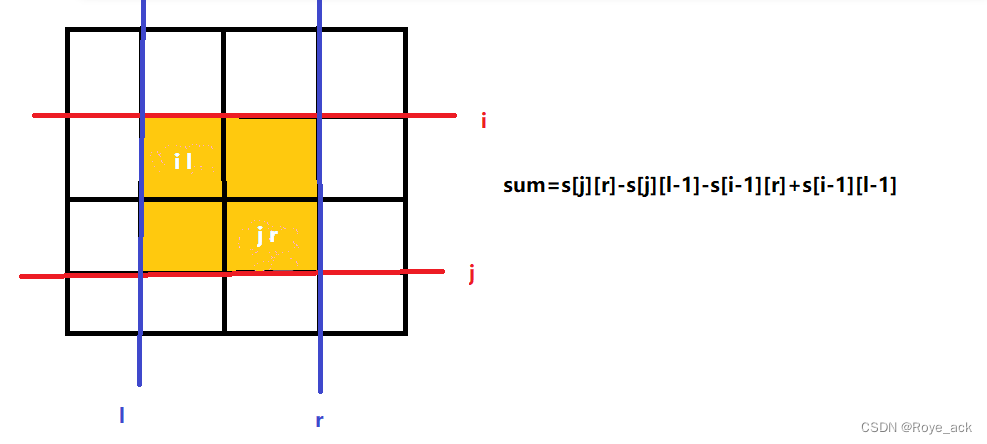
                    while(l<=r&&s[j][r]-s[j][l-1]-s[i-1][r]+s[i-1][l-1]>k) l++;
                    if(l<=r) res+=r-l+1;
                }
        System.out.print(res);
    }
}

4406. 积木画 – dp

4406. 积木画 – AcWing题库

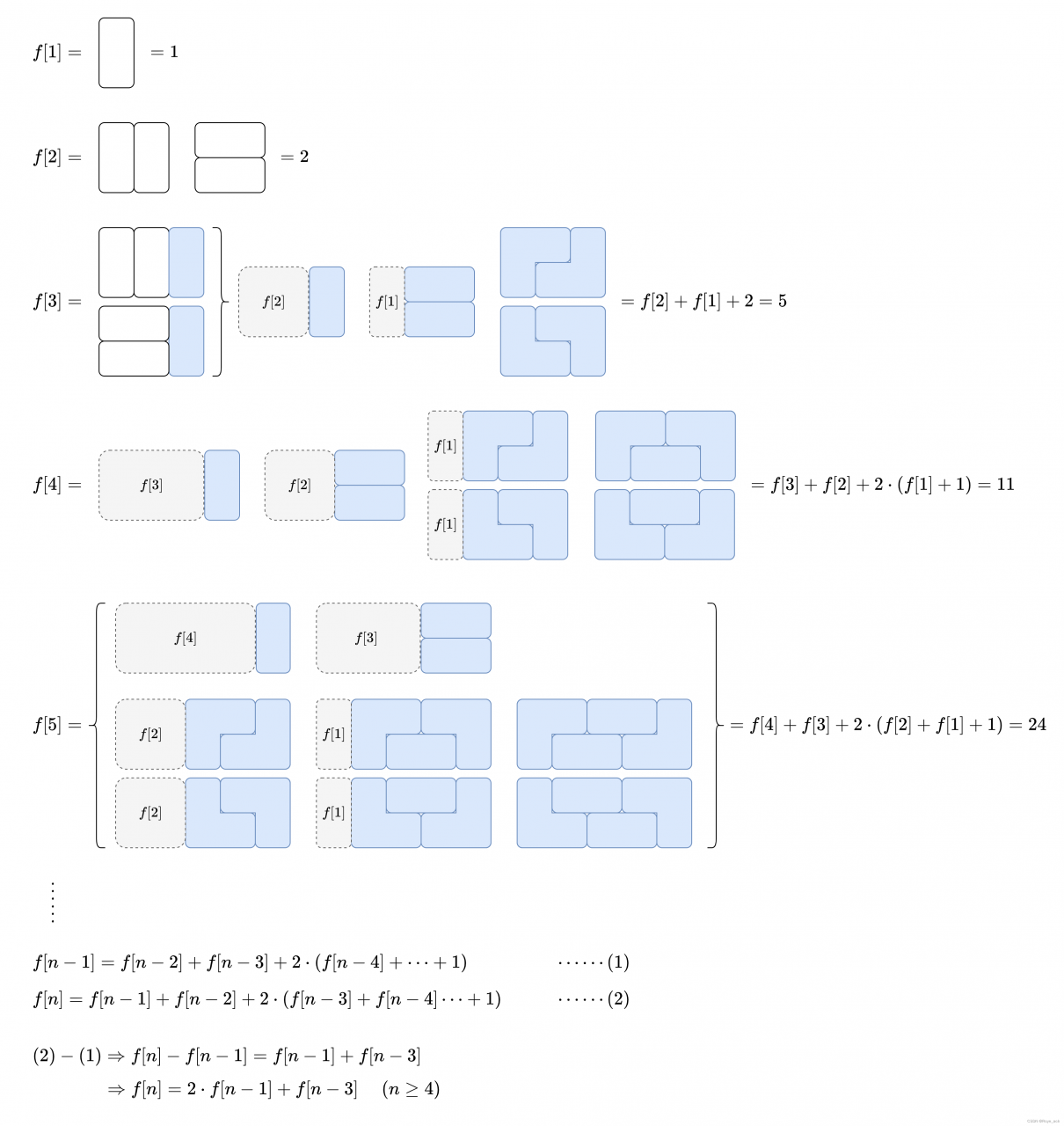
1、找规律dp

import java.util.*;

class Main
{
    static int N=10000010;
    static int mod=1000000007;
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        long[] dp=new long[N];
        dp[1]=dp[0]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++) dp[i]=(dp[i-1]*2+dp[i-3])%mod;
        System.out.print(dp[n]);
    }
}

2、状态压缩DP

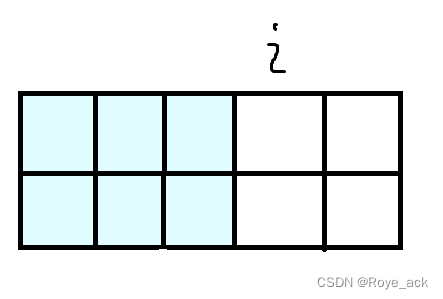
定义  为已经摆好前i-1列(前i-1列不留空)，且第i列状态为j的方案数

• j=0时，表示第i列上下均未摆积木
• j=1时，表示下面摆了，上面没摆
• j=2时，表示上面摆了，下面没摆
• j=3时，表示上下均摆放

因此，答案为 

先考虑如何初始化

当n=0时，可以视为已经上下均摆的情况，

然后考虑如何进行状态转移

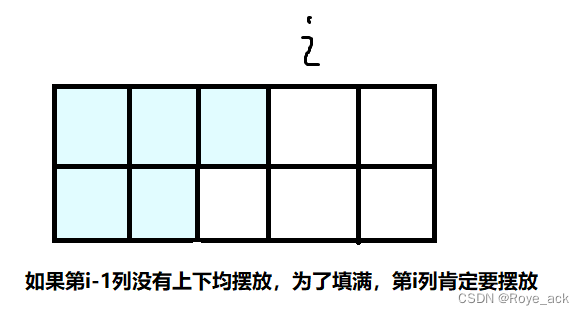
• 当j=0时，即第i列上下均未摆放，这种情况就要求第i-1列上下均摆好

 

 所以

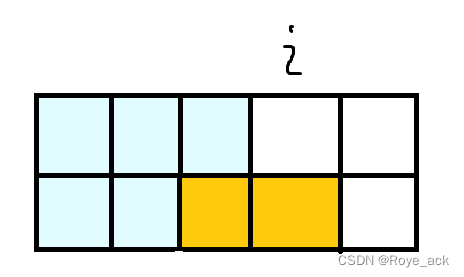
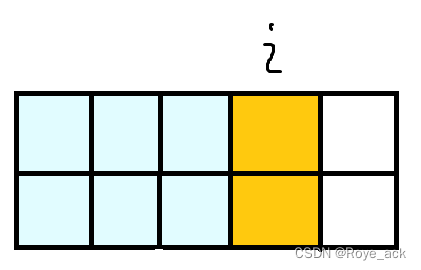
• 当j=1时，即第i列上面未摆，下面摆放，此时有两种情况：

第一种如下图： 

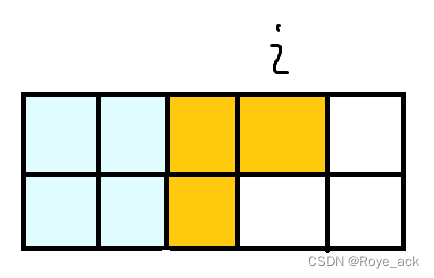
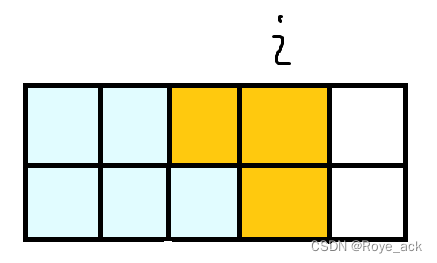
 第二种如下图：

 

 所以 

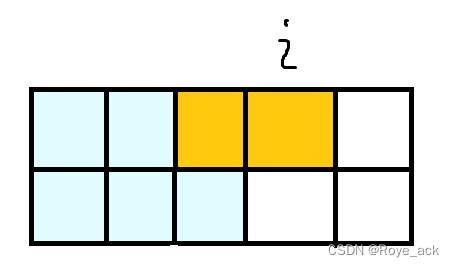
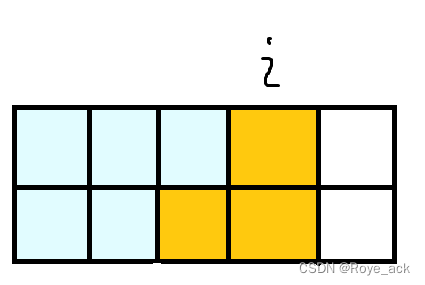
• 当j=2时，即上面摆了，下面没摆，此时也有两种情况

第一种如下图：

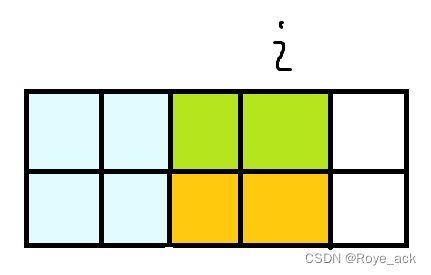
 第二种如下图：

 所以

• 当j=3时，即上下全摆，有四种情况：

第一种如下图：

第二种如下图：

 第三种如下图：

 第四种如下图：

 

所以

import java.util.*;

class Main
{
    static int N=10000010;
    static int mod=1000000007;
    static int[][] f=new int[N][4];
    
    public static void main(String[] args)
    {
        Scanner sc=new Scanner(System.in);
        int n=sc.nextInt();
        
        f[0][3]=1;
        for(int i=1;i<=n;i++) 
        {
            f[i][0]=f[i-1][3];
            f[i][1]=(f[i-1][0]+f[i-1][2])%mod;
            f[i][2]=(f[i-1][0]+f[i-1][1])%mod;
            f[i][3]=(((f[i-1][0]+f[i-1][1])%mod+f[i-1][2])%mod+f[i-1][3])%mod;
        }
        System.out.print(f[n][3]);
    }
}