AcWing—差分算法

差分算法是前缀和算法的逆运算。两者可以对比着学习：

一、什么是差分？

差分的概念是相对与前缀和说明的。

二、差分的作用

我们画图解释一下这里很容易出错：

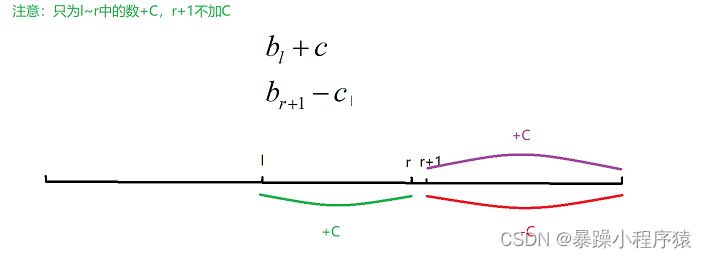
  我们从l开始都加了C，但是只是区间[l,r]上加C，所以我们从r+1开始就减去C，最后的结果是只有所选区间的每一个数增加了C。
  之前我们给所选区间每个数加C它的时间复杂度是O(n),使用差分算法之后时间复杂度可以提升到O(1),只需要修改下面两步即可：

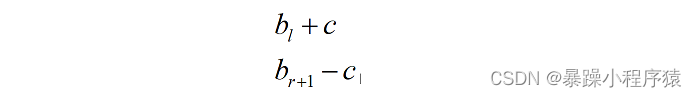
很对人都在考虑如何构造差分数组，其实不需要担心。
我们假设：

三、一维差分模板

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

四、二维差分

一维差分是在一段上插入C，而二维差分就是在一个子矩阵加上C，原理类似：

五、二维差分构造方法图示：

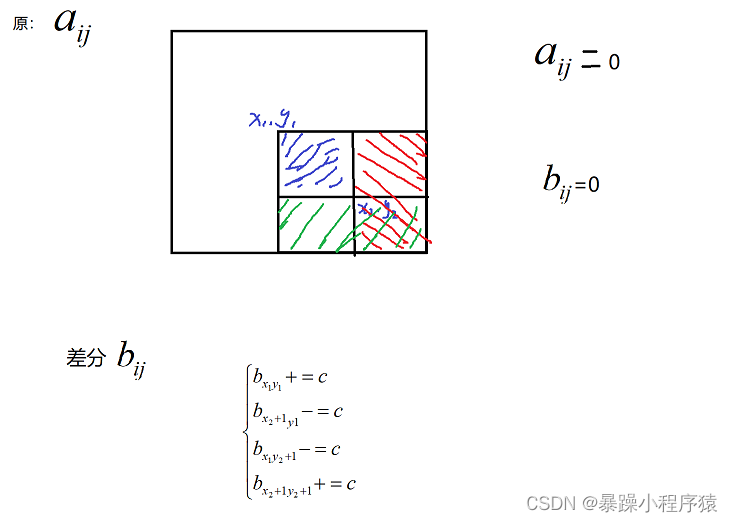
六、二维差分矩阵模板

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

总结

  今天分享了差分算法，这个算法可以和之前的前缀和算法比较着学习，这两个算法的关系很紧密，理解了其中一个另外一个也很容易理解，作用就是给所选区间中的每个数加上C，提高时间效率，使时间复杂度达到O(n),希望对大家有帮助，我们明天见~