题意：给出一颗二叉树的先序遍历和中序遍历,输出后续遍历序列。

样例输入输出：

输入：                                  输出 ：
DBACEGF ABCDEFG                         ACBFGED
BCAD CBAD                               CDAB

解题思路：

这道题的核心便是通过先序遍历和中序遍历先还原树的结构。

首先先了解什么是先序遍历，什么是中序遍历？不管是中序还是先序、后序。其实不同的便是节点遍历与遍历左右子树的顺序先后。

先序遍历：节点+左子树+右子树

中序遍历：左子树+节点+右子树

核心代码

node*rebuild(int p1,int p2,int in1,int in2)
{
	if(p1>p2||in1>in2)return NULL;//没有节点的时候返回 
	node*root=new node(pre[p1]);
	//先建立根节点
	int i=in1;
	for(i;i<in2;i++)
	{
		if(in[i]==pre[p1])break;
	} 
	//找到根节点在中序排序中的位置i,
	//[in1,i-1]为i节点的左子树，[i+1,in2]为i节点的右子树
	int num=i-in1;
	root->setLeft(rebuild(p1+1,p1+num,in1,i-1));
	//建立根节点root的左子树，
	//在先序遍历中左子树的范围为：p1+1,p1+num 
	//在中序遍历中右子树的范围为：in1,i-1 
	
	root->setRight(rebuild(p1+num+1,p2,i+1,in2));
	//建立根节点root的右子树
	//在先序遍历中右子树的范围为：p1+num+1,p2
	//在中序遍历中右子树的范围为：i+1，in2
	 
	return root;//返回 
}

图画展示

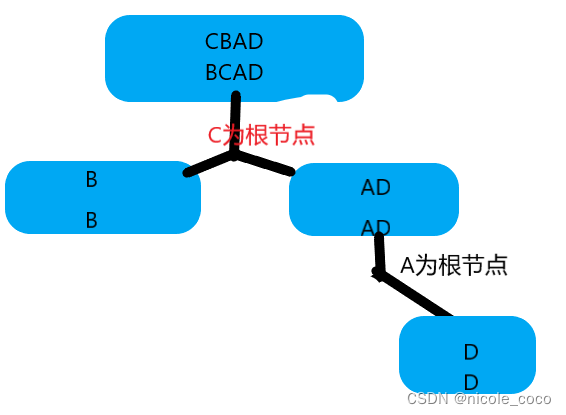
最后生成的树为：

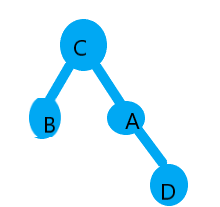
我尽力了，图片太难看，忍一下吧，😂

代码 

#include<iostream>
using namespace std;
struct node
{
	char data;//这是数据
	node*left;//左子节点 
	node*right;//这是右子节点
	node(char d='a',node*l=NULL,node*r=NULL)
	{
		data=d;left=l;right=r;
	}  
	void setLeft(node*l=NULL)//设置左子节点 
	{
		left=l;
	}
	void setRight(node*r=NULL)//设立右子节点 
	{
		right=r;
	}
};
string pre,in;
node*rebuild(int p1,int p2,int in1,int in2);//通过两个遍历重新构造树 
void postorder(node*root);//后序遍历 
void remove(node*root);//清空操作， 
int main()
{
	while(cin>>pre>>in)
	{
		int len=pre.length();
		node*root=rebuild(0,len-1,0,len-1);//重新构造树 
		postorder(root);//后序遍历 
		printf("\n");
		remove(root);//删除树 
	}
}
void remove(node*root)
{
	if(root==NULL)return;
	remove(root->left);
	remove(root->right);
	delete root;
}
void postorder(node*root)
{
	if(root==NULL)return;
	postorder(root->left);
	postorder(root->right);
	printf("%c",root->data);
	return;
}
node*rebuild(int p1,int p2,int in1,int in2)
{
	if(p1>p2||in1>in2)return NULL;//没有节点的时候返回 
	node*root=new node(pre[p1]);
	//先建立根节点
	int i=in1;
	for(i;i<in2;i++)
	{
		if(in[i]==pre[p1])break;
	} 
	//找到根节点在中序排序中的位置i,
	//[in1,i-1]为i节点的左子树，[i+1,in2]为i节点的右子树
	int num=i-in1;
	root->setLeft(rebuild(p1+1,p1+num,in1,i-1));
	//建立根节点root的左子树，
	//在先序遍历中左子树的范围为：p1+1,p1+num 
	//在中序遍历中右子树的范围为：in1,i-1 
	
	root->setRight(rebuild(p1+num+1,p2,i+1,in2));
	//建立根节点root的右子树
	//在先序遍历中右子树的范围为：p1+num+1,p2
	//在中序遍历中右子树的范围为：i+1，in2
	 
	return root;//返回 
}

 个人总结

这篇文章的图实在太丑，大家忍一下吧😂。

在这道题前面，其实紫书还有一道相似的题，UVA548，如果感觉自己掌握的小伙伴，可以去练习一下