部分内容引自百度百科
正态分布
由来:1805年勒让德计算彗星轨道时首次采用了最小二乘法,
高斯在1809年时在写<<天体运动理论>>,然后发现其计算过程中会出现误差,在求误差的过程中发现其误差呈正态分布(Normal distribution),又称高斯分布(Gaussian distribution),并用最小二乘法去验证
假设误差的密度函数为f(x),有n个独立观测值,x1…xn,真实值为x
正常来讲,大部分的误差都是在标准范围内进行变动的,
于是,为了表示误差,就能构造一个函数L(x)
L(x) = f(x1-x)…f(xn – x)
两边取对数(这一步,是为了拉开距离)
ln L(x) = ln (f(x1-x)…f(xn – x))
进一步,为了让其达到最大值的状态,我们想到了一个找函数变化率的工具,导数,然后考虑到里面有多个未知数,我们对它求偏导,
下图中因为等号的另一端为0,故前面的负号是可以去掉的

为了方便表示,我们记g(x) = f’(x)/f(x)
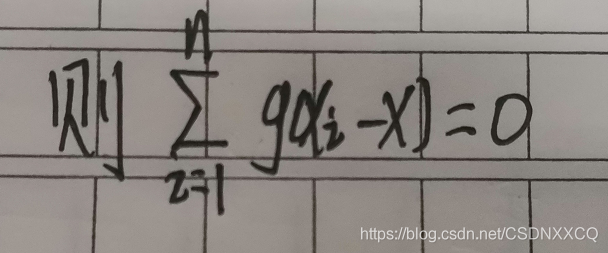
高斯认为,真实值x的估计为x拔
对x1求偏导
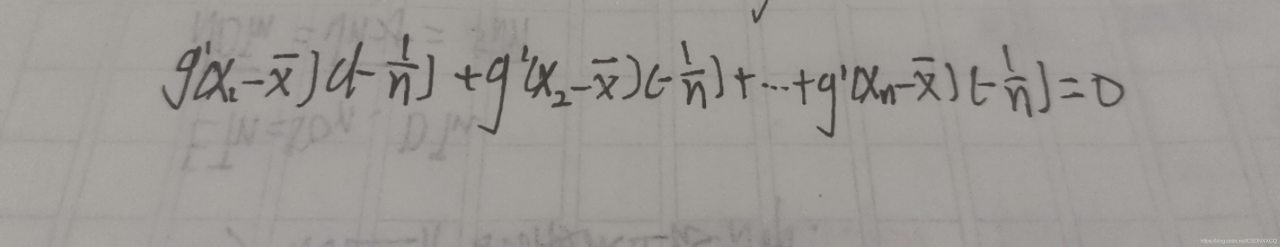
对x2求偏导
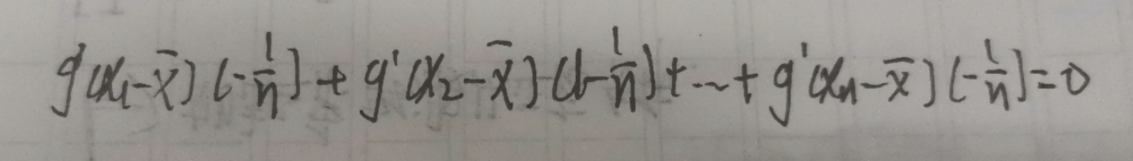
以此类推,到Xn

将这些其次线性方程组,写成矩阵(其秩为n-1,只有一个自由变量),并利用其次线性方程组的性质求解,得
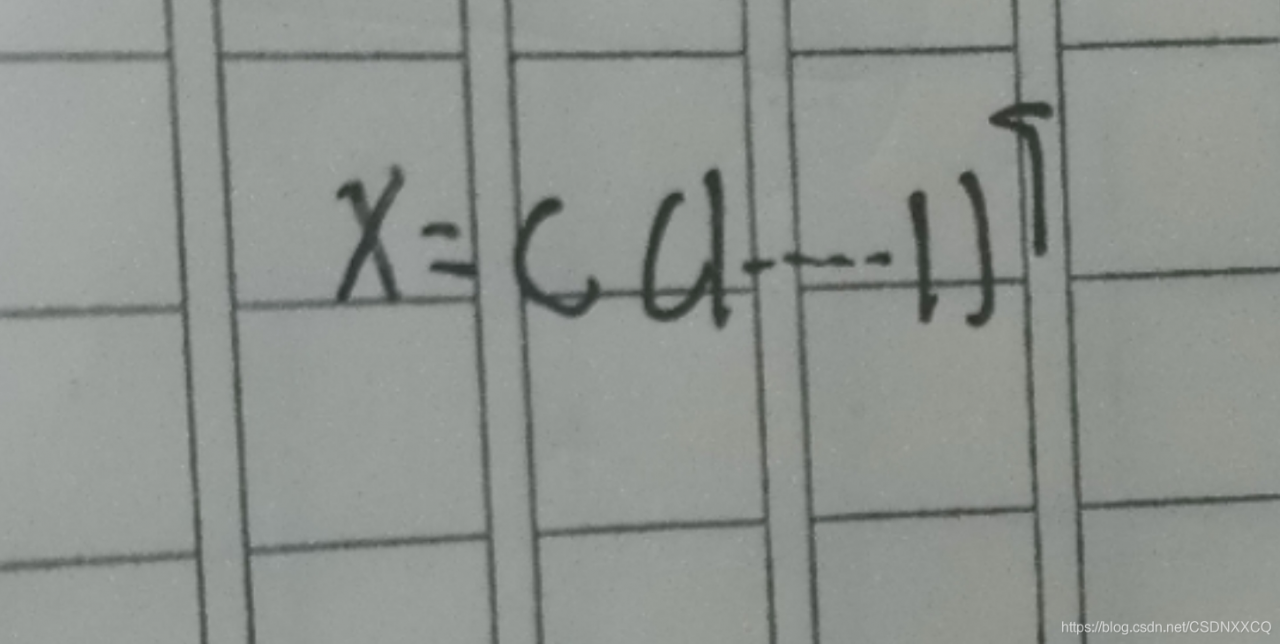
即
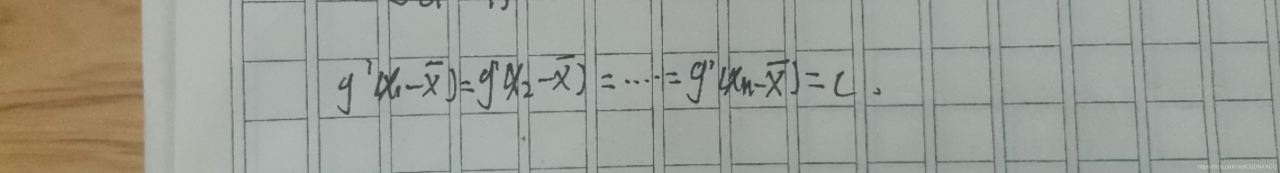
则
g(x) = cx+b
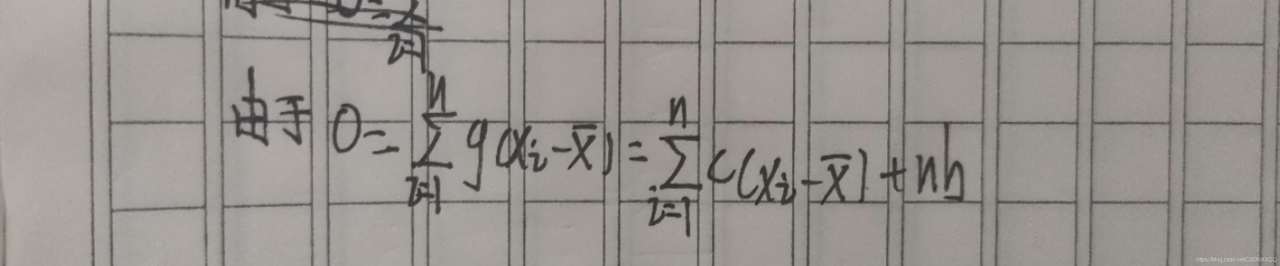
故c后面括号内的数值为0
故b=0
f’(x)/f(x)= cx拔
解这个微分方程,得
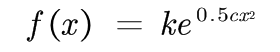
由于
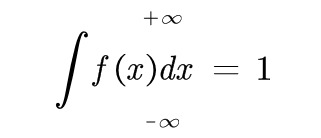
故
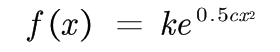
这个函数总体是收敛得,那么,常数c应该为负数
我们记c = -1/σ^2
进一步,利用二重积分求解
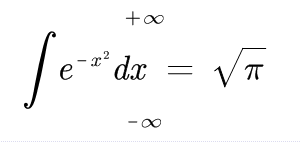
然后对比
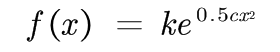
将k求出
![]() ~(0,σ^2)
~(0,σ^2)
相关补充
依概率收敛
百度百科的定义

理解:
设X = 预测值与真实值得距离趋近于0
在第无穷个预测值x1时
P(x1) = 1(注意,这是吧这个预测值与真实值得距离看成了一个事件,故p指的是概率)
![]()
根据对立事件的原则,也可以写为
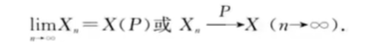
大数定律
切比雪夫大数定律
伯努利大数定律
辛钦大数定律



切比雪夫大数定律和辛钦大数定律其实是一样的,写法不同而已
大数定律告诉我们,在满足一定的条件下,所有的大数定律均为
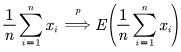
随机变量收敛到一个数里,说的就是大数定律是在体现随机变量均值的稳定性
(均值在大样本的情况下是趋于稳定的)
中心极限定理

在满足一定的条件下,中心极限定理均为
如果xi独立同分布于一个分布
则
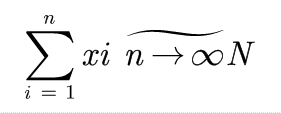
即x的和服从正态分布
且(转化为标准正态分布)
且
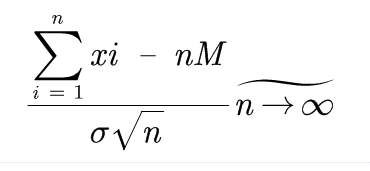
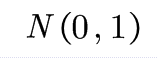
林德伯格-列维定理
林德伯格-列维 [1] (Lindburg-Levy)定理,即独立同分布随机变量序列的中心极限定理。它表明,独立同分布、且数学期望和方差有限的随机变量序列的标准化和以标准正态分布为极限。
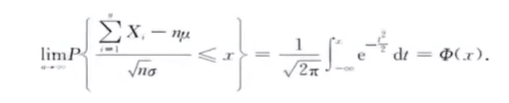
设随机变量X1,X2,…Xn,…相互独立,服从同一指数分布,且具有数学期望和方差:E(Xk)=μ,D(Xk)=σ^2>0(k=1,2…),则随机变量之和的标准化变量的分布函数Fn(x)对于任意x满足limFn(x)=Φ(x) 其中Φ(x)是标准正态分布的分布函数