D=(2,3,1,3,4,5,2);P(15,12,11,10,8,5,4);
首先将作业按p1≥p2 ≥ … ≥ pn排序, 将作业1存入解数组J中, 然后按照如下步骤逐一处理作业2到作业n;假设已处理完了i-1个作业, 其中有k个作业可构成可行解,已存入J(1),J(2)…J(k)中, 且D(J(1))<=D(J(2)) <=…<=D(J(k))
§现在处理作业i, 判断Jυ{i}是否可行, 就是看是否能为其中作业都找到适当插入位置r, 使作业i插入后有D(J(r))≥r; 1≤r≤k+1. 过程如下:
将D(J(k)), D(J(k-1)),…依次与D(i)比较,若D(J(l))>D(i)且D(J(l))≠l,l≤k,则作业J(l)可以向后延迟一个单位时间来处理,作业i可以在J(l)之前处理。


1 package greedy; 2 3 public class JS { 4 int n=7; 5 int [] D={0,2,3,1,3,4,5,2};//下标从1开始 6 float[] P={0,15,12,11,10,8,5,4};//先对P进行非增排序 7 int[] J=new int[n+1]; 8 int k; 9 JS(){ 10 k=js(D,J,n,k); 11 System.out.println("可调度作业数目:"+k); 12 double sum=0; 13 System.out.print("作业调度次序:"); 14 for(int i=1;i<=k;i++){ 15 System.out.print("->"+J[i]); 16 sum+=P[J[i]]; 17 } 18 System.out.println(); 19 System.out.println("总收益Sum="+sum); 20 } 21 public int js(int[] D,int[] J,int n,int k){ 22 int i,r; 23 k=1; 24 J[1]=1;//把第一个作业加入 25 for(i=2;i<n;i++){ 26 r=k; 27 while(D[J[r]]>D[i]&&D[J[r]]!=r){ 28 r--; 29 } 30 if(D[J[r]]<=D[i]&&D[i]>r){ 31 for(int l=k;l>r;l--){ 32 J[l+1]=J[l]; 33 } 34 J[r+1]=i; 35 k++; 36 } 37 } 38 return k; 39 } 40 public static void main(String[] args) { 41 // TODO Auto-generated method stub 42 new JS(); 43 } 44 45 }
View Code
测试结果:
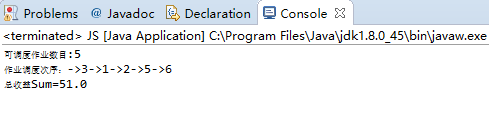
转载于:https://www.cnblogs.com/yuanzhenliu/p/5133168.html