原文出自:http://blog.csdn.net/pirage/article/details/9851339
最近一直在做相关推荐方面的研究与应用工作,召回率与准确率这两个概念偶尔会遇到,
知道意思,但是有时候要很清晰地向同学介绍则有点转不过弯来。
召回率和准确率是数据挖掘中预测、互联网中的搜索引擎等经常涉及的两个概念和指标。
召回率:Recall,又称“查全率”——还是查全率好记,也更能体现其实质意义。
准确率:Precision,又称“精度”、“正确率”。
以检索为例,可以把搜索情况用下图表示:
|
相关
|
不相关
|
|
|
检索到
|
A
|
B
|
|
未检索到
|
C
|
D
|
A:检索到的,相关的 (搜到的也想要的)
B:检索到的,但是不相关的 (搜到的但没用的)
C:未检索到的,但却是相关的 (没搜到,然而实际上想要的)
D:未检索到的,也不相关的 (没搜到也没用的)
如果我们希望:被检索到的内容越多越好,这是追求“查全率”,即A/(A+C),越大越好。
如果我们希望:检索到的文档中,真正想要的、也就是相关的越多越好,不相关的越少越好,
这是追求“准确率”,即A/(A+B),越大越好。
“召回率”与“准确率”虽然没有必然的关系(从上面公式中可以看到),在实际应用中,是相互制约的。
要根据实际需求,找到一个平衡点。
往往难以迅速反应的是“召回率”。我想这与字面意思也有关系,从“召回”的字面意思不能直接看到其意义。
“召回”在中文的意思是:把xx调回来。“召回率”对应的英文“recall”,
recall除了有上面说到的“order sth to return”的意思之外,还有“remember”的意思。
Recall:the ability to remember sth. that you have learned or sth. that has happened in the past.
当我们问检索系统某一件事的所有细节时(输入检索query查询词),
Recall指:检索系统能“回忆”起那些事的多少细节,通俗来讲就是“回忆的能力”。
“能回忆起来的细节数” 除以 “系统知道这件事的所有细节”,就是“记忆率”,
也就是recall——召回率。简单的,也可以理解为查全率。
根据自己的知识总结的,定义应该肯定对了,在某些表述方面可能有错误的地方。
假设原始样本中有两类,其中:
1:总共有 P个类别为1的样本,假设类别1为正例。
2:总共有N个类别为0 的样本,假设类别0为负例。
经过分类后:
3:有 TP个类别为1 的样本被系统正确判定为类别1,FN 个类别为1 的样本被系统误判定为类别 0,
显然有P=TP+FN;
4:有 FP 个类别为0 的样本被系统误判断定为类别1,TN 个类别为0 的样本被系统正确判为类别 0,
显然有N=FP+TN;
那么:
精确度(Precision):
P = TP/(TP+FP) ; 反映了被分类器判定的正例中真正的正例样本的比重(
准确率(Accuracy)
A = (TP + TN)/(P+N) = (TP + TN)/(TP + FN + FP + TN);
反映了分类器统对整个样本的判定能力——能将正的判定为正,负的判定为负
召回率(Recall),也称为 True Positive Rate:
R = TP/(TP+FN) = 1 – FN/T; 反映了被正确判定的正例占总的正例的比重
转移性(Specificity,不知道这个翻译对不对,这个指标用的也不多),
也称为 True NegativeRate
S = TN/(TN + FP) = 1 – FP/N; 明显的这个和召回率是对应的指标,
只是用它在衡量类别0 的判定能力。
F-measure or balanced F-score
F = 2 * 召回率 * 准确率/ (召回率+准确率);这就是传统上通常说的F1 measure,
另外还有一些别的F measure,可以参考下面的链接
上面这些介绍可以参考:
http://en.wikipedia.org/wiki/Precision_and_recall
同时,也可以看看:http://en.wikipedia.org/wiki/Accuracy_and_precision
为什么会有这么多指标呢?
这是因为模式分类和机器学习的需要。判断一个分类器对所用样本的分类能力或者在不同的应用场合时,
需要有不同的指标。 当总共有个100 个样本(P+N=100)时,假如只有一个正例(P=1),
那么只考虑精确度的话,不需要进行任何模型的训练,直接将所有测试样本判为正例,
那么 A 能达到 99%,非常高了,但这并没有反映出模型真正的能力。另外在统计信号分析中,
对不同类的判断结果的错误的惩罚是不一样的。举例而言,雷达收到100个来袭 导弹的信号,
其中只有 3个是真正的导弹信号,其余 97 个是敌方模拟的导弹信号。假如系统判断 98 个
(97 个模拟信号加一个真正的导弹信号)信号都是模拟信号,那么Accuracy=98%,
很高了,剩下两个是导弹信号,被截掉,这时Recall=2/3=66.67%,
Precision=2/2=100%,Precision也很高。但剩下的那颗导弹就会造成灾害。
因此在统计信号分析中,有另外两个指标来衡量分类器错误判断的后果:
漏警概率(Missing Alarm)
MA = FN/(TP + FN) = 1 – TP/T = 1 – R; 反映有多少个正例被漏判了
(我们这里就是真正的导弹信号被判断为模拟信号,可见MA此时为 33.33%,太高了)
虚警概率(False Alarm)
FA = FP / (TP + FP) = 1 – P;反映被判为正例样本中,有多少个是负例。
统计信号分析中,希望上述的两个错误概率尽量小。而对分类器的总的惩罚旧
是上面两种错误分别加上惩罚因子的和:COST = Cma *MA + Cfa * FA。
不同的场合、需要下,对不同的错误的惩罚也不一样的。像这里,我们自然希望对漏警的惩罚大,
因此它的惩罚因子 Cma 要大些。
个人观点:虽然上述指标之间可以互相转换,但在模式分类中,
一般用 P、R、A 三个指标,不用MA和 FA。而且统计信号分析中,也很少看到用 R 的。
好吧,其实我也不是IR专家,但是我喜欢IR,最近几年国内这方面研究的人挺多的,google和百度的强势,也说明了这个方向的价值。当然,如果你是学IR的,不用看我写的这些基础的东西咯。如果你是初学者或者是其他学科的,正想了解这些科普性质的知识,那么我这段时间要写的这个“信息检索X科普“系列也许可以帮助你。(我可能写的不是很快,见谅)
至于为什么名字中间带一个字母X呢? 
为什么先讲Precision和Recall呢?因为IR中很多算法的评估都用到Precision和Recall来评估好坏。所以我先讲什么是“好人“,再告诉你他是“好人“
查准与召回(Precision & Recall)
先看下面这张图来理解了,后面再具体分析。下面用P代表Precision,R代表Recall
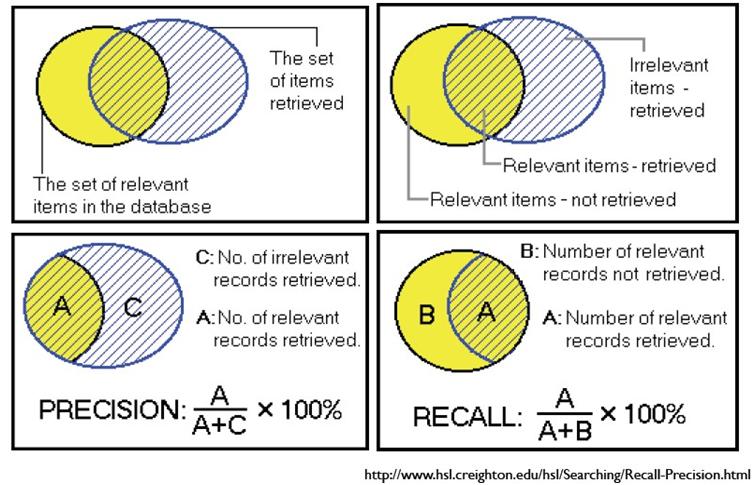
通俗的讲,Precision 就是检索出来的条目中(比如网页)有多少是准确的,Recall就是所有准确的条目有多少被检索出来了。
下面这张图介绍True Positive,False Negative等常见的概念,P和R也往往和它们联系起来。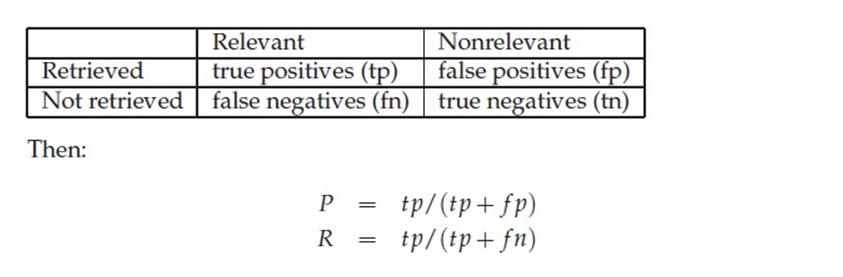
我们当然希望检索的结果P越高越好,R也越高越好,但事实上这两者在某些情况下是矛盾的。比如极端情况下,我们只搜出了一个结果,且是准确的,那么P就是100%,但是R就很低;而如果我们把所有结果都返回,那么必然R是100%,但是P很低。
因此在不同的场合中需要自己判断希望P比较高还是R比较高。如果是做实验研究,可以绘制Precision-Recall曲线来帮助分析(我应该会在以后介绍)。
F1 Measure
前面已经讲了,P和R指标有的时候是矛盾的,那么有没有办法综合考虑他们呢?我想方法肯定是有很多的,最常见的方法应该就是F Measure了,有些地方也叫做F Score,都是一样的。
F Measure是Precision和Recall加权调和平均:
F = (a^2+1)P*R / a^2P +R
当参数a=1时,就是最常见的F1了:
F1 = 2P*R / (P+R)
很容易理解,F1综合了P和R的结果。