文章目录
1. 矩的概念介绍
图像识别的一个核心问题是图像的特征提取,简单描述即为用一组简单的数据(数据描述量)来描述整个图像,这组数据月简单越有代表性越好。良好的特征不受光线、噪点、几何形变的干扰,图像识别技术的发展中,不断有新的描述图像特征提出,而图像不变矩就是其中一个。
从图像中计算出来的矩通常描述了图像不同种类的几何特征如:大小、灰度、方向、形状等,图像矩广泛应用于模式识别、目标分类、目标识别与防伪估计、图像编码与重构等领域。
严格来讲矩是概率与统计中的一个概念,是随机变量的一种数字特征。设 xx 为随机变量,C为常数,则量E[(x−c)^k]称为X关于C点的k阶矩。比较重要的两种情况如下:
-
c=0,这时a_k=E(X^k)称为X的k阶原点矩;
-
c=E(X),这时μ_k=E[(X−EX)^k]称为X的k阶中心矩
一阶原点矩就是期望,一阶中心矩μ_1=0,二阶中心矩μ_2就是X的方差Var(X)。在统计学上,高于4阶的矩极少使用,μ_3可以去衡量分布是否有偏,μ_4可以衡量分布(密度)在均值拘谨的陡峭程度。
针对一幅图像,我们把像素的坐标看成是一个二维随机变量(X, Y),那么一副灰度图可以用二维灰度图密度函数来表示,因此可以用矩来描述灰度图像的特征。
不变矩(Invariant Moments)是一种高度浓缩的图像特征,具有平移、灰度、尺度、旋转不变性,由M.K.Hu在1961年首先提出,1979年M.R.Teague根据正交多项式理论提出了Zernike矩
opencv中提供的API用来计算中心矩和Hu矩。
1.1 图像矩相关公式
- 几何矩
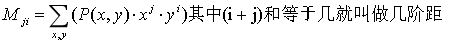
- 中心矩
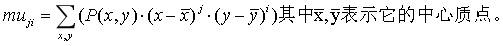
- 中心归一化矩
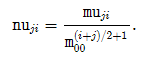
- 图像中心Center(x0, y0)
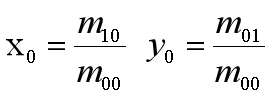
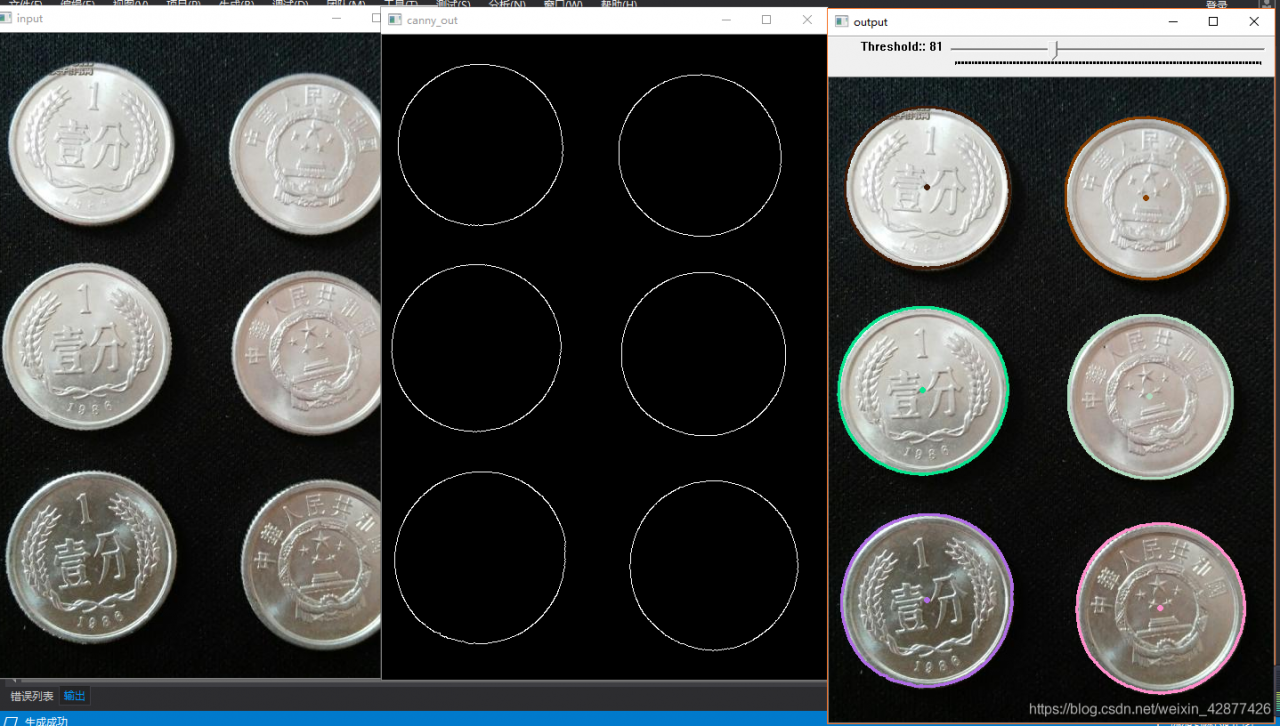
2. 步骤
- 提取图像边缘
- 发现轮廓
- 计算每个轮廓对象的矩
- 计算每个对象的中心、弧长、面积
3. 相关API
opencv中提供了moments()来计算图像中的中心矩(最高到三阶),HuMoments()用于由中心矩计算Hu矩.同时配合函数contourArea函数计算轮廓面积和arcLength来计算轮廓或曲线长度。
3.1 计算中心矩cv::moments()
- 计算图像中的中心矩(最高到三阶)
moments(
InputArray array,//输入数据,可以是光栅图像(单通道,8-bit或浮点型二维数组),或者是一个二维数组(1 X N或N X 1),二维数组类型为Point或Point2f。
bool binaryImage=false // 是否为二值图像,默认值是false,如果为true,则所有非零的像素都会按值1对待,也就是说相当于对图像进行了二值化处理,阈值为1,此参数仅对图像有效。
)
3.2 contourArea()
contourArea(
InputArray contour,//输入轮廓数据,是一个向量,二维点,可以是vector或Mat类型
bool oriented// 默认false, 如果为true,该函数返回一个带符号的面积,其正负取决于轮廓的方向(顺时针还是逆时针)。根据这个特性可以根据面积的符号来确定轮廓的位置。如果是默认值false,则面积以绝对值的形式返回.
- 该函数使用Green formula计算轮廓面积,返回面积和非零像素数量如果使用drawContours或fillPoly绘制轮廓,可能导致不同。
3.3 arcLength()
- 计算轮廓或曲线长度。
arcLength(
InputArray curve,//输入曲线数据,输入二维点集,可以是vector或Mat类型
bool closed// 是否是封闭曲线
4. 例程
#include<opencv2/opencv.hpp>
#include<iostream>
#include<math.h>
using namespace cv;
using namespace std;
Mat blured;
Mat src, dst;
RNG rng(12345);
int Threshold=81;
void CallBack(int, void*);
int main() {
src = imread("D:/resource/images/硬币.jpg");
if (src.empty()) {
printf("the image couldn't be loaded...");
return -1;
}
imshow("input", src);
GaussianBlur(src, blured, Size(21, 21), 0);
namedWindow("output");
createTrackbar("Threshold:", "output", &Threshold, 255, CallBack);
CallBack(0, 0);
waitKey(0);
return -1;
}
void CallBack(int, void*) {
//提取边缘
Mat canny_out;
Canny(blured, canny_out, Threshold, Threshold * 2);
imshow("canny_out", canny_out);
vector<vector<Point>> contours;
findContours(canny_out, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE,Point(0,0));
vector<Moments> contours_moments(contours.size());//图像的中心矩
vector<Point2f> ccs(contours.size());//图像中心坐标
for (size_t i = 0; i < contours.size(); i++) {
//提取各图像的中心矩和中心坐标
contours_moments[i] = moments(contours[i]);
ccs[i] = Point(static_cast<float>(contours_moments[i].m10 / contours_moments[i].m00), static_cast<float>(contours_moments[i].m01 / contours_moments[i].m00));
//绘制边缘和各图像中心
Scalar color = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255));
drawContours(src, contours, i, color, 2, 8);
circle(src, ccs[i], 2, color, 2, 8);
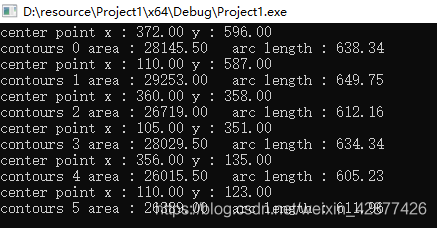
//打印各图像中心坐标,面积和边缘长度
printf("center point x : %.2f y : %.2f\n", ccs[i].x, ccs[i].y);
printf("contours %d area : %.2f arc length : %.2f\n", i, contourArea(contours[i]), arcLength(contours[i], true));
}
imshow("output", src);
return;
}