网络流

流网络：

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)是一个有向图，网络中有两个特殊点：源点s与汇点t。容量用

c

c

c表示，流量用

f

f

f表示

流网络G中满足两个性质：1、容量限制(通过一条边的流量不会超过该边的容量)，2、流量守恒(从源点s流出的量=最终到达汇点t的量；除了源点s和汇点t外，流入一个点的量=流出一个点的量)

因为不考虑负流量，所以对于

∀

u

,

v

ε

V

,

f

(

u

,

v

)

=

f

(

v

,

u

)

\forall u,v \varepsilon V, f(u,v)=f(v,u)

∀u,vεV,f(u,v)=f(v,u)

称

f

(

u

,

v

)

f(u,v)

f(u,v)为从

u

u

u到

v

v

v的流，流

f

f

f的值定义为：

∣

f

∣

=

∑

v

ε

V

f

(

s

,

v

)

|f|=\sum_{v \varepsilon V}{f(s,v)}

∣f∣=vεV∑​f(s,v)
对于流网络

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)，设流

f

f

f为

G

G

G中的流。对于

G

G

G中的每条边

<

u

,

v

>

ε

E

<u,v> \varepsilon E

<u,v>εE，可以定义残留容量为在不超过容量限制的条件下，可以通过的额外的网络流量：

c

f

(

u

,

v

)

=

c

(

u

,

v

)

−

f

(

u

,

v

)

c_{f}(u,v)=c(u,v)-f(u,v)

cf​(u,v)=c(u,v)−f(u,v)
残留网络依然是一个流网络，容量由

c

f

c_{f}

cf​给出。设

f

f

f是流网络

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)中的一个流，

f

′

f’

f′是其残留网络

G

f

G_{f}

Gf​的一个流，则

f

+

f

′

f+f’

f+f′仍是网络

G

G

G的一个流。

增广路径：指的是残留网络

G

f

G_{f}

Gf​上源点

s

s

s到汇点

t

t

t的一条简单路径，该路径的残留容量为可以沿该路径增加的最多额外流量

c

f

(

p

)

=

m

i

n

{

c

f

(

u

,

v

)

∣

<

u

,

v

>

ε

p

}

c_{f}(p)=min\{c_{f}(u,v)|<u,v> \varepsilon p\}

cf​(p)=min{cf​(u,v)∣<u,v>εp}

c

f

(

p

)

>

0

c_{f}(p)>0

cf​(p)>0。

所以在残留网络中满足

c

f

(

u

,

v

)

=

{

c

(

u

,

v

)

−

f

(

u

,

v

)

,

(u,v) 

ε

 E

f

(

v

,

u

)

,

(v,u) 

ε

 E

c_{f}(u,v)= \begin{cases} c(u,v)-f(u,v), & \text{(u,v) $\varepsilon$ E} \\ f(v,u), & \text{(v,u) $\varepsilon$ E} \end{cases}

cf​(u,v)={c(u,v)−f(u,v),f(v,u),​(u,v) ε E(v,u) ε E​
意思就是残留网络分为两种边，一种是原图中的边，

c

f

(

u

,

v

)

c_{f}(u,v)

cf​(u,v)就是表示这条边还能再流过多少流量，另一种是原图中的边的反向边，

c

f

(

u

,

v

)

c_{f}(u,v)

cf​(u,v)就是表示通过反向边能往回退多少流量

例：

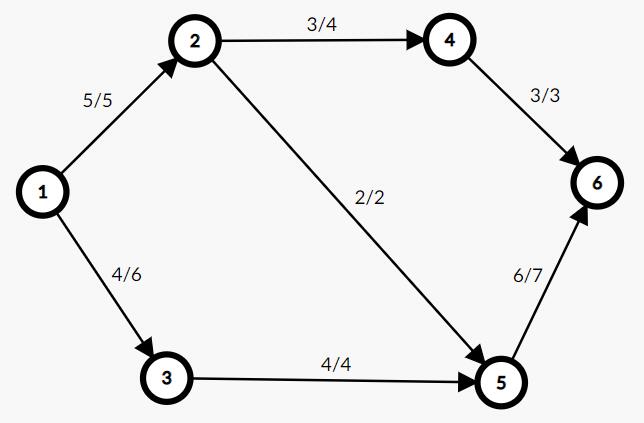
上图为原图中每条边流量/容量

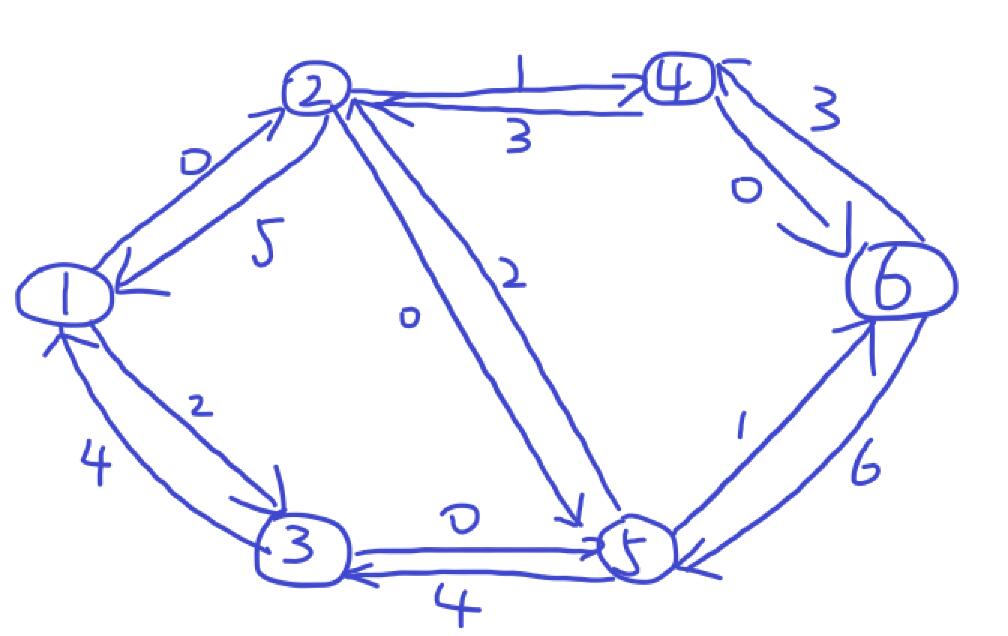
上图为残留网络中正向边和反向边容量的情况。通过增广路径的定义，我们可知无法从残留网络中找到一条可以从源点s走到汇点t并且边的容量大于0的路径

一个网络中的最大流也称为最大可行流。

流网络

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)的割

[

S

,

T

]

[S,T]

[S,T]将点集

V

V

V划分为

S

S

S和

T

(

T

=

V

−

S

)

T(T=V-S)

T(T=V−S)两部分，使得源点

s

ε

S

s \varepsilon S

sεS且汇点

t

ε

T

t \varepsilon T

tεT。符号

[

S

,

T

]

[S,T]

[S,T]代表一个边集合

{

<

u

,

v

>

∣

<

u

,

v

>

ε

E

,

u

ε

S

,

v

ε

T

}

\{<u,v>|<u,v> \varepsilon E,u \varepsilon S,v \varepsilon T\}

{<u,v>∣<u,v>εE,uεS,vεT}。穿过割

[

S

,

T

]

[S,T]

[S,T]的流量定义为

f

(

S

,

T

)

f(S,T)

f(S,T),割

[

S

,

T

]

[S,T]

[S,T]的容量定义为

c

(

S

,

T

)

c(S,T)

c(S,T)。

割的容量：

c

(

S

,

T

)

=

∑

u

ε

S

∑

v

ε

T

c

(

u

,

v

)

割的流量：

f

(

S

,

T

)

=

∑

u

ε

S

∑

v

ε

T

f

(

u

,

v

)

−

∑

u

ε

T

∑

v

ε

S

f

(

u

,

v

)

割的容量：c(S,T)=\sum_{u \varepsilon S}\sum_{v \varepsilon T}c(u,v)\\ 割的流量：f(S,T)=\sum_{u \varepsilon S}\sum_{v \varepsilon T}f(u,v) – \sum_{u \varepsilon T}\sum_{v \varepsilon S}f(u,v)

割的容量：c(S,T)=uεS∑​vεT∑​c(u,v)割的流量：f(S,T)=uεS∑​vεT∑​f(u,v)−uεT∑​vεS∑​f(u,v)
一个网络的最小割也就是该网络中容量最小的割。

割与流的关系：在一个流网络

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)中，设其任意一个流为

f

f

f，且

[

S

,

T

]

[S,T]

[S,T]为

G

G

G的一个割，则通过割的流量为

f

(

S

,

T

)

=

∣

f

∣

f(S,T)=|f|

f(S,T)=∣f∣。(从源点s流出的流量=流入汇点t的流量，所有流量一定通过某些边流过去)

推论:在一个流网络

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)中，设其任意一个流为

f

f

f,任意一个割为

[

S

,

T

]

[S,T]

[S,T],必有

∣

f

∣

≤

c

[

S

,

T

]

|f| \leq c[S,T]

∣f∣≤c[S,T]。

最大流最小割定理：如果

f

f

f是具有源点s和汇点t的流网络

G

=

(

V

,

E

)

G=(V,E)

G=(V,E)中的一个流，则下列条件是等价的：

(

1

)

f

是

G

的一个最大流

(

2

)

残留网络

G

f

不包含增广路径

(

3

)

对

G

的某个割

[

S

,

T

]

,

有

∣

f

∣

=

c

[

S

,

T

]

(1)\quad f是G的一个最大流\\ (2)\quad 残留网络G_{f}不包含增广路径\\ (3)\quad 对G的某个割[S,T],有|f|=c[S,T]

(1)f是G的一个最大流(2)残留网络Gf​不包含增广路径(3)对G的某个割[S,T],有∣f∣=c[S,T]
在求最大流算法中时间复杂度均为上限，与实际差距较大，可以简单认为EK算法可以求解点+边的和为

1

0

3

−

1

0

4

10^{3}-10^{4}

103−104大小的数据量，Dinic算法可以求解点+边的和为

1

0

4

−

1

0

5

10^{4}-10^{5}

104−105大小的数据量，求最大流时，EK算法和Dinic算法维护的都是残留网络。网络流问题的题目关键在于如何建图，怎么求只需要拉板子即可。

EK算法

时间复杂度上限

O

(

n

m

2

)

O(nm^{2})

O(nm2)

算法步骤：1、找增广路，2、更新残留网络(

G

f

−

>

G

f

+

f

′

G_{f}->G_{f+f’}

Gf​−>Gf+f′​)，一直到找不到增广路为止

更新残留网络：若正向边容量为

c

1

c_{1}

c1​，反向边容量为

c

2

c_{2}

c2​，假如多流了

k

k

k,所以正向边容量为

c

1

−

k

c_{1}-k

c1​−k，反向边容量为

c

2

+

k

c_{2}+k

c2​+k。

用邻接表的好处就是，如果边的下标从0开始，根据二进制运算的性质，它的反向边^1=它的正向边.

模板题

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int n, m, s, t;
int head[210], e[10010], ne[10010], idx, pre[210];
LL f[10010], w[210];
//f记录的是容量
//w数组是指从源点s开始走到第i点路径上所有边的容量的最小值
bool vis[210];
void add(int u, int v, int c) {
    //正向边
    e[idx] = v;
    f[idx] = c;
    ne[idx] = head[u];
    head[u] = idx++;
	//反向边
    e[idx] = u;
    f[idx] = 0;
    ne[idx] = head[v];
    head[v] = idx++;
}
bool bfs() {
    memset(vis, false, sizeof(vis));
    queue<int> q;
    q.push(s);
    vis[s] = true;
    w[s] = 1e18;
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (!vis[v] && f[i]) {
                vis[v] = true;
                pre[v] = i;//前驱边
                w[v] = min(w[u], f[i]);//到当前结点的最小容量=min(上一个点的最小容量，当前边的容量)
                if (v == t) {
                    return true;
                }
                q.push(v);
            }
        }
    }
    return false;
}
LL EK() {
    LL ans = 0;
    while (bfs()) {
        //由于每次只走一条增广路的边，所以每次都要加上w[t]
        //表示每一条增广路上从源点s走到汇点t这条路径上边的容量的最小值
        ans += w[t];
        for (int i = t; i != s; i = e[pre[i] ^ 1]) {//下一个点是前驱边的反向边所到达的点
            //前驱边所到达的点对应的流量减
            f[pre[i]] -= w[t];
            //前驱边的反向边所到达的点对应的流量加
            f[pre[i] ^ 1] += w[t];
        }
    }
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m >> s >> t;
    memset(head, -1, sizeof(head));
    for (int i = 0; i < m; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        add(u, v, c);
    }
    cout << EK() << '\n';
    return 0;
}

Dinic算法

时间复杂度上限

O

(

n

2

m

)

O(n^2m)

O(n2m)

步骤：1、bfs->建立分层图，判断有没有增广路2、dfs->找出所有能增广的路径，因为dfs不回溯，所以时间复杂度不是指数级别

Dinic算法对各种优化非常敏感，需要谨慎优化，少加一个优化都可能会TLE

AC代码：

#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int n, m, s, t;
int e[10010], ne[10010], head[210], idx;
int d[210], cur[210];
LL f[10010], w[10010];
void add(int u, int v, int c) {
    e[idx] = v;
    f[idx] = c;
    ne[idx] = head[u];
    head[u] = idx++;
    e[idx] = u;
    f[idx] = 0;
    ne[idx] = head[v];
    head[v] = idx++;
}
bool bfs() {
    memset(d, -1, sizeof(d));
    queue<int> q;
    q.push(s);
    d[s] = 0;
    cur[s] = head[s];
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (int i = head[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (d[v] == -1 && f[i]) {
                //d[]建立分层图，强制把u的下一个点连到v上
                d[v] = d[u] + 1;
                //cur[]记录当前点应该从所有连出去的边的哪一条开始遍历
                //因为在dfs的时候会删掉分层图上的边且永远不会用到了
                cur[v] = head[v];
                if (v == t) {
                    return true;
                }
                q.push(v);
            }
        }
    }
    return false;
}
LL dfs(int u, LL limit) {
    if (u == t) {
        return limit;
    }
    LL flow = 0;
    for (int i = cur[u]; ~i && flow < limit; i = ne[i]) {
        int v = e[i];
        cur[u] = i;
        if (d[v] == d[u] + 1 && f[i]) {
            LL now = dfs(v, min(f[i], limit - flow));
            if (now == 0) {
                //说明v这个点已经流满了 以后绝对用不到了 所以从分层图上删掉
                d[v] = -1;
            }
            f[i] -= now;
            f[i ^ 1] += now;
            flow += now;
        }
    }
    return flow;
}
LL Dinic() {
    LL ans = 0, flow;
    while (bfs()) {//每一次尽可能多的建立分层图 找到增广路
        while (flow = dfs(s, 1e18)) {//每一次求得新的增广路的流量
            ans += flow;
        }
    }
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m >> s >> t;
    memset(head, -1, sizeof(head));
    for (int i = 0; i < m; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        add(u, v, c);
    }
    cout << Dinic() << '\n';
    return 0;
}