如前所述,一大部分控制系统随着增益K的增大而容易变得不稳定。如果系统已经闭环稳定了,知道稳定裕度(Stability Margin)是很有意义的。Margin的意思简单来说就是gap,英语中margin其中一个含义就是指某件事距离失败或者成功之间的距离 (an amount by which a thing is won or falls short.) 。
稳定裕度这个名词取得可以,裕度在这里指的距离系统不稳定的某个量变化的宽裕程度。两种衡量指标,幅值裕度和相位裕度。这两种相对稳定性的指标与系统的时域响应是有联系的,在本章先只介绍概念。
下面的讨论都针对最小相位系统 minimum phase system。Non-minimum phase system的结论并不相同。非最小相位系统可能随着K值的增大而趋向于稳定。
记不记得住有一些结论并不重要,但是两种margin的概念一定要理解,理解为什么需要计算这两个值,这两值的大小分别对系统性能意味着什么。
1.幅值裕度GM与相位裕度PM
幅值裕度(gain margin ,GM)在上一篇Nyquist稳定性的临界稳定时提到过了,也就是phase为-180度对应的Bode Plot的幅值距离0dB线的幅值差,也可以是根轨迹上两个K值之比,后者是一个临界稳定时虚轴上的K值。GM是可正可负的。
相位裕度(phase margin,PM)依旧是根据临界稳定的条件,当频率特性幅值满足
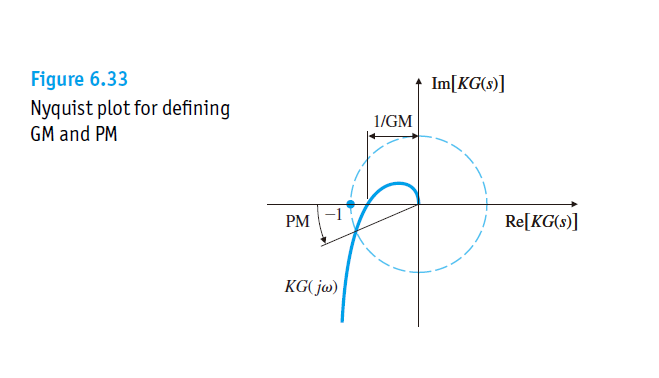
在Nyquist Plot上也可以去定义GM和PM。频率特性的相角如果为-180度时,那么对应的Nyquist Plot上曲线与负实部半轴的交点,此时交点幅值
意义为幅值再扩大GM倍后,则系统达到临界稳定,大于GM倍后系统不稳定。所以穿越频率时的交点幅值也就成为了1/GM。应该注意这个定义和Bode Plot的定义是一致的,因为在分贝单位下,GM的定义式子就变成了
所以也就等同于0dB线与
PM也类似,当幅值为1时,则曲线穿越单位圆,则是相角与-180之差定义为PM。下图中所示的为正PM,因为从正半轴顺时针开始计算,则从0往-180度角度是逐渐变小的,注意如果从正半轴逆时针开始计算,负半轴相角为180度,那么下图的PM的值就会大于180度,依旧是正的。我们以负半轴为-180度计算,则相位裕度应该是交点处的相角减去-180度,即单位圆交点相角加上180度。图中的所示就是相角之差,逆时针为正。
2. PM与阻尼比
PM在设计指标中更常出现是因为其与damping ratio在二阶系统中是有一定关联。从一个标准的二阶系统中,根据PM的定义,我们写成频率特性的表达式后可以精确地写出其PM的表达式。在标准二阶系统中,PM与damping ratio有如下近似关系。
常用此关系来作为系统设计的开始,但最终闭环系统的阻尼还是要再检查,因为上式仅仅适用于PM小于70,并且为标准二阶系统。

从这个关系上粗略地看,我们希望PM增大,必然会导致系统阻尼增大,从而使得系统的调节时间延长。
3.使用的局限
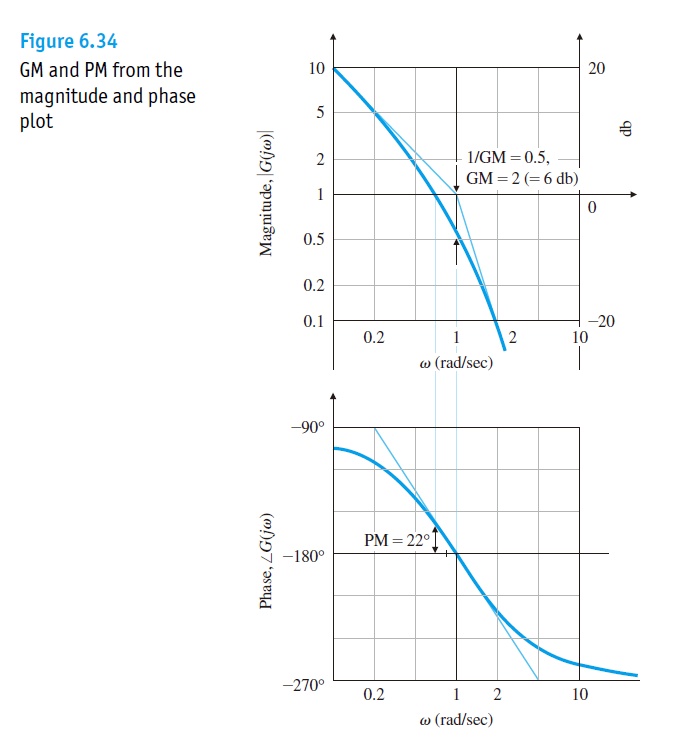
如果GM>0dB,PM>0度,则闭环系统是稳定的。此结论只适用于Nyquist Plot的半闭合曲线只与单位圆和负半实轴相交一次,且系统开环是稳定的,为最小相位系统。注意这两个条件需要一起使用才行,单独使用都不足以说明稳定性。实际中的系统一般都是采用开环Bode Plot的穿越频率(0dB处的频率)来找到对应的PM,反之GM也是 从-180度时的频率找到的。对于non-minimum phase的系统,最好还是要用Nyquist plot来确定其稳定性。
PM和GM是相对稳定性的一种表征,也必须两个一起使用才能说明问题。有可能PM为正,但GM为负或者反过来,这些都不能保证系统闭环稳定。根据[2]中所述,PM一般为30度到60度之间,GM一般大于6dB。
对于一个一阶系统或者二阶系统而言,相位永远也不会越过180度(即小于-180度),那么GM无穷大,没有参考价值。 高阶系统的Bode Plot如果与0dB线多次相交,则上述的定义并不能明确告诉我们哪一个频率下的PM是我们应该取得的。实际上在Nyquist plot中我们都会取GM为最小的值(即最靠近单位圆的交点频率),PM也为最小值,这样保守的估计对设计来讲是安全的。实际中,我们还是会采用Nyquist plot或者Nichols plot来检查GM和PM。关于Nichols plot在本系列文章中就展开了。
4.本篇小节
GM 幅值裕度和PM 相位裕度都是用来衡量闭环系统相对稳定性的。两组指标通常需要一起使用才有意义,并且两组指标的数值需要平衡系统的其他性能,因此也并不是在任何时候都是越大越好的。我们在Nyquist plot和Bode plot都能够检查GM和PM的值,但是对于其他不常规的系统,严格的GM和PM还是要通过Nyquist plot或者Nichols plot来确定。
Reference
[1] G.F. Franklin, J.D. Powell, A.Emami-Naeini, Feedback Control of Dynamic Systems, 7th Edition, 2014, Pearson
[2] 胡寿松,自动控制原理(第六版),2013,科学出版社