SVM 是是一种二分类模型，基本模型是的定义在特征空间上的间隔最大的线性分类器，SVM的学习策略就是间隔最大化。

1. 分类的边缘间隔（Margin）

1.1 分类器

以逻辑回归为例，

(

)

(

)

−

\displaystyle h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}

$h_{θ} (x) = g (θ^{T} x) = \frac{1}{1 + e ^{- θ^{T} x}}$ ，特征组合经过 sigmoid 函数被映射到

[

]

[0,1]

$[0, 1]$ 之间。
对于二分类问题，即可被视为概率，

{

(

∣

;

)

(

)

(

∣

;

)

−

(

)

\displaystyle \left\{ \begin{aligned} p(y=1|x;\theta)=h_\theta(x), \\ p(y=0|x;\theta)=1-h_\theta(x) \end{aligned} \right.

${p (y = 1 ∣ x; θ) = h_{θ} (x), p (y = 0 ∣ x; θ) = 1 - h_{θ} (x)$ 。
此时，当对样本进行分类时，则可视为

(

)

{

(

)

0.5

\displaystyle label(x)=\left\{ \begin{aligned} 1, && if\;h_\theta(x)>0.5,\\ 0, && otherwise \end{aligned} \right.

$l a b e l (x) = {1, 0, i f h_{θ} (x) > 0.5, o t h e r w i s e$

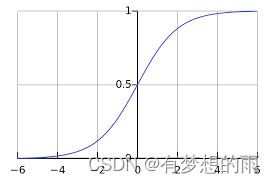
在这里插入图片描述
sigmoid 函数图像如上图所示，即当

\theta^Tx

$θ^{T} x$ 越大时，

\theta^Tx>>0

$θ^{T} x > > 0$ ，

(

)

h_\theta(x)

$h_{θ} (x)$ 越趋近于 1，则将样本

(

)

label(x)=1

$l a b e l (x) = 1$ 有更高的可信度；

同样的，当

\theta^Tx

$θ^{T} x$ 越小时，

\theta^Tx

$θ^{T} x$ <<0，

(

)

h_\theta(x)

$h_{θ} (x)$ 越趋近于 0，则将样本

(

)

label(x)=0

$l a b e l (x) = 0$ 有更高的可信度。

此时，即可视为

(

)

{

\displaystyle label(x)=\left\{ \begin{aligned} 1, && if\;\theta^Tx>>0\\ 0, && \theta^Tx<<0 \end{aligned} \right.

$l a b e l (x) = {1, 0, i f θ^{T} x > > 0 θ^{T} x < < 0$ ，可以以此作为目标函数来进行分类。

1.2 图示的边缘间隔

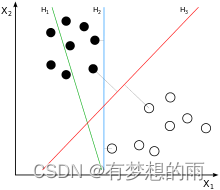
在这里插入图片描述
如上图所示，三个分类边界超平面：

H_1,H_2,H_3

$H_{1}, H_{2}, H_{3}$ ，其中，

H_1

$H_{1}$ 不能实现完全分类；

H_2

$H_{2}$ 可以，但分割面与最近的数据点只有很小的间隔，如果测试数据有一些噪声的话可能就会被

H_2

$H_{2}$ 错误分类(即对噪声敏感、泛化能力弱)，可信度不好；

H_3

$H_{3}$ 以较大间隔将它们分开，这样就能容忍测试数据的一些噪声而正确分类，是一个泛化能力不错的分类器，可信度较好。

对于线性支持向量机来说，数据点若是

$p$ 维向量，我们用

−

p-1

$p - 1$ 维的超平面来分开这些点。但是可能有许多超平面可以把数据分类。最佳超平面的一个合理选择就是以最大间隔把两个类分开的超平面。因此，SVM选择能够使离超平面最近的数据点的到超平面距离最大的超平面。

2. 函数间隔和几何间隔

2.1 分类器公式化

标签

∈

{

−

}

y\in\{-1,1\}

$y \in {- 1, 1}$ ，分类器

(

)

(

)

{

≥

−

\displaystyle h_{\omega,b}(x)=g(\omega^Tx+b)=\left\{ \begin{aligned} 1, && if\;\omega^Tx+b\ge0\\ -1, && \omega^Tx+b<0 \end{aligned} \right.

$h_{ω, b} (x) = g (ω^{T} x + b) = {1, - 1, i f ω^{T} x + b \geq 0 ω^{T} x + b < 0$

2.2 函数间隔（geometric margins ）

给定一个训练样本

(

)

(

)

(x^{(i)},y^{(i)})

$(x^{(i)}, y^{(i)})$ ，定义该样本相对于决策边界

(

)

(\omega, b)

$(ω, b)$ 的函数间隔为

(

)

(

)

(

)

\displaystyle \gamma^{(i)}=y^{(i)}(\omega^Tx^{(i)}+b)

$γ^{(i)} = y^{(i)} (ω^{T} x^{(i)} + b)$ 。

注意到，若要保证分类结果可信，需使得函数间隔

(

)

\gamma^{(i)}

$γ^{(i)}$ 是一个大的正数，因为

{

(

)

为

保

证

分

类

结

果

正

确

且

可

信

，

需

使

(

)

(

)

−

为

保

证

分

类

结

果

正

确

且

可

信

，

需

使

(

)

\displaystyle \left\{ \begin{aligned} if\;y^{(i)}=1, &&为保证分类结果正确且可信，需使\omega^Tx^{(i)}+b>0\\ if\;y^{(i)}=-1, && 为保证分类结果正确且可信，需使\omega^Tx^{(i)}+b<0 \end{aligned} \right.

${i f y^{(i)} = 1, i f y^{(i)} = - 1, 为保证分类结果正确且可信，需使 ω^{T} x^{(i)} + b > 0 为保证分类结果正确且可信，需使 ω^{T} x^{(i)} + b < 0$

因此，一个大的函数间隔代表正确且可信的分类结果。但是，注意到，如果令

;

\omega=2\omega;b=2b

$ω = 2 ω; b = 2 b$ ，此时，分类结果不变，但是函数间隔却增大了2倍，这个变化是无意义的。

给定训练集

{

(

)

(

)

;

⋯

}

S=\{(x^{(i)},y^{(i)});i=1,\cdots,n\}

$S = {(x^{(i)}, y^{(i)}); i = 1, \dots, n}$ ，将该训练集的函数间隔定义为所有训练样本中函数间隔最小的函数间隔，

即

⋯

(

)

\displaystyle \gamma=min_{i=1,\cdots,n} \gamma^{(i)}

$γ = m i n_{i = 1, \dots, n} γ^{(i)}$

2.3 几何间隔（geometric margins）

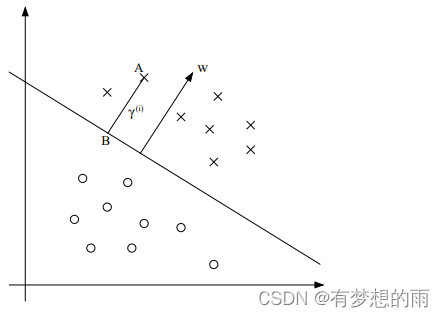
在这里插入图片描述
如上图所示，

分类面为 $(\omega, b) (ω,b)， ω \omega ω 为分类面的正交向量。$
点 A 代表标签 $y^{(i)}=1 y(i)=1 的训练样本 x ( i ) x^{(i)} x(i)，它到分类面的距离 γ ( i ) \gamma^{(i)} γ(i) 由线段 AB 给出。$
$\displaystyle \frac{\omega}{||\omega||} ∣∣ω∣∣ω 是和 ω \omega ω 同方向的单位长度向量，点 A 代表向量 x ( i ) x^{(i)} x(i) ，因此，可得点 B 为 x ( i ) − γ ( i ) ⋅ ω ∣ ∣ ω ∣ ∣ \displaystyle x^{(i)}-\gamma^{(i)}\cdot \frac{\omega}{||\omega||} x(i)−γ(i)⋅∣∣ω∣∣ω。$
点B在决策边界 $(\omega^Tx+b=0) (ωTx+b=0)上，因此有 ω T ( x ( i ) − γ ( i ) ⋅ ω ∣ ∣ ω ∣ ∣ ) + b = 0 \displaystyle \omega^T(x^{(i)}-\gamma^{(i)}\cdot \frac{\omega}{||\omega||})+b=0 ωT(x(i)−γ(i)⋅∣∣ω∣∣ω)+b=0；$
可解得， $\displaystyle \gamma^{(i)}=\frac{\omega^Tx^{(i)}+b}{||\omega||}=(\frac{\omega}{||\omega||})^Tx^{(i)}+\frac{b}{||\omega||} γ(i)=∣∣ω∣∣ωTx(i)+b=(∣∣ω∣∣ω)Tx(i)+∣∣ω∣∣b。$
定义样本 $(x^{(i)},y^{(i)}) (x(i),y(i)) 关于分类面 ( ω , b ) (\omega, b) (ω,b) 的几何间隔为 γ ( i ) = y ( i ) ⋅ [ ( ω ∣ ∣ ω ∣ ∣ ) T x ( i ) + b ∣ ∣ ω ∣ ∣ ] \displaystyle\gamma^{(i)}=y^{(i)}\cdot[(\frac{\omega}{||\omega||})^Tx^{(i)}+\frac{b}{||\omega||}] γ(i)=y(i)⋅[(∣∣ω∣∣ω)Tx(i)+∣∣ω∣∣b]。$

注意，当

∣

||\omega||=1

$∣ ∣ ω ∣ ∣ = 1$ 时，几何间隔和函数间隔相同。而 几何间隔具有参数的尺度缩放不变性。如，令

;

\omega=2\omega;b=2b

$ω = 2 ω; b = 2 b$ ，几何间隔仍不变。

给定训练集

{

(

)

(

)

;

⋯

}

S=\{(x^{(i)},y^{(i)});i=1,\cdots,n\}

$S = {(x^{(i)}, y^{(i)}); i = 1, \dots, n}$ ，将该训练集的几何间隔定义为所有训练样本中几何间隔最小的几何间隔，

即

⋯

(

)

\displaystyle \gamma=min_{i=1,\cdots,n} \gamma^{(i)}

$γ = m i n_{i = 1, \dots, n} γ^{(i)}$

3. 最优间隔分类器——硬间隔（optimal margin classifier）

为使分类器的结果是正确的，且具有可信度，不仅需要使得分类面可以将正负样本分开，且需使得正负训练样本之间有一定的间隙，即几何间隔。

3.1 数学描述

假定训练集是线性可分的，存在一个可以将正负样本分开的分类面的超平面集合，要从该集合中找到最优分类面，即最大化 几何间隔。可以将其视为优化问题，即

(

)

(

)

≥

⋯

∣

max_{\gamma,\omega,b}\;\gamma\\ st.\;y^{(i)}(\omega^Tx^{(i)}+b)\ge\gamma,i=1,\cdots,n\\ ||\omega||=1

$m a x_{γ, ω, b} γ s t . y^{(i)} (ω^{T} x^{(i)} + b) \geq γ, i = 1, \dots, n ∣ ∣ ω ∣ ∣ = 1$
即最大化

\gamma

$γ$ ，使得训练集中每个样本的函数间隔至少是

\gamma

$γ$ ，

∣

||\omega||=1

$∣ ∣ ω ∣ ∣ = 1$ 确保函数间隔等于几何间隔，
即保证了所有的几何间隔大于等于

\gamma

$γ$ 。

3.2 求解

3.2.1 问题转化

上述问题是一个优化问题，但是其约束条件

∣

||\omega||=1

$∣ ∣ ω ∣ ∣ = 1$ 是非凸问题，不能使用标准的解决凸优化的问题求解。将其转换为：

max

⁡

∣

(

)

(

)

≥

⋯

\displaystyle\max_{\hat\gamma,\omega,b}\;\frac{\hat\gamma}{||\omega||}\\ st.\;y^{(i)}(\omega^Tx^{(i)}+b)\ge\hat\gamma,i=1,\cdots,n

$\overset{γ}{^}, ω, b max \frac{γ ^}{∣ ∣ ω ∣ ∣} s t . y^{(i)} (ω^{T} x^{(i)} + b) \geq \overset{γ}{^}, i = 1, \dots, n$
即转换为最大化

∣

\frac{\hat\gamma}{||\omega||}

$\frac{γ ^}{∣ ∣ ω ∣ ∣}$ ，几何间隔和函数间隔通过

∣

\gamma=\frac{\hat\gamma}{||\omega||}

$γ = \frac{γ ^}{∣ ∣ ω ∣ ∣}$ 联系起来。但是，目标函数

∣

\frac{\gamma}{||\omega||}

$\frac{γ}{∣ ∣ ω ∣ ∣}$ 依然是非凸函数。

注意到，对

\omega,b

$ω, b$ 参数的尺度缩放不影响最终结果。因此，若对

\omega,b

$ω, b$ 进行尺度缩放，使得他们对应的训练集的函数间隔

\hat\gamma=1

$\overset{γ}{^} = 1$ 。

此时，目标函数则变为最大化

∣

\frac{\hat\gamma}{||\omega||}=\frac{1}{||\omega||}

$\frac{γ ^}{∣ ∣ ω ∣ ∣} = \frac{1}{∣ ∣ ω ∣ ∣}$ ，这相当于最小化

∣

||\omega||^2

$∣ ∣ ω ∣ ∣^{2}$ ，此时，优化问题变为：

min

⁡

∣

(

)

(

)

≥

⋯

\displaystyle\min_{\omega,b}\;\frac{1}{2}||\omega||^2\\ st.\;y^{(i)}(\omega^Tx^{(i)}+b)\ge1,i=1,\cdots,n

$ω, b min \frac{1}{2} ∣ ∣ ω ∣ ∣^{2} s t . y^{(i)} (ω^{T} x^{(i)} + b) \geq 1, i = 1, \dots, n$
此时，该问题变为一个凸二次目标函数，同时约束只有线性约束。它的解就是 最优间隔分类器。

3.2.2 拉格朗日对偶求解方法（The optimal margin classifier）

3.2.2.1 原问题与对偶问题

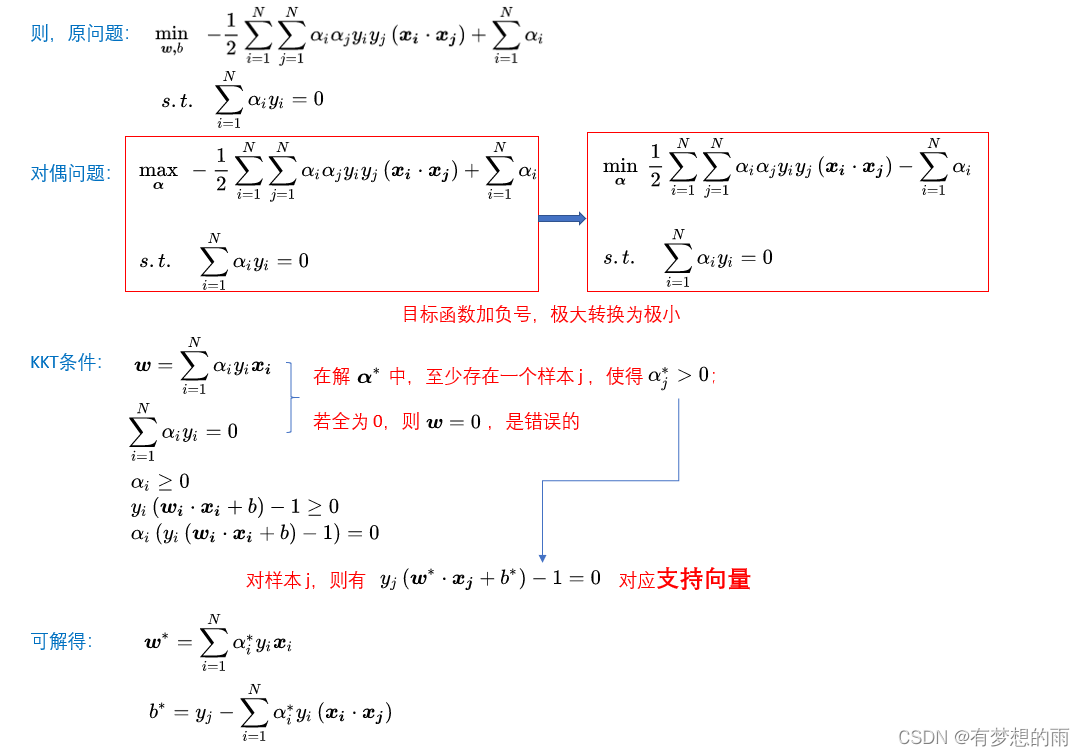
在这里插入图片描述

3.2.2.2 KKT条件

在这里插入图片描述

3.2.3 求解

为利用拉格朗日方法求解，这里将原问题转化为：

min

⁡

∣

(

)

−

(

)

(

)

≤

⋯

\displaystyle\min_{\omega,b}\;\frac{1}{2}||\omega||^2\\ \\ st.\;g_i(\omega)=-y^{(i)}(\omega^Tx^{(i)}+b)+1\le0,\;i=1,\cdots,n

$ω, b min \frac{1}{2} ∣ ∣ ω ∣ ∣^{2} s t . g_{i} (ω) = - y^{(i)} (ω^{T} x^{(i)} + b) + 1 \leq 0, i = 1, \dots, n$

而KKT的互补松弛条件，即当训练集中有样本点的函数间隔明确等于 1 时（此时对应着

(

)

g_i(\omega)=0

$g_{i} (ω) = 0$ ）。如下图所示，最大分隔边界的超平面如实线所示。间隔最小的点事距离决策面最近的点。此处有三个点（两个正样本，一个负样本），虚线穿过这三个点与决策面平行。

\alpha_i

$α_{i}$ 分别对应着这三个训练样本点。这三个样本点就是 支持向量。
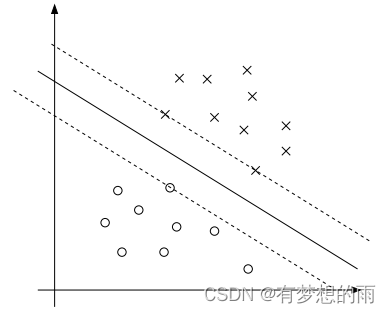
在这里插入图片描述
实际问题中支持向量的个数远小于训练集的样本数。在决定最佳分类面时只有支持向量起作用，而其他数据点并不起作用。

在这里插入图片描述

原文链接：https://blog.csdn.net/qq_41536160/article/details/125513766

1. 分类的边缘间隔（Margin）

1.1 分类器

1.2 图示的边缘间隔

2. 函数间隔和几何间隔

2.1 分类器公式化

2.2 函数间隔（geometric margins ）

2.3 几何间隔（geometric margins）

3. 最优间隔分类器——硬间隔（optimal margin classifier）

3.1 数学描述

3.2 求解

3.2.1 问题转化

3.2.2 拉格朗日对偶求解方法（The optimal margin classifier）

3.2.2.1 原问题与对偶问题

3.2.2.2 KKT条件

3.2.3 求解

你可能也喜欢