3、实验二矩阵连乘

实验内容

n个矩阵连乘，不满足交换律，但是满足结合律，通过不同的加括号方式，会使得需要的乘法次数不同。用动态规划方法计算，找出最优加括号方式，使总的乘法次数最少。

解题思路

将矩阵连乘积Ai Ai +1 … Aj简记为A[i:j]，这里i≤j。
考察计算A[i:j]的最优计算次序。设这个计算次序在矩阵Ak和Ak+1之间将矩阵链断开，i≤k<j，则其相应完全加括号方式为（Ai Ai +1…Ak）（Ak+1 Ak+2… Aj）。
计算量：A[i:k]的计算量加上A[k+1:j]的计算量，再加上A[i:k]和A[k+1:j]相乘的计算量。

源代码

package b矩阵连乘;

public class MatrixText {
	public static void main(String agrs[]) {
		int[] p = { 30, 35, 15, 5, 10, 20, 25 };
//		int[] p = { 30,15,5,20,3 };
		int n = p.length;
		System.out.print("您输入的矩阵为：");
		for (int i = 0; i < n - 1; i++) {
			System.out.print("A" + (i + 1) + "[" + p[i] + "]" + "[" + p[i + 1] + "]" + "  ");
		}
		System.out.println("\n");
		int[][] m = new int[n][n];
		int[][] s = new int[n][n];
		Utils.matrixChain(p, m, s);
		// 打印m矩阵
		System.out.println("The m["+(n-1)+"]["+(n-1)+"] 矩阵：");
		for (int i = 1; i < m.length; i++) {
			for (int j = 1; j < m.length; j++) {
				if (i > j) {
					System.out.print("0" + "\t");
				} else {
					System.out.print(m[i][j] + "\t");
				}
			}
			System.out.println();
		}
		System.out.println();
		// 打印s矩阵
		System.out.println("The s["+(n-1)+"]["+(n-1)+"] 矩阵：");
		for (int i = 1; i < s.length; i++) {
			for (int j = 1; j < s.length; j++) {
				if (i > j) {
					System.out.print("0" + "\t");
				} else {
					System.out.print(s[i][j] + "\t");
				}
			}
			System.out.println();
		}
		System.out.println();
		System.out.println("矩阵连乘加括号方式为：");
		Utils.OptimalParens(s, 1, n - 1);

	}

}

package b矩阵连乘;

public class Utils {

	/**
	 * @see 计算最优值
	 * @param p：各个矩阵的下标
	 * @param m：最优解矩阵
	 * @param s：最优解矩阵所取得k值的矩阵
	 */
	public static void matrixChain(int[] p, int[][] m, int[][] s) {
		int n = p.length - 1;// 求出矩阵的个数
		// 给m矩阵主对角线赋值为0
		for (int i = 1; i <= n; i++) {
			m[i][i] = 0;
		}
		for (int r = 2; r <= n; r++)
			for (int i = 1; i <= n - r + 1; i++) {
				int j = i + r - 1;
				// 给矩阵设置一个超大值，为后面的比较做准备
				m[i][j] = 999999999;
				for (int k = i; k < j; k++) {
					// 计算相乘的次数
					int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
					if (t < m[i][j]) {
						// 给m和s矩阵赋值
						m[i][j] = t;
						s[i][j] = k;
					}
				}
			}
	}

	/**
	 * @see 打印加括号的最优解方案
	 * @param s：最优解矩阵所取得k值的矩阵
	 * @param i：矩阵的第一个A1
	 * @param j：矩阵的最后一个A(n-1)
	 */
	public static void OptimalParens(int[][] s, int i, int j) {
		if (i == j) {
			System.out.print("A" + i);
		} else if (i + 1 == j) {
			System.out.print(" (A" + i + " A" + j + ") ");
		} else {
			System.out.print(" (");
			// 递归调用
			OptimalParens(s, i, s[i][j]);
			OptimalParens(s, s[i][j] + 1, j);
			System.out.print(") ");
		}
	}

}

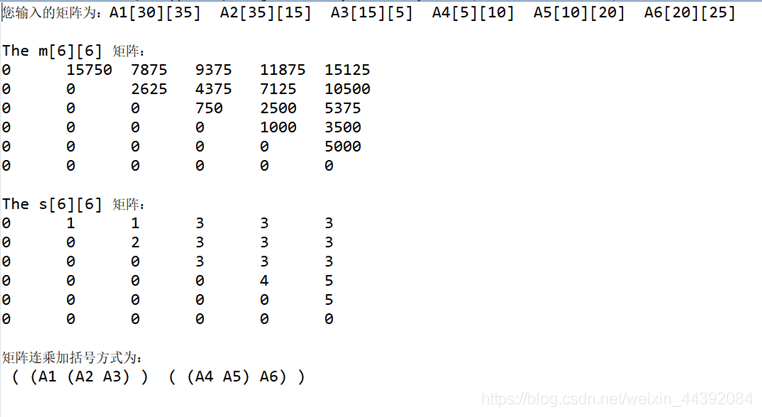
运行截图