一、树

1、概念

下面就是一颗很常见的树：

2、实现

function Tree(value) {
  this.value = value;
  this.children = [];
}
const A = new Tree("A");
const B = new Tree("B");
const C = new Tree("C");
const D = new Tree("D");
A.children.push(B, C, D);

树的模型如下：

这里树里面我们研究的重点是二叉树。

二、二叉树

1、概念

二叉树有很多性质：

1. 二叉树是每个节点最多有两个子树的树结构(度为2)。子树称作“左子树”（left subtree）和“右子树”（right subtree）
2. 在二叉树的第i层上至多有2^(i-1)个结点（i>0），
3. 深度为k的二叉树至多有2^k-1个结点（k>0）,满二叉树即为2^k-1个节点
4. 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1
5. 具有n个结点的完全二叉树的深度必为 log2(n+1)
6. 对*[完全二叉树]，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

2、遍历

对下面的二叉树进行遍历

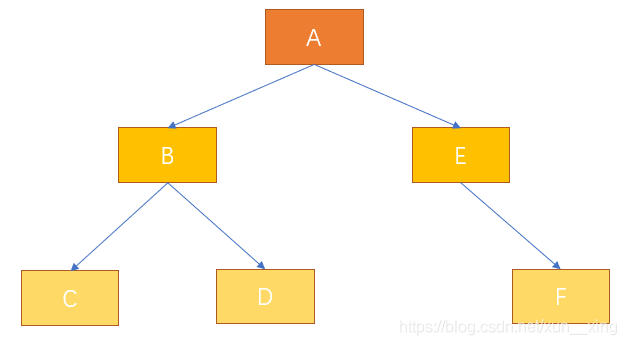
前序遍历：ABCDEF
中序遍历：CBDAEF
后序遍历：CDBFEA
注意点：
1）已知 前序遍历序列 和 中序遍历序列，可以唯一确定一颗二叉树
2）已知 中序遍历序列和 后序遍历序列，可以唯一确定一颗二叉树

3、遍历实现

1.树的实现

function Tree(value) {
  this.value = value;
  this.left = null;
  this.right = null;
}
const A = new Tree("A");
const B = new Tree("B");
const C = new Tree("C");
const D = new Tree("D");
const E = new Tree("E");
const F = new Tree("F");
A.left = B;
B.left = C;
B.right = D;
A.right = E;
E.right = F;

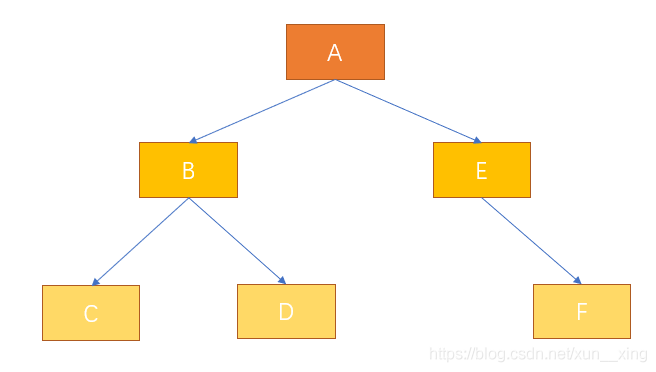
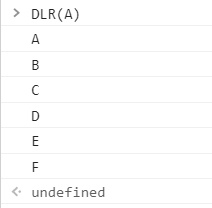
2.前序遍历

function DLR(root){
  if(!root){
    return;
  }
  // 输出自己
  console.log(root.value);
  // 输出左边
  DLR(root.left);
  // 输出右边
  DLR(root.right);
}

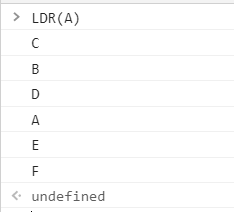
3.中序遍历

function LDR(root){
  if(!root){
    return;
  }
  // 输出左边
  LDR(root.left);
  // 输出自己
  console.log(root.value);
  // 输出右边
  LDR(root.right);
}

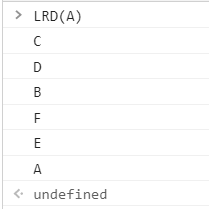
4.后序遍历

function LRD(root){
  if(!root){
    return;
  }
  // 输出左边
  LRD(root.left);
  // 输出右边
  LRD(root.right);
  // 输出自己
  console.log(root.value);
}

3、前序、中序确定二叉树

function getTree(dlr, ldr) {
    if (dlr.length !== ldr.length) {
        throw new Error("无解");
    }
    if (dlr.length === 0) {
        return null;
    }
    var newvalue = dlr[0];//找到根
    var root = new Node(newvalue);//创建根节点
    //左边
    var index = ldr.indexOf(newvalue);//根节点在中序遍历中的索引
    var leftldr = ldr.slice(0, index);//左边的中序遍历结果
    var leftdlr = dlr.slice(1, 1 + leftldr.length);//左边的前序遍历结果
    root.left = getTree(leftdlr, leftldr);
    //右边
    var rightldr = ldr.slice(index + 1);//右边的中序遍历结果
    var rightdlr = dlr.slice(1 + leftldr.length);//右边的前序遍历结果
    root.right = getTree(rightdlr, rightldr);
    return root;
}

4、二叉树的深度

function getDeep(root){
  if(!root){
    return 0;
  }
  return 1+Math.max(getDeep(root.left),getDeep(root.right));
}

5、查询二叉树

function deepSearch(root, value) {
    if (!root) {
        return false;
    }
    if (root.value === value) {
        return true;
    }
    return searchTree(root.left, value) || searchTree(root.right, value);
}
console.log(searchTree(res, "B"));

博主开始运营自己的公众号啦，感兴趣的可以关注“飞羽逐星”微信公众号哦，拿起手机就能阅读感兴趣的文章啦！