文章目录

一、为什么要讲动态规划呢？
二、什么是动态规划
三、感受一下递归算法、备忘录算法、动态规划
四、动态规划的解题套路

我建议直接看下面的参考文章，因为大佬的讲解非常到位，我这里做的笔记肯定是没那么详细的，这里只是给我自己做个记录

看一遍就理解：动态规划详解
 算法-动态规划 Dynamic Programming–从菜鸟到老鸟

一、为什么要讲动态规划呢？

我们刷leetcode的时候，经常会遇到动态规划类型题目。动态规划问题非常非常经典，也很有技巧性，一般大厂都非常喜欢问。学就要学一些回报最大的知识

二、什么是动态规划

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

以上定义来自维基百科，看定义感觉还是有点抽象。简单来说，动态规划其实就是，给定一个问题，我们把它拆成一个个子问题，直到子问题可以直接解决。然后呢，把子问题答案保存起来，以减少重复计算。再根据子问题答案反推，得出原问题解的一种方法。

相信看到这里，我们可以知道动态规划也用到HashMap集合，如果还不会，请看我另一篇博客，让你秒懂Java集合框架

动态规划核心思想
动态规划最核心的思想，就在于拆分子问题，记住过往，减少重复计算。然而我认为记不记住过往不重要，重要的是不要重复计算子问题就行了。例如自顶向下就需要备忘录，自底向上就不需要备忘录了。
在这里插入图片描述
我们来看下，网上比较流行的一个例子

A ： “1+1+1+1+1+1+1+1 =？”
A ： “上面等式的值是多少”
B ：计算 “8”
A : 在上面等式的左边写上 “1+” 呢？
A : “此时等式的值为多少”
B : 很快得出答案 “9”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”

三、感受一下递归算法、备忘录算法、动态规划

leetcode原题：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。

有些小伙伴第一次见这个题的时候，可能会有点蒙圈，不知道怎么解决。其实可以试想：

要想跳到第10级台阶，要么是先跳到第9级，然后再跳1级台阶上去;要么是先跳到第8级，然后一次迈2级台阶上去。
同理，要想跳到第9级台阶，要么是先跳到第8级，然后再跳1级台阶上去;要么是先跳到第7级，然后一次迈2级台阶上去。
要想跳到第8级台阶，要么是先跳到第7级，然后再跳1级台阶上去;要么是先跳到第6级，然后一次迈2级台阶上去。

假设跳到第n级台阶的跳数我们定义为f(n)，很显然就可以得出以下公式：

f（10） = f（9）+f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
…
f(3) = f(2) + f(1)
即通用公式为: f(n) = f(n-1) + f(n-2)

我们现在确定一下界限

通常设为为0和1，但是0代表还没有上阶梯，所以要从1开始。再根据公式f(n) = f(n-1) + f(n-2)，可以知道界限需要设为1，2，并且f(1) = 1，f(2) = 2.

递归算法

class Solution {
    public int numWays(int n) {
    if(n == 1){
        return 1;
    }
     if(n == 2){
        return 2;
    }
    return numWays(n-1) + numWays(n-2);
    }
}

去leetcode提交一下，发现有问题，超出时间限制了
在这里插入图片描述
为什么超时了呢？递归耗时在哪里呢？先画出递归树看看：

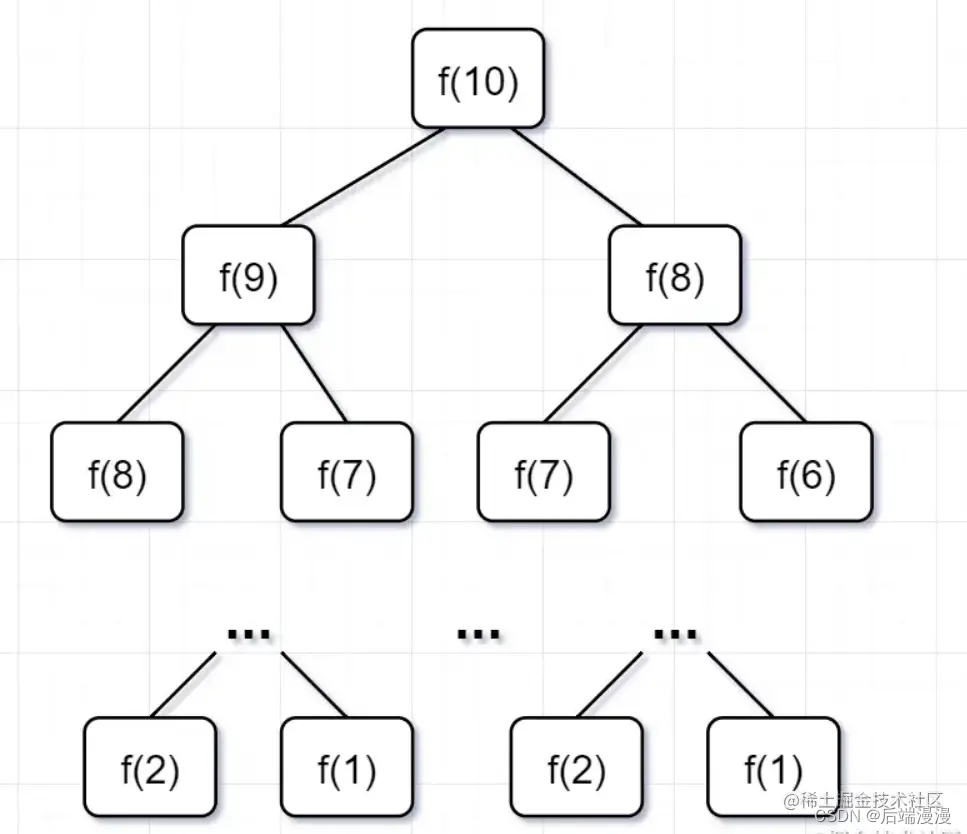
我们先来看看这个递归的时间复杂度吧：

递归时间复杂度 = 解决一个子问题时间*子问题个数

一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以复杂度是 O(1)；
问题个数 = 递归树节点的总数，递归树的总节点 = 2^{n-1，所以是复杂度O(2}n)。

因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n)，就是指数级别的，爆炸增长的，如果n比较大的话，超时很正常的了。

既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去备忘录查一下，如果有，就直接取就好了，备忘录没有才开始计算，那就可以省去重新重复计算的耗时啦！这就是带备忘录的解法。

带备忘录的递归解法（自定向下）

一般使用一个数组或者一个哈希map充当这个备忘录。

第一步，f（10）= f(9) + f(8)，f(9) 和f（8）都需要计算出来，然后再加到备忘录中，如下：
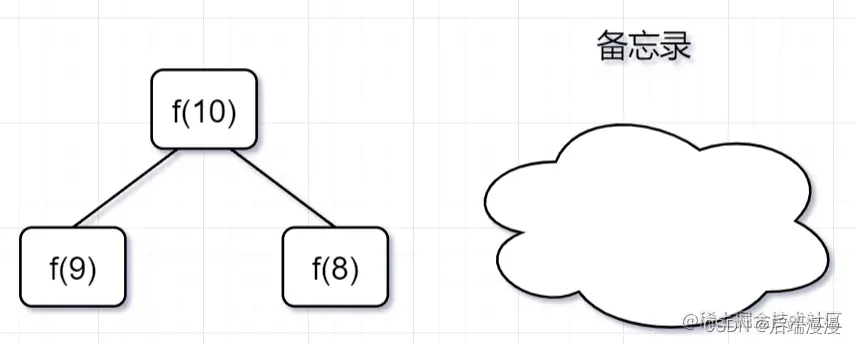
在这里插入图片描述
第二步， f(9) = f（8）+ f（7），f（8）= f（7）+ f(6), 因为 f(8) 已经在备忘录中啦，所以可以省掉，f(7),f（6）都需要计算出来，加到备忘录中~

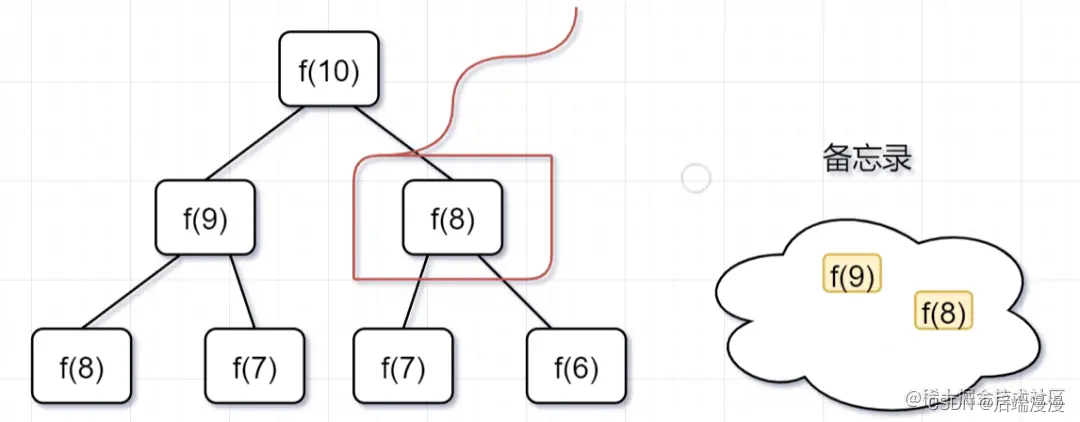
第三步， f(8) = f（7）+ f(6),发现f(8)，f(7),f（6）全部都在备忘录上了，所以都可以剪掉。
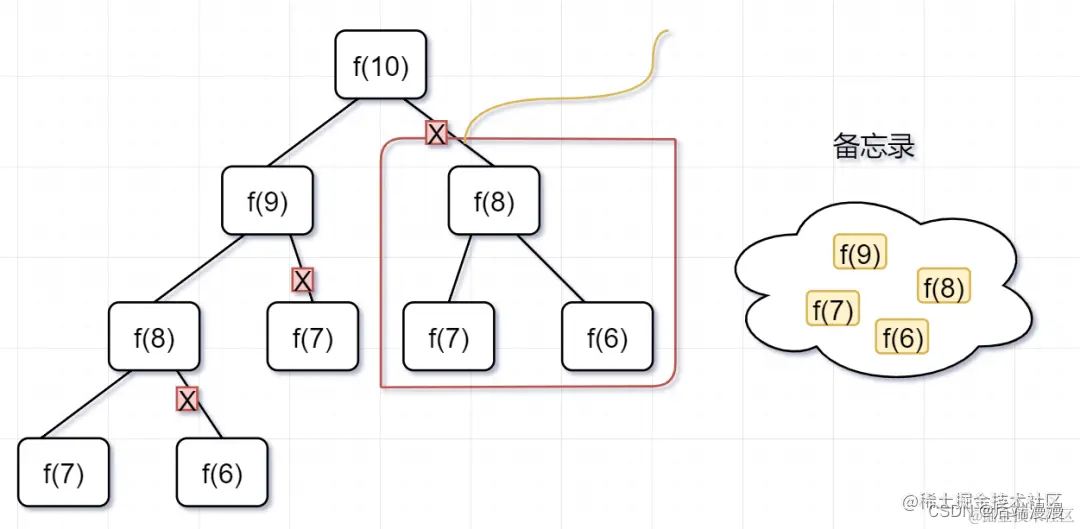
在这里插入图片描述
所以呢，用了备忘录递归算法，递归树变成光秃秃的树干咯，如下：

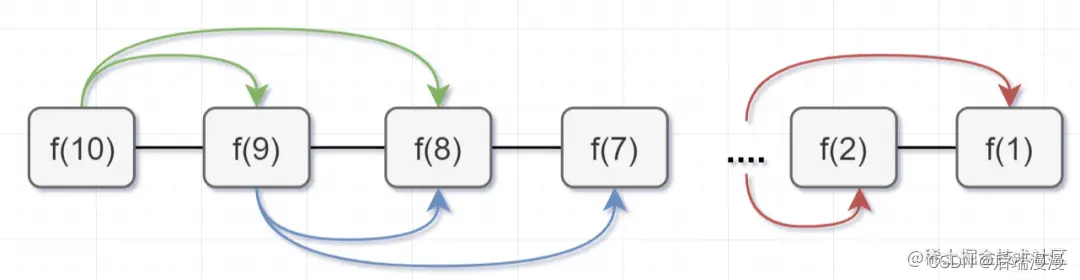
带备忘录的递归算法，子问题个数=树节点数=n，解决一个子问题还是O(1),所以带备忘录的递归算法的时间复杂度是O(n)。接下来呢，我们用带备忘录的递归算法去撸代码，解决这个青蛙跳阶问题的超时问题咯~，代码如下：

public class Solution {
    //使用哈希map，充当备忘录的作用
    Map<Integer, Integer> tempMap = new HashMap();
    public int numWays(int n) {
        // n = 0 也算1种
        if (n == 0) {
            return 1;
        }
        if (n <= 2) {
            return n;
        }
        //先判断有没计算过，即看看备忘录有没有
        if (tempMap.containsKey(n)) {
            //备忘录有，即计算过，直接返回
            return tempMap.get(n);
        } else {
            // 备忘录没有，即没有计算过，执行递归计算,并且把结果保存到备忘录map中，对1000000007取余（这个是leetcode题目规定的）
            tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);
            return tempMap.get(n);
        }
    }
}

自底向上的动态规划

动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也都是差不多。但是呢：

带备忘录的递归，是从f(10)往f(1）方向延伸求解的，所以也称为自顶向下的解法。
动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10）方向，往上推求解，所以称为自底向上的解法。

动态规划有几个典型特征，最优子结构、状态转移方程、边界、重叠子问题,在青蛙跳阶问题中：

f(n-1)和f(n-2) 称为 f(n) 的最优子结构

f(n)= f（n-1）+f（n-2）就称为状态转移方程

f(1) = 1, f(2) = 2 就是边界啦

比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。

public class Solution {
    public int numWays(int n) {
        if (n<= 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }
        int a = 1;
        int b = 2;
        int temp = 0;
        for (int i = 3; i <= n; i++) {
            temp = (a + b)% 1000000007;
            a = b;
            b = temp;
        }
        return temp;
    }
    }

四、动态规划的解题套路

什么样的问题可以考虑使用动态规划解决呢？

如果一个问题，可以把所有可能的答案穷举出来，并且穷举出来后，发现存在重叠子问题，就可以考虑使用动态规划。

比如一些求最值的场景，如最长递增子序列、最小编辑距离、背包问题、凑零钱问题等等，都是动态规划的经典应用场景。

动态规划的解题思路：

穷举分析，即做树状图找规律

确定边界

去欸的那个最优子结构

写出状态转移方程

1. 穷举分析

当台阶数是1的时候，有一种跳法，f（1） =1
当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2;
当台阶是3级时，想跳到第3级台阶，要么是先跳到第2级，然后再跳1级台阶上去，要么是先跳到第 1级，然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) =3
当台阶是4级时，想跳到第3级台阶，要么是先跳到第3级，然后再跳1级台阶上去，要么是先跳到第 2级，然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) =5
当台阶是5级时…

2. 确定边界

通过穷举分析，我们发现，当台阶数是1的时候或者2的时候，可以明确知道青蛙跳法。f（1） =1，f(2) = 2，当台阶n>=3时，已经呈现出规律f(3) = f(2) + f(1) =3，因此f（1） =1，f(2) = 2就是青蛙跳阶的边界。

3. 确定最优子结构

n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构？有这么一个解释：

4. 写出状态转移方程

通过前面3步，穷举分析，确定边界，最优子结构，我们就可以得出状态转移方程啦

原文链接：https://blog.csdn.net/m0_46638350/article/details/129013111