定义
这三种表达式做题都会用到

导数定义的第二种表达形式

导数定义的第三种表达形式

导数的四种符号
做题中都会遇到,所以都要掌握

常见函数的导数
都要掌握
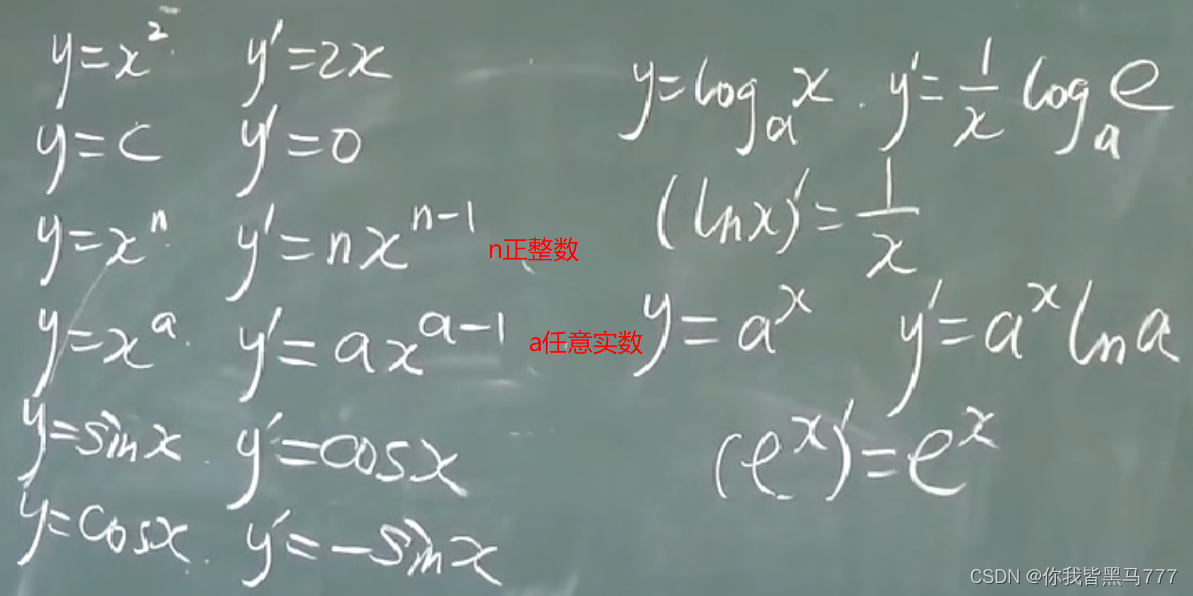
题型
例1: 用导数的定义求一个函数的导数
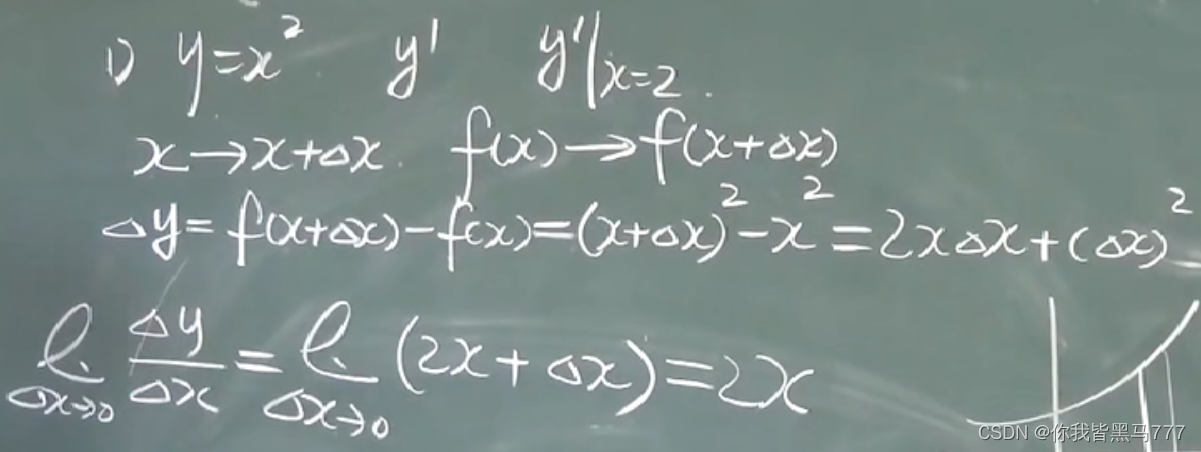
导数意义 
左右导数的定义

结论: 在一点处可导它的充要条件是左右导数存在且相等
总结: 如果考察到在某点上可导的讨论的话,一般都是用这个结论,先把左导数求出来,再把右导数求出来,看看是否相等
题型: 考查在某点上可导性
例1 
这种题难点在求极限的时候要用到两个重要极限或洛必达法则,肯定有技巧
可导与连续的关系
定理 : 可导必连续
可导必连续的定义
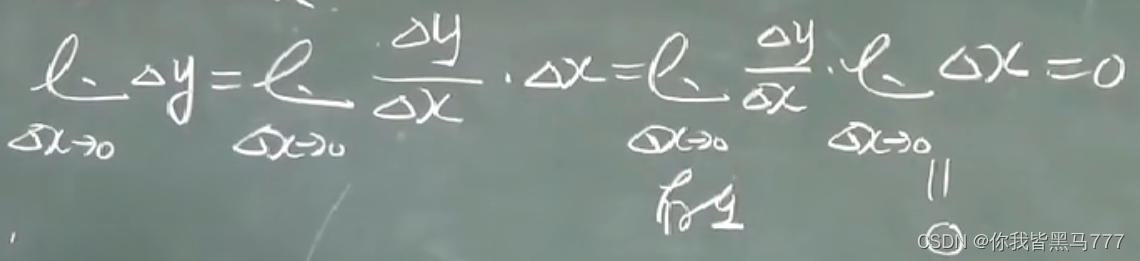

得出结论: 可导必连续,但连续不一定可导
思考:为什么连续不一定可导?老师说可导的几何意义必须是光滑的,但连续可以是一条直线,所以直线方程是不可导的
例题


版权声明:本文为m0_57832432原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。