博客

顺序存储定义

线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。

顺序存储方式

      线性表的顺序存储结构，就是在内存中找了块地儿，通过站位的形式，把一定内存空间给占了，然后把相同数据类型的数据元素依次存放到这块空地中【可通过C中的一维数组来实现顺序存储结构】。

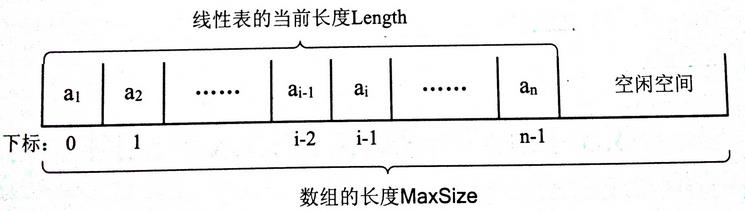
描述顺序存储结构需要三个属性：
1. 存储空间的起始位置：数组 data , 它的存储位置就是存储空间的存储位置
2. 线性表的最大存储容量
3. 线性表的当前长度

数组长度 与 线性表长度区别
– 数组长度：
即存放线性表的存储空间的长度，存储分配后这个量一般是不变的。

• 线性表长度：
  即线性表中数据元素的个数

在任意时刻，线性表的长度应该小于等于数组的长度。

地址计算方法

      线性表是从1开始的，而数组的下标是从0开始的，因此 线性表的第 i 个元素是要存储在数组下标为 i - 1 的位置，即数据元素的序号和存放它的数组下标之间存在对应关系。

存储器中的每个存储单元都有自己的编号，这个编号称为地址。

• 假设每个数据元素占用的是 c 个 存储单元，那么线性表中第 i + 1 个数据元素的存储位置和第 i 个数据元素的存储位置满足关系 ： LOC ( ai+1 ) = LOC ( ai ) + c ;
• 第 i 个数据元素 ai 的存储位置： LOC ( ai ) = LOC ( a1 ) + （i – 1） c*

由上式公式得出结论：

1. 通过上面公式可随时算出线性表中任意位置的地址，不管它是第一个还是最后一个，都是相同的时间。
2. 那么对每个线性表位置的存取数据，对于计算机来说都是相等时间，即是一个常数，即存取时间性能为 O(1).

3. 把具有以上特点的存储结构称为随机存储结构

   顺序存储结构的插入与删除

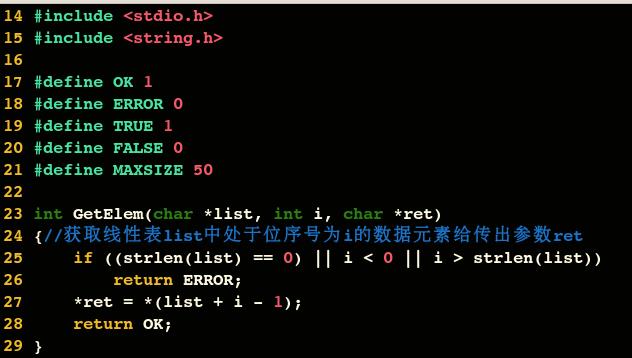
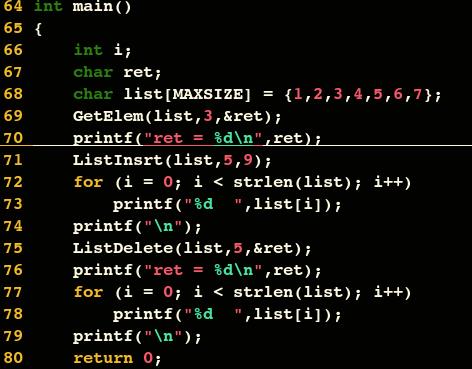
获得元素操作

 对于线性表的顺序存储结构来说，要实现获得元素操作，即将线性表 L 中的第 i 个位置元素值返回。

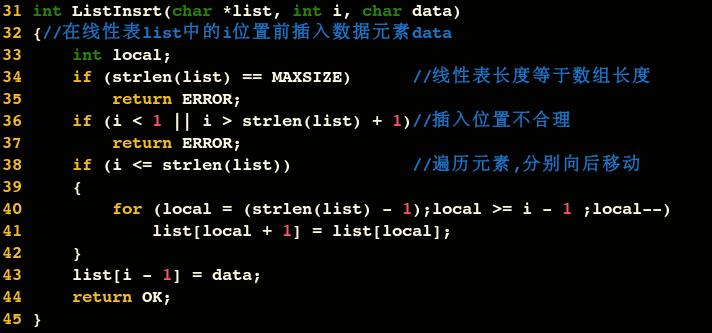
插入操作

插入算法的思路：

1. 如果插入位置不合理，抛出异常
2. 如果线性表长度大于等于数组长度，则抛出异常或动态增加容量
3. 从最后一个元素开始向前遍历到第 i 个位置，分别将它们都向后移动一个位置
4. 将要插入元素填入位置 i 处
5. 表长加1

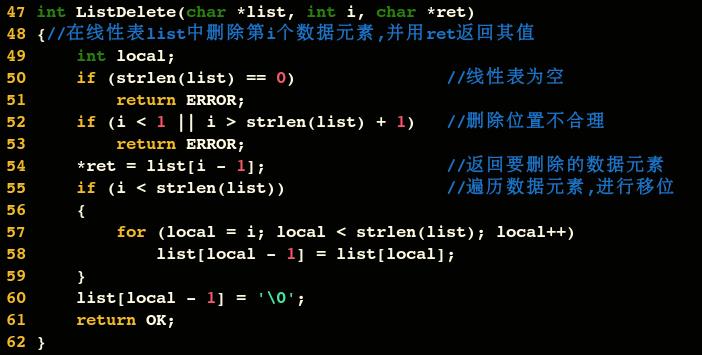
删除操作

删除算法的思路：

1. 如果删除位置不合理，抛出异常
2. 取出删除元素
3. 从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置
4. 表长减1

分析插入和删除的时间复杂度：

最好的情况：插入或删除的都是最后一个元素，时间复杂度 O（1）
最坏的情况：插入或删除的都是第一个元素，则所有其他元素都要进行移动，时间复杂度 O(n)
平均的情况：插入或删除第 i 个元素，需要移动 n – i 个元素，时间复杂度 O(n)

结论：
线性表的顺序存储结构，在存、取数据时，不管是哪个位置，时间复杂度都是O(1)，而插入和删除时，时间复杂度都是 O(n)。
适合元素个数不太变化，而更多是存储数据的应用。