计算机语言运用–数值计算9-方程的计算机处理91-5_Matlab
计算机:电子线路组成的计算机器。人与计算机则是通过计算机语言-符号系统说给计算机听而交流。
计算机语言有低级语言-机器语言、汇编、高级语言-C/C++/C#/VB/PASCAL/LISP/JAVA/PYTHON/……成百上千种之多。
作为一种计算机器—可以协助人类处理各种事情—数值计算问题、文字处理问题、图形图像处理问题、事务问题……。自从有了数字计算的计算机器,几乎所有的可以交给计算机的事情,都交给计算机来处理—是辅助处理—按照人们的要求—事先安排的模式进行处理。
数值计算
方程的计算机处理
这里说的方程,是以实数域为计算范围。
这里说的方程:是含有未知数的等式。
可以是a+5=8,或X+A=B,或ax2+bx+c=0,或ax+by=c与dx-ey=f,或ax"+bx=c,或,或
……、……
计算机如何处理这些问题呢?,问题的描述是什么样子的,才能充分利用计算机呢?
当然是代数形式的。便于计算机发挥特长,便于程序软件的重用性。通过用户交互,决定将什么样的具体问题交给计算机进行数值处理。
方程的计算机处理:
MATLAB语言及其平台
从最简单的起步,再逐级复杂,以便体会程序编写、方程的手工预处理及其人机交互。
可以用脚本文件—解释型、动态数据类型的计算机语言连续自动运行模式
a=input(‘输入第一个数 ‘)
b=input(‘输入第二个数 ‘)
x=b-a;
disp(‘输出计算结果 x=b-a=’),x
disp(‘输出计算结果 x=b+a=’),b+a
disp(‘输出计算结果x=b*a=’),b*a
disp(‘输出计算结果x=b/a=’),b/a
感觉咋样?什么是方程的计算机处理—算法及其描述,运行及其人机交互。
从最简单的代数方程计算机处理开始,通过计算机语言的运行了解、理解程序编写需要的格式。算法描述的计算机处理模式–将方程进行必要的改变,适合计算机语言描述,适合计算机按照数字电路的逻辑模式进行处理。
X+a=b型的方程需要进行改造,成为—-X=b-a的样式;
计算机是进行数值计算的好帮手,因此需要对a,b预先赋值,再进行计算;
那么对于三元一次方程组呢?也是如此。当然,最好是用求解方程的三个解的公式来进行处理—也就是,用它们作为计算机语言描述的基础。当然,需要计算机语言描述判别分母的问题。这样,便有了方程处理的前期工作,手工处理。

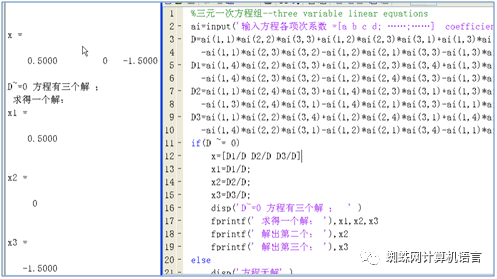
%三元一次方程组–threevariable linear equations
ai=input(‘输入方程各项次系数 =[a b cd; ……;……] coefficient = ‘);
D=ai(1,1)*ai(2,2)*ai(3,3)+ai(1,2)*ai(2,3)*ai(3,1)+ai(1,3)*ai(2,1)*ai(3,2)…
-ai(1,1)*ai(2,3)*ai(3,2)-ai(1,2)*ai(2,1)*ai(3,3)-ai(1,3)*ai(2,2)*ai(3,1)
D1=ai(1,4)*ai(2,2)*ai(3,3)+ai(1,2)*ai(2,3)*ai(3,4)+ai(1,3)*ai(3,2)*ai(2,4)…
-ai(1,4)*ai(2,3)*ai(3,2)-ai(1,2)*ai(2,4)*ai(3,3)-ai(1,3)*ai(2,2)*ai(3,4)
D2=ai(1,1)*ai(2,4)*ai(3,3)+ai(1,4)*ai(2,3)*ai(3,1)+ai(1,3)*ai(3,4)*ai(2,1)…
-ai(1,3)*ai(2,4)*ai(3,1)-ai(1,4)*ai(2,1)*ai(3,3)-ai(1,1)*ai(3,4)*ai(2,3)
D3=ai(1,1)*ai(2,2)*ai(3,4)+ai(1,2)*ai(2,4)*ai(3,1)+ai(1,4)*ai(3,2)*ai(2,1)…
-ai(1,4)*ai(2,2)*ai(3,1)-ai(1,2)*ai(2,1)*ai(3,4)-ai(1,1)*ai(3,2)*ai(2,4)
if(D ~= 0)
x=[D1/D D2/DD3/D]
x1=D1/D;
x2=D2/D;
x3=D3/D;
disp(‘D~=0 方程有三个解; ‘ ),x1,x2,x3
fprintf(‘ 求得一个解: ‘),x1
fprintf(‘ 解出第二个: ‘),x2
fprintf(‘ 解出第三个: ‘),x3
else
disp(‘方程无解’ )
end
运行结果
MATLAB函数验证
a=[1 2 3 ;-56 -7;9 -10 11]
b=[-4 8 -12]’
x=a\b
看看运行结果
>> a= [1 2 3 ;-5 6 -7;9 -10 11]
b= [-4 8 -12]’
x=a\b
a =
1 2 3
-5 6 -7
9 -10 11
b =
-4
8
-12
x =
0.5000
0.0000
-1.5000
>>
这就是MATLAB的优势。它将常用的数学问题求解,都做成了库函数,用户简单调用即可。
咱不是要说明实际数学问题怎么变成计算机处理吗!就是数学方程的预先处理问题、计算机语言描述问题嘛。
在C、C++、C#、Fortran等语言中,你就能看到这个问题的处理与描述。