比如下图,虽然它们的重合度不高,但是它们的结构是一样的,应当认为它们是很相似的,请问如何量化的判断呢?有什么好的算法?

做过一个小研究是关于判断曲线的相似性的,下面正文答案已经基本上解决了该问题。使用归一化后的Fréchet distance即可。另外也可使用Hausdorff distance,但是使用效果不如前者。
推荐几篇论文仅供参考:Alt H, Godau M (1995) Computing the Fréchet distance between two polygonal curves International Journal of Computational Geometry & Applications 5:75-91. doi:10.1142/S0218195995000064
Fréchet MM (1906) Sur quelques points du calcul fonctionnel Rendiconti del Circolo Matematico di Palermo (1884-1940) 22:1-72. doi:10.1007/BF03018603
此外,可以使用离散化的方法使用Fréchet distance,以便于实际编程计算,同推荐一篇离散化的文章供参考,里面有该方法的伪代码,另matlab也有现成的package,搜搜即可。
Eiter T, Mannila H (1994) Computing discrete Fréchet distance See Also
最后推荐一个应用该方法的实例,为了解决Fréchet distance中阈值的问题对其进行了标准化从而得到一个相似指数。
Wang J, Xu C, Tong S, Chen H, Yang W (2013) Spatial dynamic patterns of hand-foot-mouth disease in the People’s Republic of China Geospatial health 7:381-390
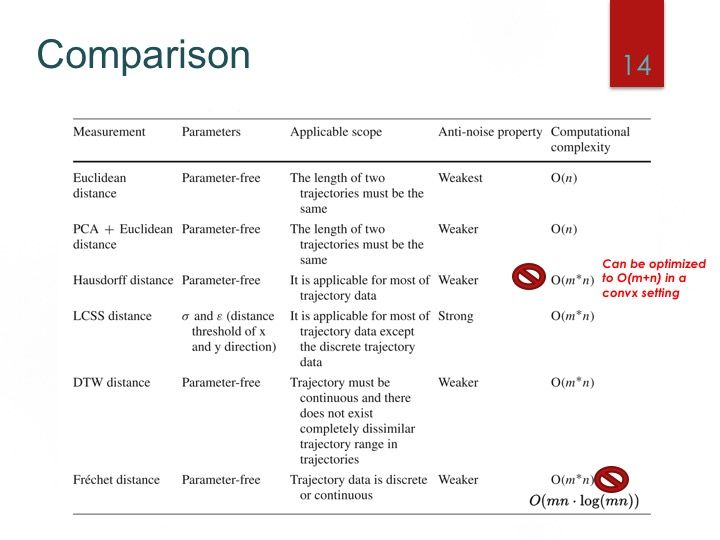
判断两条轨迹的相似性方法有很多
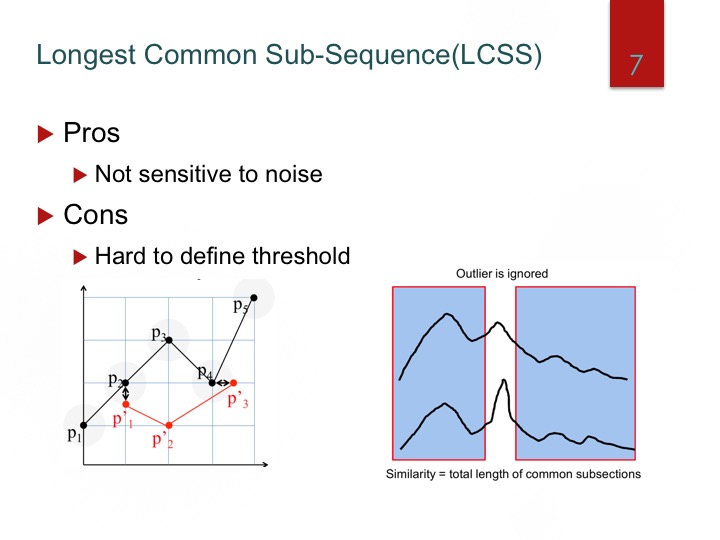
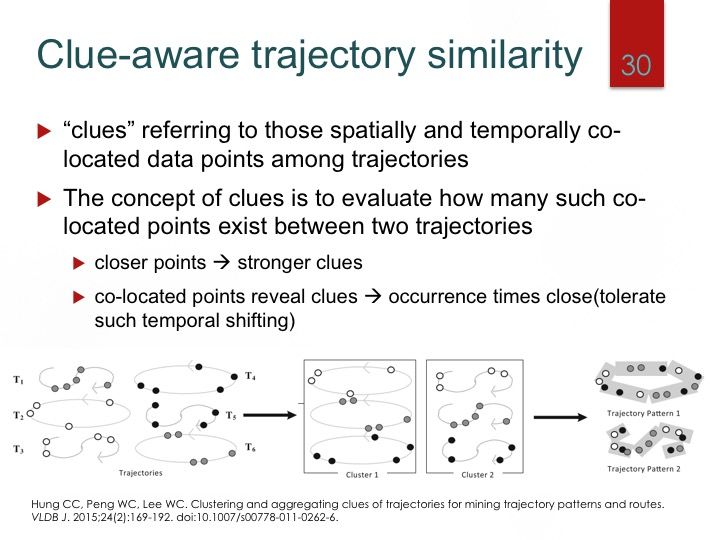
基于点方法: EDR,LCSS,DTW等
基于形状的方法: Frechet, Hausdorff(该方法可以解决上述问题)
基于分段的方法:One Way Distance, LIP distance
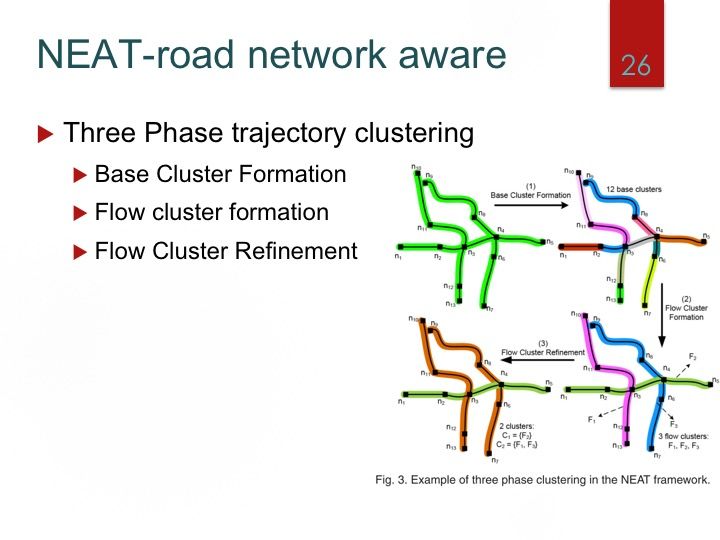
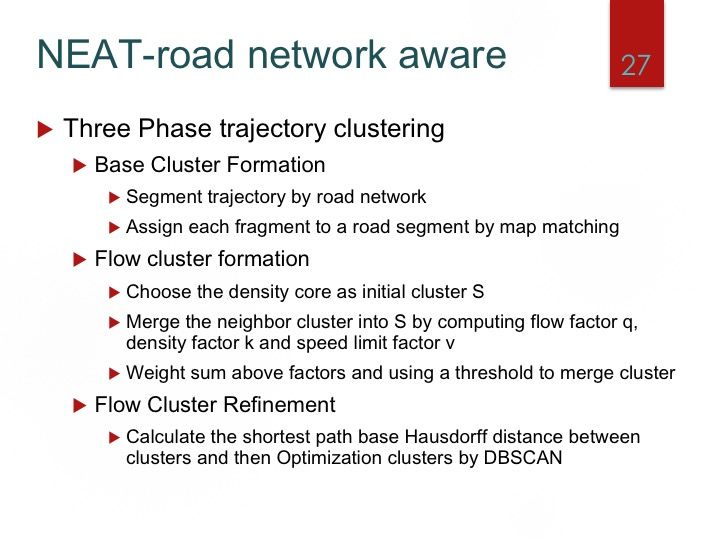
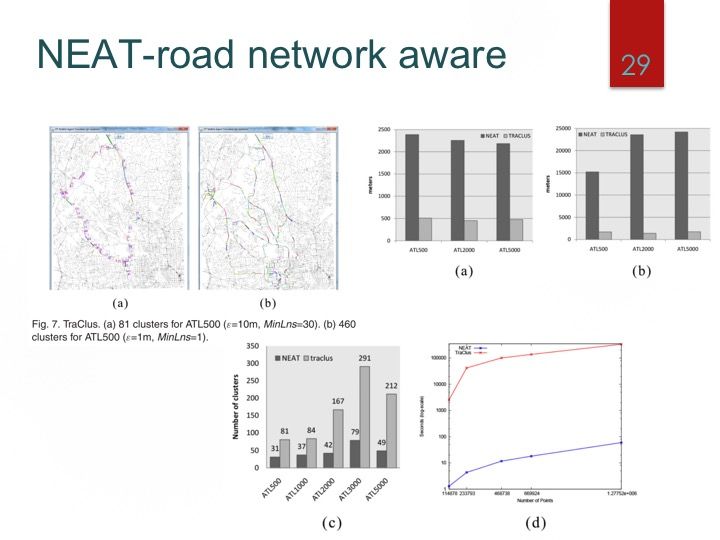
基于特定任务的方法:TRACLUS, Road Network,grid等
附上本人总结的Trajectory Distance slides:

























作者:Di Yao
链接:https://www.zhihu.com/question/27213170/answer/271567963
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。