引言
灰色理论
灰色模型介于白色模型与黑色模型之间,其是内部信息部分确知、部分信息不确知的系统。因此,灰色系统理论主要研究的就是“外延明确,内涵不明确”的“小样本,贫信息”问题。
灰色模型(GM模型)
如果一个系统具有层次、结构关系的模糊性,动态变化的随机性,指标数据的不完备或不确定性,则称这些特性为灰色性。具有灰色性的系统称为灰色系统。主要分元素信息不完全, 结构信息不完全, 边界信息不完全, 运行行为信息不完全四种情况。
对灰色系统建立的预测模型称为灰色模型(GreyModel),简称GM模型,它揭示了系统内部事物连续发展变化的过程。灰色模型通过少量的、不完全的信息,建立灰色微分预测模型,对事物发展规律作出模糊性的长期描述(模糊预测领域中理论、方法较为完善的预测学分支)。
其优点:(1)所需信息量较少,即不需要大量样本(一般有4个以上数据即可建模);(2)不需要知道原始数据分布的先验特征,即样本不需要有规律性分布,通过有限次的生成,可将无规则分布(或服从任意分布)的任意光滑离散的原始序列转化为有序序列; (3)计算工作量小;(4)可保持原系统特征,定量分析结果与定性分析结果不会不一致, 能较好地反映系统实际情况, 预测准确度高。因此,适用于大规模定制生产的质量预测分析。
灰色模型在极小样本量情况下进行质量数据预测具有独特的优势,预测效果也相对较好.
基于灰色模型的大规模定制生产质量预测
大规模定制生产过程质量控制与大批量生产过程比较具有以下新的特点:
(1)样本量较小,尤其是在定制化程度较高的情况下和生产的初级阶段;
(2)样本数列往往具有时变性,不能简单假设其服从正态分布;
(3)大规模定制生产模式要求灵活性和快速性,而传统的质量控制方法响应速度偏慢。
灰色模型GM(1,1)是灰色系统理论中较常用的预测模型, 基于该模型的质量指标预测建模步骤如下:
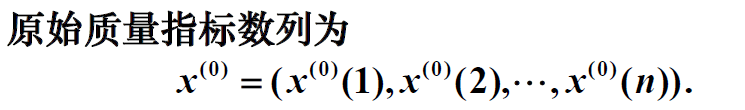
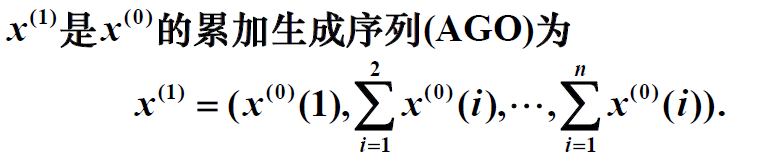
经过该处理, 可使粗糙的原始离散数列变为光滑的离散数列【GM(1,1)建模条件要求数据具有准光滑性】。
生成AGO序列的Matlab命令:x1=cumsum(x0)
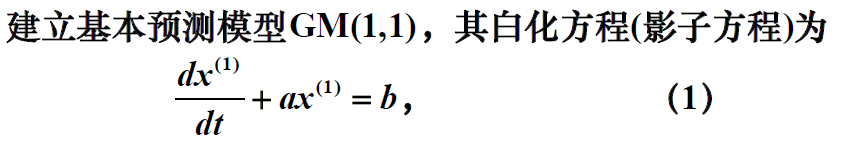
上式中a称为发展灰度, b称为内生成控制灰度, 且符合
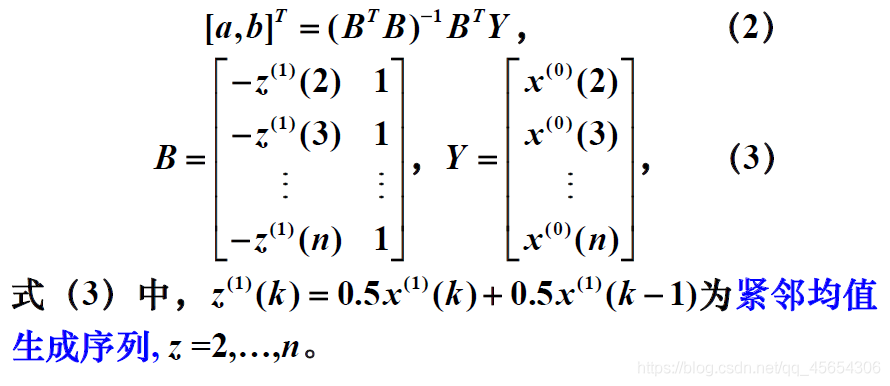
之所以用z(k),是为了进一步取平均,从而光滑化。
对建立的GM(1,1)预测模型进行精度检验和评估,检验依据后验差比值c和小误差概率p两个指标,模型精度等级见表1。其中c和p定义如下:

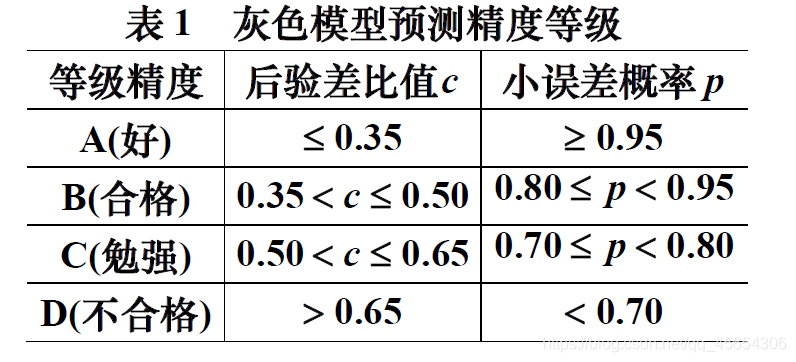
对于指标值对应模型精确性, c越小越好, p越大越好。

若要进一步提高预测精度,可采用GM(1,1)新陈代谢模型:
(1) 采用原始序列建立一个GM(1,1)模型,按上述方法求出一个预测值;
(2) 将该预测值补入已知数列中,同时去除一个最旧的数据;
(3) 在(2)基础上再建立GM(1,1)模型,求出下一个预测值。
以此类推,通过预测灰数的新陈代谢,逐个预测,
依次递补,可以得到之后几期的数据,对原始数据数量进行有效扩充。