打算每天复习一点算法内容,就先从动态规划下手。曾经动态规划让我头疼,重新学了一下觉得还好啦不是很难,实现动态规划算法的核心在于实现它的递推公式,写出递推公式,代码也就很容易了。
动态规划类似分治法,都是将一个大问题分解为一个个小问题,分而治之。不同之处在于,动态规划记忆了重复的子问题,避免了运算过程中的重复计算。
适用情况:有重叠子问题和最优子结构性质(动态规划每一步求的都是最优解)的问题。
下面我们通过经典的动态规划问题(0-1背包问题)来学习这个算法。
问题描述:将N件物品选几件放入容量为W(重量)的背包中,每件物品有自己的重量w和价值v,要求在不超过背包容量情况下使背包内放入的物品总价值最高。
分析:①不超过背包容量,有:Σw[i]<=W (i表示第i件物品)
②对于“将前i件物品放入容量为j的背包中”这个子问题,现只考虑第i件物品放还是不放,如果放了的话,问题转换为“前i-1件物品放入剩下j-w[i]容量的背包中”,如果不放,问题转换为“前i-1件物品放入容量为j的背包中”。这两种情况的优者为当前问题的最优解。
③根据②的分析,得到如下递推公式

其中,0<=i<=N,0<=j<=W.
④例子
5个物品的重量和价值分别为(5,12),(4,3),(7,10),(2,3),(6,6),背包容量15
初始化表

根据公式填表
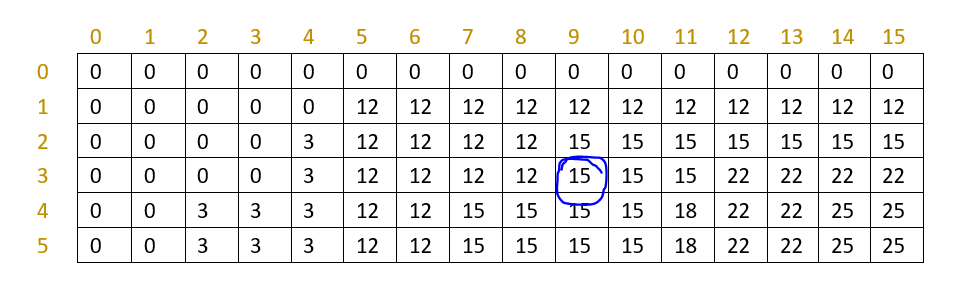
随便选一个来分析,比如上表圈中位置f[3][9]表示前3件物品放入容量为9的背包中,最高价值为15
15如何来的呢?
考虑第三件物品放还是不放入背包,若放入背包f[3][9]=f[2][9-w[3]]+v[3]=f[2][2]+v[3]=0+10=10
若不放入背包,f[3][9]=f[2][9]=15
因为15>10,所有第三件物品不放入背包,前3件物品放入容量为9的背包得到的最高价值是15
⑤代码——代码中有两种方法列举具体方案
#include<iostream>
#include<time.h>
#include<map>
using namespace std;
int main()
{
//(5,12),(4,3),(7,10),(2,3),(6,6)背包容量15
int f[6][16] = {0};
int application[6][16];
int weight[5] = {5,4,7,2,6 };
int value[5] = {12,3,10,3,6};
clock_t start, end;
int n = 10000;
start = clock();
while (n--)
{
for (int i = 1;i < 6;i++)
{
for (int j = 1;j < 16;j++)
{
if (j - weight[i - 1] >= 0)
{
if (f[i - 1][j] > f[i - 1][(j - weight[i - 1])] + value[i - 1])
{
f[i][j] = f[i - 1][j];//不放
application[i][j] = 0;
}
else
{
f[i][j] = f[i - 1][(j - weight[i - 1])] + value[i - 1];
application[i][j ] = 1;
}
//f[i][j] = f[i - 1][j] > f[i - 1][(j - weight[i - 1])] + value[i - 1] ? f[i - 1][j] : f[i - 1][(j - weight[i - 1])] + value[i - 1];
}
else
{
f[i][j] = f[i - 1][j];//不放
application[i][j] = 0;
}
}
}
}
end = clock();
cout << "运行时间为:"<<(end-start)*1.0/10000<< endl;
cout << "动态规划表:" << endl;
for (int i = 0;i < 6;i++)
{
for (int j = 0;j < 16;j++)
{
cout << f[i][j]<<" ";
}
cout << endl;
}
cout << "放入背包的物品有:" << endl;
int j = 15;
//第一种得到具体方案的方法:
for (int i = 5;i > 0;i--)
{
if (f[i][j] != f[i - 1][j])
{
cout<<"物品" << i << "加入背包" << endl;
j = j - weight[i-1];
}
}
//第二种得到具体方案的方法
j = 15;
for (int i = 5;i > 0;i--)
{
if (application[i][j])//放了
{
cout << "物品" << i << "加入背包" << endl;
j = j - weight[i - 1];
}
}
return 0;
}我们也可以不使用application存储具体情况,通过倒推的方式计算出背包价值最大化情况下存放的物品。以下通过javascript实现:
function dynamic (W, N, weight, value) {
let f = []
for (let i = 0; i <= N; i++) {
if (!f[i]) f[i] = []
for (let j = 0; j <= W; j++) {
if (i === 0 || j === 0) {
f[i][j] = 0
continue
}
if (j - weight[i - 1] >= 0) {
let notIn = f[i-1][j]
let canIn = f[i-1][j - weight[i - 1]] + value[i - 1]
f[i][j] = notIn > canIn ? notIn : canIn
} else {
f[i][j] = f[i-1][j]
}
}
}
let i = N
let j = W
while (i > 0) {
if (f[i][j] !== f[i-1][j]) {
console.log(`放入了第${i}个物品`, weight[i-1], value[i-1])
j = j - weight[i - 1]
}
i--
}
return f[N][W]
}
let weight = [5,4,7,2,6] // 5个物品的重量
let value = [12,3,10,3,6] // 5个物品的价值
let W = 15 // 背包容量
let N = weight.length
console.log(dynamic(W, N, weight, value))空间复杂度优化
从上面的代码我们可以看出,f是一张N*W的二维数组表,事实上我们每算一个f[i][j]所依赖的只有f[i-1][j] 和 f[i-1][j-weight[i-1]]两个值,即第i行只依赖上一行便能计算出结果,我们可以考虑只存储两行数据。
function dynamic (W, N, weight, value) {
let prev = new Array(W + 1).fill(0)
let current = new Array(W + 1).fill(0)
for (let i = 0; i <= N; i++) {
for (let j = 0; j <= W; j++) {
if (j - weight[i - 1] >= 0) {
let notIn = prev[j]
let canIn = prev[j - weight[i - 1]] + value[i - 1]
current[j] = notIn > canIn ? notIn : canIn
} else {
current[j] = prev[j]
}
}
prev = current
current = []
}
return prev[W]
}
let weight = [5,4,7,2,6] // 5个物品的重量
let value = [12,3,10,3,6] // 5个物品的价值
let W = 15 // 背包容量
let N = weight.length
console.log(dynamic(W, N, weight, value))