一、特殊矩阵的使用
(1) zeros函数:产生全0矩阵,即零矩阵
(2)ones函数:产生全1局者,即幺矩阵
(3)eye函数:产生对角线为1的矩阵。当矩阵是方阵时,得到一个单位阵。
(4)rand函数:产生(0,1)区间均匀分布的随机矩阵
(5)randn函数:产生均值为0,方差为1的标准正态分布随机矩阵
举例:


分析:
% rand函数:产生(0,1)开区间均匀分布的随机数x
% fix(a+(b-a+1)*x):产生[a,b]区间上均匀分布的随机整数
% randn函数:产生均值为0、方差为1的标准正态分布随机数x
% u+ ax: 得到均值为u, 方差为a^2的随机数
>>A = fix(10+(99-10+1)*rand(5))
>>B = 0.6+sqrt(0.1)*randn(5)
>>C = eye(5)
>>(A+B)*C == C*A +B*C
ans = 1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
二、用于专门学科的特殊矩阵
(1)魔法矩阵

% 魔方矩阵 由1,2,3…n^2个整数组成,且每行每列以及主、副对角线各n元素之和都相等
% M = magic(8);
% disp(M);
% disp(sum(M(1,:)));
% disp(sum(M(:,1)));
>> study_6
64 2 3 61 60 6 7 57
9 55 54 12 13 51 50 16
17 47 46 20 21 43 42 24
40 26 27 37 36 30 31 33
32 34 35 29 28 38 39 25
41 23 22 44 45 19 18 48
49 15 14 52 53 11 10 56
8 58 59 5 4 62 63 1
260
260
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
5 -10 10 -5 1
-10 30 -35 19 -4
10 -35 46 -27 6
-5 19 -27 17 -4
1 -4 6 -4 1
>>
(2)范德蒙矩阵:用于通讯系统的纠错编码中,如图所示。
% M = vander(1:5);
% disp(M);

(3)希尔伯特矩阵 行号+列号的倒数,
% format rat
% H = hilb(4);
% disp(H);

(4)伴随矩阵 compan(P) p是一个多项式的系数向量

(5) 帕斯卡矩阵P = pascal

三、矩阵的变换
(1)对角阵:提取矩阵对角线的元素
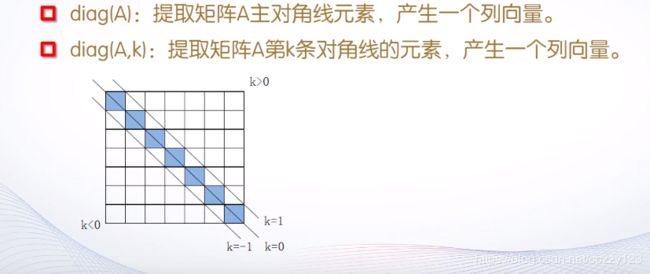
% 提取矩阵对角线元素
% A = fix(10+(99-10+1)*rand(5));
% disp(A);
% B = diag(1:5);
% disp(B);
% C = B*A;
% disp(C);
% A = fix(10+(99-10+1)*rand(5));
% disp(A);
% B = diag(1:5);
% C = A*B;
% disp(C);
(2)三角阵:上三角阵和下三角阵:%上三角阵 triu(A),triu(A,k);
(3)矩阵的转置 :小数点后加单引号
%上三角阵 triu(A),triu(A,k);
%矩阵旋转rot90(A,k)
%矩阵的转置 小数点后面接单引号 单引号(共轭转置)
%矩阵的翻转 fliplr(A) 矩阵左右翻转
%flipud 上下翻转
例题:验证魔方阵的主对角线、对角线元素之和相等

(4)逆矩阵:inv(A)
例题:

四、矩阵求值
(1)矩阵的行列式值:
%行列式求值 det(A)
(2)矩阵的秩:线性无关的行数或者列数
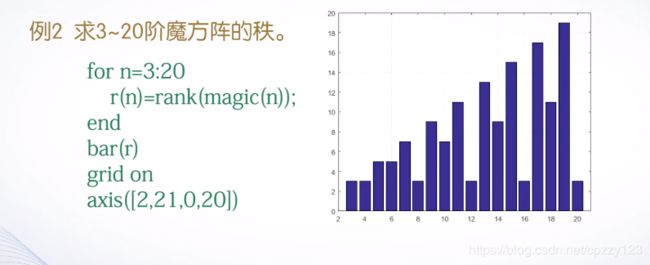
规律:

(3)矩阵的迹:对角线元素和或者特征值和

(4)矩阵的范数:
%向量的矩阵和范数
%1范数,向量元素的绝对值之和
%2范数,向量元素平方和的平方根
%无穷范数:向量元素绝对值中的最大值 norm
norm(V)、norm(V,1)计算向量V的一范数
norm(V,inf);
%1范数,矩阵列元素绝对值之和的最大值
%2范数,矩阵最大特征值的平方根
%无穷范数:矩阵行元素绝对值之和的最大值
(5)矩阵的条件数:描述矩阵的性能(%矩阵条件数:A的范数 与A逆矩阵的范数乘积 越接近1 矩阵性能越好)

五、矩阵的特征值和特征向量
(1)矩阵特征值的数学定义:


例题:


结论:

(2)特征值的几何意义:
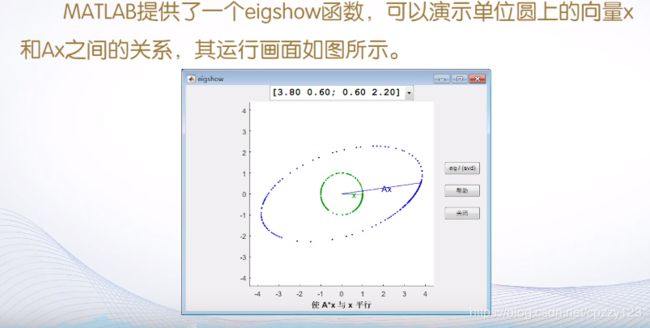
六、稀疏矩阵
(1)定义:0元素个数多于非0个数
(2) 矩阵的存储方式:

(3)存储方式:

(4)存储方式的转化:

(5)直接建立稀疏存储矩阵:Sparse、spconvert

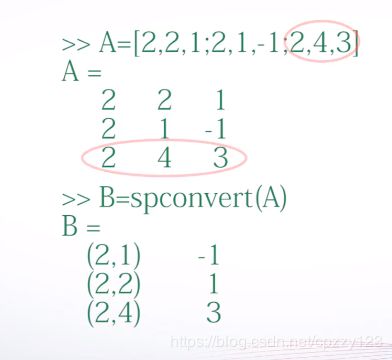
(6)带状稀疏矩阵:非零元素在对角线上 ,speye产生单位稀疏矩阵


总结:
第二篇介绍了Matlab矩阵的运算处理