博客

汉明距离(Hamming distance)是计算两个向量之间不同对应元素数量之和。本文介绍R、Python语言的计算过程。

汉明距离概述

汉明距离是以美国数学家理查德·汉明的名字命名的，他在1950年关于汉明码的论文中提出了该举例度量指标。它被广泛用于多个学科，如信息论、编码理论和密码学。

举例：
“karolin” 和 “kathrin” 两个字符串汉明距离为s 3 (差异字符有: r-t, o-h, l-r),

1011100 和 1001000 汉明距离为 2 (不同二进制数为: 1-0 和 1-0)

31738 和 32337 汉明距离为 3 (不同整数位: 1-2, 7-3, 和 8-7).

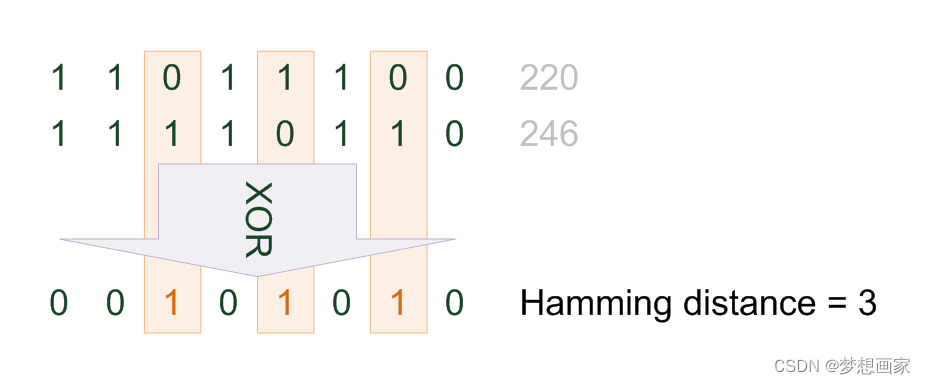
汉明距离在解决很多问题中被证明是非常有用。例如，在编码理论中它被用于错误检测和纠错码；在遗传学中它被用来衡量基因差异；在机器学习算法中用来寻找相似点或区别。

实现函数

假设有两个向量 x = [1, 2, 3, 4] ；y = [1, 2, 5, 7] .
它们之间的汉明距离为2，因为最后两个对应元素不同。

R语言的计算逻辑为：

sum(x != y)

Python的计算过程为：

# 自定义函数实现
def hammingDistance(s1, s2):
    """返回等长序列之间的汉明距离"""
    if len(s1) != len(s2):
        raise ValueError("Undefined for sequences of unequal length")
    return sum(el1 != el2 for el1, el2 in zip(s1, s2))

当然也可以使用 scipy.spatial.distance 包 hamming 函数直接计算。

示例1(二值类型)

下面示例计算两个包括二值向量之间的距离：

# R语言实现
# 创建向量
x <- c(0, 0, 1, 1, 1)
y <- c(0, 1, 1, 1, 0)
sum(x != y)

# [1] 2

Python代码实现：

from scipy.spatial.distance import hamming

x = [0, 1, 1, 1, 0, 1]
y = [0, 0, 1, 1, 0, 0]

hamming(x, y) * len(x)

# 2.0

示例2(数值类型)

数值类型向量的汉明距离：

# 创建向量
x <- c(7, 12, 14, 19, 22)
y <- c(7, 12, 16, 26, 27)

# 计算汉明距离
sum(x != y)

# [1] 3

Python代码实现：

from scipy.spatial.distance import hamming

x = [7, 12, 14, 19, 22]
y = [7, 12, 16, 26, 27]

hamming(x, y) * len(x)

# 3.0

示例3(字符串类型)

计算字符串类型汉明距离：

# 创建向量
x <- c('a', 'b', 'c', 'd')
y <- c('a', 'b', 'c', 'r')

# 计算汉明距离
sum(x != y)

# [1] 1

Python语言实现：

from scipy.spatial.distance import hamming 

# 定义数组
x = ['a', 'b', 'c', 'd']
y = ['a', 'b', 'c', 'r']

hamming(x, y) * len(x)

# 1.0

总结

本文介绍了汉明距离，并通过示例介绍R和Python语言的实现过程。