博客

参考：https://www.cnblogs.com/SunArmy/p/9837348.html

位运算符

• ±*/是给十进制位来进行计算的，&|~^是给二进制来进行计算的。

• 位运算符分为逻辑运算符和移位运算符

• 二进制中0代表false，1代表true

逻辑运算符

• 逻辑运算符分为 与（&）、或（|）、非（~）、异或（^）四种

  • 与(&)：同true(1)/false(0)为true(1)/false(0)
    • 例如：4&7=4
      
  • 或(|)： 遇true(1)即true(1)
    • 例如：4|7=7
      
  • 非(~)： 也就是取反
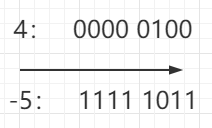
    • 例如~4=-5
      
  • 异或(^)：同true或同false为false(0)，一true(1)一false(0)才为true(1)
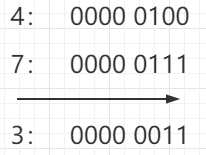
    • 例如：4^7=3
      

  注意：十进制中我们用±来表示正负，在二进制，我们用最高位来表示正负，如果是1的表示这个二进制对应十进制是个负数，相反，是正数。 也就是说，二进制的最高位就是符号位。

  整数取反快速口诀：
  正数取反，正数加一，再取负；例如：~4=-5
  负数取反，负数加一，再取正；例如：~-4=3

移位运算符

• 移位运算符分为 左移位<<、右移位>> 和 无符号右移位>>>
  • 左移位<<：所有位上的数字向左移动，尾部不够就补0
    • 例如：8<<2=2
      
  • 右移位>>：所有位上的数字向右移动，头部不够的时候看最高位，最高位是0就补0，是1就补1。
    • 例如：8>>2= 32
      
  • 无符号右移位>>>：所有位上的数字向右移动，头尾部不够都补0，且只对32位和64位有效（其实这句话不是很明白？32位和64位？？）

  注意：移位运算的快速计算方法：
  左移位：m * 2的n次方
  右移位：m / 2的n次方

二进制相关

• 几进制，就是每一位上最多能表示几个数。例如，十进制，就是每一位上可以表示 0~9十个数字；二进制，就是每一位上可以表示 0~ 1两个数字；八进制每一位可以表示0~7 八个数字。

二进制与十进制的相互转换

• 二进制转十进制
  • 正数：二进制的每一位从右往左分别乘以2的下标次方
    • 例如：00000111=1* 2^0+ 1*2^1 + 1 * 2^2=7 (注意：这里的^ 代表次方，不是上面逻辑运算符中的异或)
  • 负数：需用到补码，原码减一后取反，对应十进制数在取负就行
    • 例如：1111 1010
      
• 十进制转二进制
  • 正数：正数只需要除以2，记录余数，并将每次的商继续除以2直到商0。
    • 例如：12的二进制为：0000 1100
      
  • 负数：负数的二进制就要用到补码，先计算负数的绝对值的原码，再取反，最后加1
    • 例如：-6
      

综上：
负数的：
十进制变二进制：原码–反码–加一（补码）
二进制变十进制：减一–反码–原码

• 验证负数的二进制转十进制整数的补码操作中反码后减1与加一后反码的值是否一致。

  • eg：将 10010010 转换成整数

  先取反，值为 01101101，再减1，值为 01101100， 十进制为108，对应的原值为 -108

  先减1，值为 10010001，再取反，值为 01101110 ，十进制为 110，对应的原值为 -110。

  另外还看见有一个作者是 先取反再加1的 ，10010010 取反为 01101101，再加1为，01101110，对应的十进制为 110，对应的与原值为 -110， 这样算起来居然也是对的

  然后实践证明，后两种方法都是ok的，虽然有点不太明白，但是为了不混淆，还是只记第二种方法好了，因为第二种方法与负十进制整数转二进制流程刚好相反。

  实验证明这两步操作对换后的值是不一致的，所以谨记，二进制最高为1的时候，对应的十进制整数为负数的时候，二进制转十进制需要先-1在取反，

十六进制

• 十六进制就是每位上可以表示16个，由0~ 9,A~ F，其中A~F分别表示，10 ~15。

进制之间的转换

参考 https://jingyan.baidu.com/article/495ba84109665338b30ede98.html
https://blog.51cto.com/yuanbin/111161
https://www.cnblogs.com/gaizai/p/4233780.html

• 综上总结：以x转十进制为例
  • n进制转十进制， x乘以n的下标次方，再相加
  • 十进制转n进制，x除以n，记录余数，取商继续除以n，直到商0，将余数反向拼接即可
  • 十六进制转n进制，需先将十六进制转换成二进制后再做计算
  • 八进制转十六进制，需先转换成二进制转十六进制的模式，再4位一组，按位乘以2的下标次方，再拼接即可。
  • 二转八，三位一组，按位乘以2的下标次方，拼接即可