pytorch ——线性回归
1.读取数据
2.设定模型和loss function
3.训练模型
设定数据集
先设定好真实的w和b,以及x是什么, y是什么:
true_w = [2, -3.4]
true_b = 4.2
batch_size = 10
为什么w十个二维向量呢?因为设定模型的时候就有两个参数。具体一点说,x1是房屋面积,而x2是房龄。w1和w2是两个参数的权重。得出的y是房屋的售价。

然后我们首先设定x是取一个随机数,但是是二维的,因为x1和x2嘛。
features = torch.randn(1000, 2, dtype=torch.float32)
是一个1000*2的张量。
然后是设定y的值:
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
我们还要增加一个噪声项目,这个噪声项是符合正态分布,均值是0,标准差是0.01。

因为我们要设置成一个近似于直线的数据集,这样才符合真实的情况,然后从这个真实的情况里面拟合出一个线性的方程组。
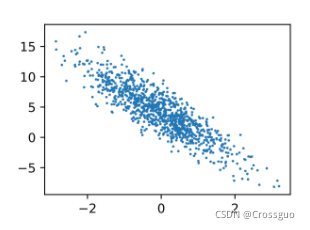
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float32)

读取数据集
def get_data(batch_size, features, labels):
total_num = len(features)
list_result = list(range(total_num))
random.shuffle(list_result)
for i in range(0, total_num, batch_size):
get_list = torch.LongTensor(list_result[i: min(i + batch_size, total_num)])
yield features.index_select(0, get_list), labels.index_select(0, get_list)
把数据集做成一个列表,然后把列表中长度为batch_size的数组取出来,返回这个数组。这个设定的batch_size = 2,所以每个批量返回的特征形状为(10, 2)
初始化模型参数
w = torch.tensor(np.random.normal(0, 0.01, (2, 1)), dtype=torch.float32)
b = torch.tensor(1, dtype=torch.float32)
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
初始化w是一个正态分布的张量,b = 1的张量。
设定模型
def linear_regression(X, w, b):
return torch.mm(X, w) + b
设定优化方法
def loss_function(y_hat, y):
return (y_hat - y.view(y_hat.size())) ** 2 / 2
def grad_step(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size
这个params就是w和b,有两个参数 所以用for循环。除以batch_size是根据公式:

训练模型
lr = 0.03
epochs_num = 10
for epoch in range(epochs_num):
for X, y in get_data(batch_size, features, labels):
l = loss_function(linear_regression(X, w, b), y).sum()
l.backward()
grad_step([w, b], lr, batch_size)
w.grad.data.zero_()
b.grad.data.zero_()
train_l = loss_function(linear_regression(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
这个
loss_function(linear_regression(X, w, b), y).sum()
.sum()是针对公式:

需要求和的。
l.backward()
是反向传播,去更新l中的参数。
简单的线性回归实现
1.生成数据集
跟之前是一样的
num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = torch.tensor(np.random.normal(0, 1, (num_examples, num_inputs)), dtype=torch.float)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float)
2.读取数据就不一样了,不需要自己编写
import torch.utils.data as Data
batch_size = 10
# 将训练数据的特征和标签组合
dataset = Data.TensorDataset(features, labels)
# 随机读取小批量
data_iter = Data.DataLoader(dataset, batch_size, shuffle=True)
先把数据和标签组合,然后加载成小批量返回。
for X, y in data_iter:
print(X, y)
break
可以通过这种方式查看数据与标签的数组,跟之前是一样的。
3.建立模型
net = nn.Sequential(
nn.Linear(num_inputs, 1)
# 此处还可以传入其他层
)
4.初始化参数
from torch.nn import init
init.normal_(net[0].weight, mean=0, std=0.01)
init.constant_(net[0].bias, val=0) # 也可以直接修改bias的data: net[0].bias.data.fill_(0)
5.定义损失函数
loss = nn.MSELoss()
6.定义优化算法
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr=0.03)
print(optimizer)
7.训练模型
num_epochs = 3
for epoch in range(1, num_epochs + 1):
for X, y in data_iter:
output = net(X)
l = loss(output, y.view(output.size()))
optimizer.zero_grad() # 梯度清零,等价于net.zero_grad()
l.backward()
optimizer.step()
print('epoch %d, loss: %f' % (epoch, l.item()))