sklearn逻辑回归参数设置_进击的机器学习 Fifth Day——逻辑回归（Logistic Regression)

提到逻辑回归呢？我一下子就想起了我批判性思维的老师晋逻辑。

算法原理：

首先来声明一下，虽然我们算法的名字就叫做逻辑回归，但是逻辑回归却是一个二分类算法(周志华老师称之为线性几率回归或者对数几率回归),一般只能用来预测含有两种标签（或者类别）的数据，比如0和1，男和女等等。为什么它的名字里面包含了回归呢？我想可能是因为模型中包含了一个线性回归表达式y=w*x+b,这样的话y的取值就有可能非常大，也有可能非常小，这样怎么能用于分类呢？于是Sigmoid函数就出现了，函数表达如下：

可以看出Sigmoid函数的定义域是整个空间，而它的值域处于0（自变量趋于负无穷大）和1（自变量趋于正无穷大）之间，我们将y的取值作用于Sigmoid函数得即到如下关系：

也就意味着我们把y值映射到另一个空间，通过映射的结果（ P(Y=1|x)表示映射结果Y等于1的概率）和0.5的大小关系，我们从而来预测类别（和标签）。Tips:逻辑回归一般只适合用于二分类，但是也存在一对多One-Vs-Rest(One For All ?)和多元逻辑回归（Multinomial Logistic Regression)用于多类别的回归。

算法背后的数学推导

1、Sklearn的逻辑回归

#这次的文件和KNN文件相同，不再重复介绍
#这是一个简单的二元分类逻辑回归模型
#导入必须的库
from sklearn.linear_model import LogisticRegression as LR#唯一的不同在这
from sklearn.preprocessing import StandardScaler as SS
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.preprocessing import LabelEncoder as LE 
import pandas as pd
import numpy as np
dataset=pd.read_csv(path)
x=dataset.iloc[:,1:4].values
y=dataset.iloc[:,4].values
x[:,0]=LE().fit_transform(x[:,0])
x=SS().fit_transform(x)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=0)
#以上是数据的预处理
model=LR(random_state=0)#模型实例化
model.fit(x,y)#拟合x,y
y_pre=model.predict(x_test)#预测
accuracy=confusion_matrix(y_test,y_pre)#计算混淆矩阵
print(accuracy)

当然Sklearn还可以用来生成可以用来分类多标签的逻辑回归模型，代码只需要做稍微的改动

model=LR(multi_class='ovr')#这个是One For All
#或者
LR(multi_class='multinomial')

其次也可以对模型进行正则化，防止过拟合需要导入
sklearn.linear_model.LogisticRegressionCV
,对这个类进行实例化的时候可以设置正则化参数；如果要对大量数据进行处理可以在LR中加入参数
solver='sag'
(平均梯度下降）；如果数据不均衡（也就是说每个类的数目差异很大）可以设置LR中的
class_weight='balanced'

以上所有即为Sklearn的逻辑回归模型，如果只是要求用的话我觉得已经足够了，但是要想真正的理解还是得TensorFlow和Numpy出马。

2、TensorFlow搭建逻辑回归模型

#TensorFlow搭建逻辑回归模型
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler as ss
epoch=5000
dataset=pd.read_csv(r'C:UsersykDesktoppython机器学习数据可视化文本test_day6.csv')
x=dataset.iloc[:,2:4].values
y=dataset.iloc[:,4:].values#记好教训，以后的数据都用二维格式
x=ss().fit_transform(x)
#以上为数据的预处理
X=tf.placeholder(tf.float32,x.shape)
Y=tf.placeholder(tf.float32,y.shape)#创建x,y的占位符，注意我们用的都是二维张量
w=tf.Variable(tf.zeros((2,1)))
b=tf.Variable(tf.zeros(1))#创建变量w和b
equation=tf.matmul(X,w)+b#创建回归函数
sigmoid=tf.sigmoid(equation)#创建Sigmoid函数
cost=Y*tf.log(sigmoid)+(1-Y)*tf.log(1-sigmoid)#创建损失函数
cost_entropy=-tf.reduce_sum(cost)/len(x)#创建交叉熵函数
learning_rate=0.001#设置学习率
epoch=100000#设置学习次数
optimizer=tf.train.GradientDescentOptimizer(learning_rate).minimize(cost_entropy)#设置优化器，选用梯度下降的方法
init=tf.global_variables_initializer()
feed_dict={X:x,Y:y}#设置喂养数据
cost_list=[]#记录损失函数值
with tf.Session() as sess:#开辟一个会话窗口
    sess.run(init)#对变量进行初始化赋值
    for i in range(epoch):
        sess.run(optimizer,feed_dict)#进行梯度下降
        W=sess.run(w,feed_dict)#计算w
        B=sess.run(b,feed_dict)#计算b
        cost_value=sess.run(cost_entropy,feed_dict)#计算损失函数值
        cost_list.append(cost_value)#记录损失函数变化
        if i%100==0:
            print(i,'==>','Cost=',cost_value,'w=',W,'b=',B)#可视化
    sess.close()
plt.plot(np.arange(1,epoch+1),cost_list)#绘出损失函数收敛情况
plt.show()
for i,j in zip(x,y):
    if j==0:
        plt.scatter(i[0],i[1],c='r',marker='o')
    else:
        plt.scatter(i[0],i[1],c='b',marker='x')

损失函数收敛情况

3、自己动手搭建逻辑回归模型，俗话说自己做才是最香

#自己动手写逻辑回归
import numpy as np
from sklearn.preprocessing import StandardScaler as ss
import pandas as pd
import matplotlib.pyplot as plt
dataset=pd.read_csv(r'C:UsersykDesktoppython机器学习数据可视化文本test_day6.csv')
x=dataset.iloc[:,2:4].values
y=dataset.iloc[:,4:].values
x=ss().fit_transform(x)
#数据预处理
def sigmoid(x):
    return 1/(1+np.power(np.e,-x))
#定义Sigmoid函数
def logistic_Gradient(x,y,epoch,alpha):#定义逻辑回归梯度下降；参数x,y表示数据集，x为400*2，y为400*1;epoch表示学习次数；alpha表示学习效率
    w=np.ones((x.shape[1],1))
    b=np.zeros((1,1))#对w和b赋予初值
    cost_list=[]#记录损失函数变化值
    for i in range(epoch):
        cost=compute_cost(x,y,w,b)#首先计算损失函数值
        cost_list.append(cost[0,0])#加入到列表中
        print(cost[0,0])
        error=y-sigmoid(np.matmul(x,w)+b)
        dt_w=(-1/len(x))*np.matmul(x.T,error)
        dt_b=(-1/len(x))*error.sum()
        w-=alpha*dt_w
        b-=alpha*dt_b#上面是迭代公式参见讲解，就是对函数求偏导后得到的结果
    return (w,b,cost_list)
def compute_cost(x,y,w,b):#计算损失函数值，算法原理讲解部分有公式
    h=sigmoid(np.matmul(x,w)+b)
    return (-1/len(x))*(np.matmul(y.T,np.log(h))+np.matmul(1-y.T,np.log(1-h)))
if __name__=="__main__":
    w,b,cost=logistic_Gradient(x,y,10000,0.01)
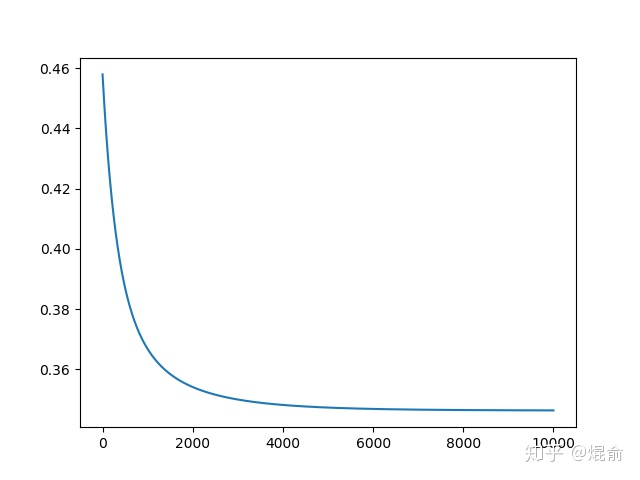
    plt.plot(np.arange(1,len(cost)+1),cost)#绘制损失函数变化情况
    plt.show()

看看损失函数收敛结果

你可能也喜欢