背景介绍
某天,要重新编译一个超级大工程。漫长的加载和编译时间至少要等一个上午,让我们来做一些有趣的事情吧。
前段时间,测试同学报了一个BUG,游戏比分没办法严格精确到小数点后面两位。
策划的需求是,
如果数字小数点后面超出两位,直接进行数字截取前两位,不能做任何四舍五入之类的操作。例如,1.9999必须为1.99,不能变成2.00。
首先查阅框架代码,乍一看,确实也对这种情况进行了处理。
function Format2(val)
local tempVal = tonumber(val)
local nTemp = tempVal * 100
local nVal = tonumber(string.format("%.2f", nTemp / 100))
return nVal
end但是其实这段代码有大问题,甚至可以说基本是无效代码。
哪里出了问题呢?
请教同事查阅博客,虽然找到了一些细碎的线索,但是没有人给出一个精确地,完整的答案,或者令人信服的理论依据,那么自己来测试一下吧。
三种方案的代码分析
讨论这个问题之前,首先要明确一个问题,lua的number类型,是默认当成双精度浮点类型来运算的。也就是说number会底层当做double类型来处理,精度是16~17位 。
框架中原有的方案
Ps:对原有代码脱敏处理,保留该问题的关键逻辑,并且为了方便测试,将精度改为了1位。
function Format2(val)
local tempVal = tonumber(val)
local nTemp = tempVal * 10
local nVal = tonumber(string.format("%.1f", nTemp / 10))
return nVal
end
这里应该是模拟C++的用法,只不过用法有问题。
以一位精度为例,C++中,先tempVal*10,此时结果是double类型,然后强转为int类型,就可以把小数位切掉,再除以10既可实现截取一位精度小数
。
但是Lua中所有的数字全都都是浮点型,没有精度转换的概念。所以这里替换成了string.format(“%.1f”,s),
不过lua的string.format(“%.1f”,s)其实是有个的“四舍六入五成双”逻辑的。PS:网上大多数人说是四舍五入,是有错误的。
也就是说这一段代码根本不能满足需求,不知道为什么这个BUG隐藏了这么久。
什么是四舍六入呢
(1)被修约的数字小于5时,该数字舍去;
(2)被修约的数字大于5时,则进位;
(3)被修约的数字等于5时,要看5前面的数字,若是奇数则进位,若是偶数则将5舍掉,即修约后末尾数字都成为偶数;若5的后面还有不为“0”的任何数,则此时无论5的前面是奇数还是偶数,均应进位。
string.format(“%.1f”, num)的四舍六入验证
测试代码
function StringFormat(val)
return string.format("%.1f", val)
end
-- 防盗水印:本文原创https://blog.csdn.net/lanazyit/article/details/111051387
测试数据输入
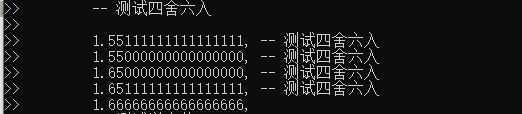
输出
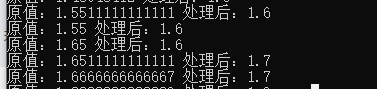
原值:1.5511111111111 处理后:1.6
分析
— 原值1.5
5
,
5
后面有值,进了一位
原值:1.55 处理后:1.6
分析
— 1.
5
5
—
5
后面没有值,但是
5
前面还有个奇数
5
,进了一位。
原值:1.65 处理后:1.6
分析
— 1.6
5
—
5
后面没有值,但是
5
前面有个偶数6,舍弃。
防盗水印:本文原创
https://blog.csdn.net/lanazyit/article/details/111051387
使用math.floor模拟进制转换的方案
我看到这个BUG时,第一想法:
使用math.floor模拟一下double到int的强转逻辑就可以了。
function Format3(val, n)
local n = math.pow(10, n or 1)
val = tonumber(val)
return math.floor(val * n) / n
end后续验证发现,这个方法确实能用。
但是math.floor一定靠谱么?
PS:最初有这个疑惑,是因为看了这个
前辈的博客
math.floor一定靠谱么?
这个问题其实不难理解,不过我们还是来验证一下吧。
function FormatFloor(val)
return math.floor(val)
end先看一组测试数据。
输入值

输出值
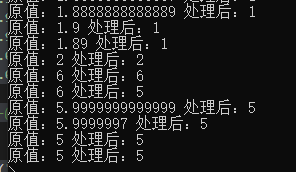

注意一下,从第四个数据1.99999999999999999开始,结果就出现不同程度的“错误”,比如我们输入1.99999999999999999,向下取整却得到了2。
不过这里并不能说明math.floor是异常的。
因为这里其实是浮点型的机制引起的”理解偏差”,浮点型在内存中其实是一个2进制的分数(C#本质论,值类型那一章有详细讲解,一般的C++书应该也会讲),我们将其转换成十进制进行输出或者其他运算操作时,2进制分数和十进制小数无法严格一一对应,所以会有一个取近似值的操作,特别是精度值溢出后,甚至会直接做四舍五入和截取的操作。

所以这里其实不是math.floor问题,而是lua直接将1.99999999999999999,直接当成了2来处理(注意第一个tostring输出时,已经将原值认为成2了)。那么1.99999999999999999在lua中被识别成了2,math.floor截取也是2,结果还是正确的。
毕竟应该不会真的有人同学过分到把double精度溢出到如此地步,再做运算吧。
专门写C++服务器的兄弟告诉我,1.999999999999999999这种值,不要考虑什么近似操作,它就是2。不管是计算机,还是我们自己阅读时,都应该将它当做2来对待,这样会省去很多麻烦。
然后我们再来考虑一个问题,我们能否不使用强行转精度的方式,来实现截取效果呢?
不使用强行转精度方式的方案
对原数字进行取余的操作,然后把余数减掉,也可以来实现这种需求。
这种操作的好处是,过程中没有任何强转,虽然每次运算都有可能出现取近似值的操作,但是完全将这些近似和转换交给底层来做,却往往比我们自己瞎操作得到的结果更理想更安全。
不过这里就仁者见仁智者见智吧。
-- 不截取任何精度截取
function Format4(val, n)
local n = math.pow(10, n or 1)
val = tonumber(val)
val = val * n
val = val - val % 1
return val / n
end
我希望1.999999999999999999不要变成2?
如果策划再提一个变态需求,我希望1.999999999999999999不要变成2,那怎么办呢。
经过多次试验,答案是,转成字符串再进行操作。即,
输入的时候就传进来字符串,不要让内存做任何精度相关的处理。然后使用字符串截取来完成截取操作。
function Format5(val, n)
n = n or 1
local tempVal = tostring(val)
-- local startIndex,endIndex = string.find(tempVal, ".") -- 这里有个很严重的BUG,刚好与正则表达式冲突了
local startIndex, endIndex = string.find(tempVal, ".", 1, true)
if startIndex and startIndex > 0 then
if startIndex + n < string.len(tempVal) then
return tonumber(string.sub(tempVal, 1, startIndex + n)) -- 两位精度是3
else
return tonumber(string.sub(tempVal, 1, string.len(tempVal)))
end
else
return tonumber(val)
end
end看似简单,这里遇到了一个坑。为了找到小数点的位置,我使用了string.find(tempVal, “.”)来查找,但是这个参数string.find竟然默认是正则表达式识别的。传入一个“.”,相当于会识别所有的字符。导致结果一直输出错误。
-- local startIndex,endIndex = string.find(tempVal, ".") -- 这里有个很严重的BUG,刚好与正则表达式冲突了
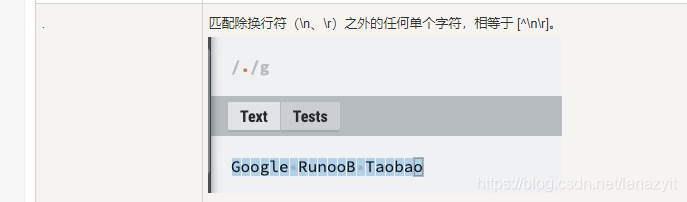
正确的参数填写如下,如此便可以不适用正则表达式,强行”.”匹配。
local startIndex, endIndex = string.find(tempVal, ".", 1, true)看官老爷,文章对你有帮助嘛,点个赞可以嘛。攒攒人气,谢谢啦。