博客

知识点：理解对角线与熟悉二维数组的下标。

二维数组本质上是以数组作为数组元素的数组，即“数组的数组”，类型说明符 数组名[常量表达式][常量表达式]。二维数组又称为矩阵，行列数相等的矩阵称为方阵。

触类旁通，相信大家在了解完一维数组后，对二维数组也有某种程度上的理解。

既然一位数组的下标是从0开始的，那么必然，二维数组也是一样。

但有区别的是，二维数组在一维数组原有的基础上增加了行和列，因此它的下标便从【0】变为【0】【0】，也就是一个元素的下标。所以，想要学会数组，就要能够灵活的使用下标。

陈述问题

：计算二维数组主对角线元素和与辅对角线元素和。

分析问题：

1. 只有行列数相等的情况下，才有对角线，也就是被称之为方阵。想要计算对角线元素和，就得找出在对角线上的元素。

2. 引入图片进行分析
   

3. 这是一张3*3的矩阵图。通过这张图，想必大家能够清晰的认知什么是主对角线什么是辅对角线；

4. 对于规律也是显而易见，主对角线是从下标为【0】【0】的元素进行行列顺序递增的一条线；辅对角线是从【0】【2】到【2】【0】，它的规律就是行递增、列递减。但是这张图的数据并不是很能体现出。因此我们再引进一张辅对角线图：
   

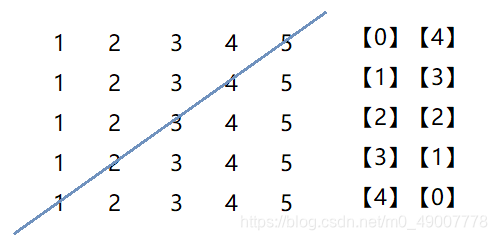
5. 右边数字便是二维数组辅对角线元素的下标，它的规律就是这样来的，行递增，列递减。

6. 所以通过分析画图能使我们更好的理解一道题，在此希望大家养成这样的习惯，在编程的路上越走越远，并收获满满，共勉！

解决问题

代码演示

#include<iostream>
using namespace std;
int main()
{
	int arr[3][3];
	int sum = 0;
	int sum1 = 0;
	//用sizeof求出总列数
	int len = sizeof(arr[0]) / sizeof(arr[0][0])-1;
	cout << "请输入一个三行三列的二维数组：" << endl;
	//用for循环输入数组
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> arr[i][j];
    //循环遍历数组
	for (int i = 0; i < 3; i++)
	{
		for (int j = 0; j < 3; j++)
			cout << arr[i][j]<<" ";
		cout << endl;
	}

     //求主对角线元素和
	for (int i = 0; i < 3; i++)
	{
		int j = i;
		sum += arr[i][j];
	}
	cout << "主对角线和： "<<sum<<endl;
	
	//求辅对角线元素和
	int i=0 ,j=len;
	while (true)
	{
		sum1 += arr[i][j];
		i++;
		j--;
		if (j < 0 || i>2)
			break;
	}
	cout << "辅对角线和：" <<sum1<< endl;
	return 0;
}

请输入一个三行三列的二维数组：

1 2 3 4 5 6 9 8 7

1 2 3

4 5 6

9 8 7

主对角线和： 13

辅对角线和：17