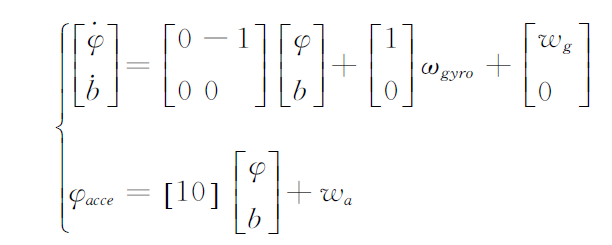链接:
https://blog.csdn.net/haishaoli/article/details/52965457
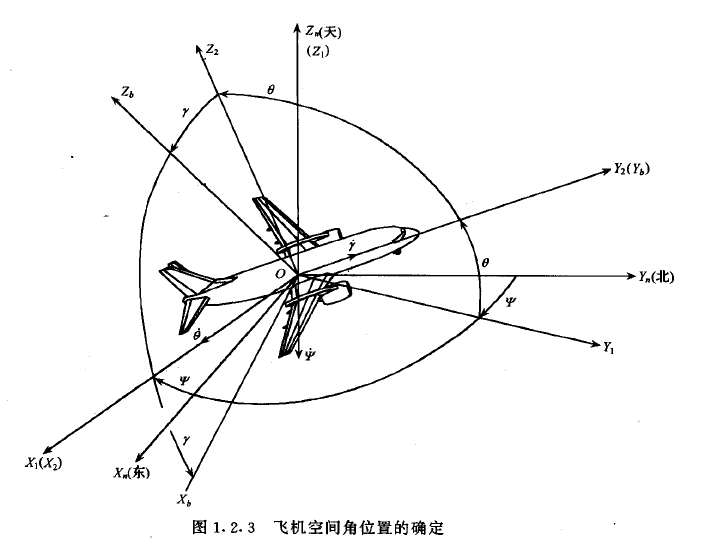
目的:我们需要得到机器人运动的姿态信息,三个轴的角度以及角速度。
本文大纲:
1、传感器相关模型
2、坐标变换
3、经验型卡尔曼数据融合
4、姿态解算流程
5、DMP
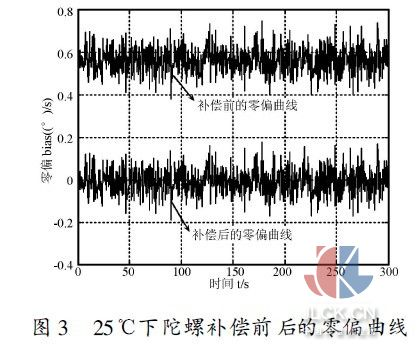
6、数据融合效果
本文出处:http://blog.csdn.net/haishaoli/article/details/52965457
本文内容:
姿态解算总框图(欧拉角方式):
一、数据模型、 噪声模型及曲线
1、欧拉角定义:
2、数据模型:
其中,φ表示的是测量的角度,b表示的是陀螺仪的飘移误差(为常值偏差),ωgyro表示的是陀螺仪的角速度输出值。ωg为陀螺仪测量噪声,φacce为加速度计经过处理后得到的角度值,ωa为加速度计测量噪声。
噪声模型近似为高斯分布,如下图:
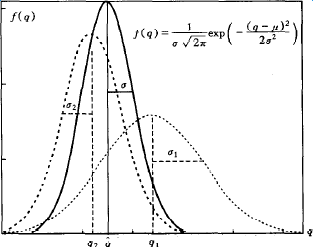
A、加速度计噪声图

B、陀螺仪噪声图
二、 坐标变换(欧拉角方式):把陀螺仪角速度变换到加速度计的地理坐标系上
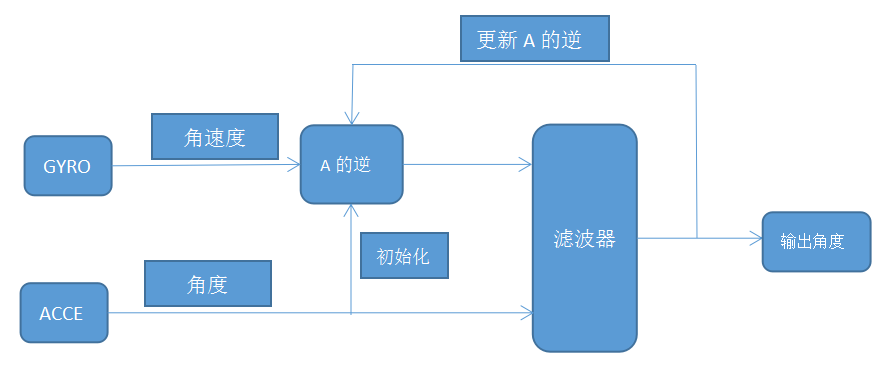
1、陀螺仪数据的使用:
A的逆:其中A矩阵为姿态矩阵。
下面内容来自《惯性导航》:主要是把三轴角速度从机体坐标系换算到地理坐标系上。
使用上述公式,在只使用陀螺仪的条件下,可以求得地理坐标系下的三轴角速度信息。
角速度进行积分,就能得到相应的角度信息。
2、加速度计数据的使用:
使用上述公式,在只使用加速度计的条件下,可以求得俯仰角和横滚角信息。
三、 卡尔曼数据融合
A、 融合效果:本文最后附图。
B、一行代码:
a = (1 – d%) * b + d% * c;
a 是 融合输出 ,b 是预测量,c 是观察量
这是关键的融合代码。
C、提问:
上述代码的含义是什么?
加权平均?互补滤波?低通高通滤波器?
同样的式子,不同的使用过程,有不同的意义。
如果系数是一个固定的值,则有可能是加权平均或者高通低通滤波器。
我讲的是动态的系数。获取数据在变,方差(或协方差)在变,系数就在变。
D、理解:
1、什么情况使用 ? 高斯分布。
单模、零均和、高斯噪声 (高斯白噪声)。之前说明了传感器的噪声属于白噪声。
2、卡尔曼为什么是最佳估计 ?下面使用最小二乘来理解。
推导方式一:
q1 是预测量,q2是观察量,q是估计值,w是权值。下文来自《自主移动机器人导论》。
其中q1和q2的系数之和为1。
利用这种推导方式可说明卡尔曼是最佳估计,但是并不能推出方差的表达式,并且,权值Wi还是我们自己取的。
推导方式二:
运用贝叶斯定理推导:推出融合表达式和方差表达式
3、卡尔曼的核心。 方差,或者说权重。其实就是卡尔曼增益。
方差公式,跟电阻类似,结果比原来两者都小。因此就算是预测量的累积误差较大,也能提高系统的精度,误差通过迭代而减少。这说明了该方法的有效性。
4、获得卡尔曼增益的方式对比:
自动通过统计和计算数据方差 VS 人为经验估计方差 的对比 :
1、自动需要高频数据,人为经验不用。
2、自动具有通用性,人为特定性。
3、自动计算量大,人为的计算量较少。
从5.35可推出:q = (d%) * q1 + (1-d%) * q2;
5、应用:我们的姿态融合,定位融合都是人为给出卡尔曼增益系数的,叫做“经验型卡尔曼滤波”。
经验之谈:
A、参数一般是给的很小,原因跟传感器(数据)的误差模型相关;
参数小的原因:分析卡尔曼增益的式子,预测量的方差较小,观测量的方差较大,不是同一个数量级,因此增益系数一般给的很小;见定位融合图,可看出方差情况。
B、“经验型卡尔曼滤波”的核心思想是变化卡尔曼增益系数;根据经验我们能知道哪些条件下传感器数据的方差大,哪些条件下方差小,从而改变增益系数。
C、融合线程的频率越高越好。频率高,一方面收敛快,另外一方面获得的预测量误差小。
四、 姿态解算流程
以下是以数据流的方式去理解。
1、传感器原始数据输入。
2、传感器标定,方法很多,比如六面法。把标定后的数据换算成标准单位。
3、确定坐标轴和数据符号,符号用右手定则。
4、欧拉角变换或者四元数变换,变换是为了使陀螺仪角速度的坐标系与加速度计的坐标重合。
5、数据融合,减小方差,降低噪声。
6、输出融合后的姿态信息。
五、 DMP
这是MPU6X00芯片的自带功能。不开源。
性能还不错,甚至更好。计算有一部分是利用IMU自身的资源,不过依赖芯片产商。
六、数据融合实验效果:
A、 姿态融合效果:蓝色的线是融合输出。平滑并且响应快。
B、定位融合效果:绿色的线是融合输出,蓝色的线是观测量,红色是预测量。
———————
作者:AutoSlam
来源:CSDN
原文:https://blog.csdn.net/haishaoli/article/details/52965457
版权声明:本文为博主原创文章,转载请附上博文链接!