目录
1. Hough 直线检测
霍夫变换(Hough 变换):利用对偶原理,把原空间的问题转换到对偶空间去求解
这里涉及到空间转换,将原来的笛卡尔空间(xy空间)转换到参数空间(霍夫空间)
例如:笛卡尔空间上的一个
位置确定
的点(x0,y0),经过这个点的直线方程为:y0= k * x0 + b。这里可以知道,由于k、b的不确定性,因此这个直线是无数条
将笛卡尔空间上的方程进行简单变换 b = – x0 * k + y0 的形式(这里新的坐标轴是k、b,也叫参数空间或者霍夫空间)。由于(x0,y0)是已知的,(k、b)是未知的参数,那么在笛卡尔空间就是一个确定的点(
想象这个点是由无数条直线相交同一点确定的
)。因此在参数空间,就是一条斜率为-x0,截距为y0的直线(
k、b未确定,因此在参数空间,是kb定义域是R的一条直线
)。所以,我们得出的结论是:
笛卡尔空间上面的一个确定点,对应参数空间(霍夫空间)上的一条确定的直线
例如:笛卡尔空间(x0 = 1,y0 = 2),那么在笛卡尔空间由无数条直线相交于同一点的方程是:y = k(x – 1) + 2 = k*x + 2-k(这里2-k是b)
因此在参数空间是: 2-k = -x * k + y ——> b = -x * k + y—-带入(1,2)—–> b = -k + 2

如果,笛卡尔空间上还有一点(x1,y1)的话,那么这一点也对应一条参数空间的一条直线。并且在笛卡尔空间,由于两点必可以确定一条直线,因此在参数空间的效果就是,两条直线必相交于一点。可以得出结论:
笛卡尔空间的一条直线,对应参数空间(霍夫空间)上的一个确定的点
例如:笛卡尔空间的两个点(1,2)(2,3)
- 点(1,2)在笛卡尔空间y = kx + 2-k ,转到参数空间为2-k = -xk + y,带入(1,2)得:b = 2-k = -x*k+y = – k + 2
- 点(2,3)在笛卡尔空间y = kx + 3- 2k ,转到参数空间为3-2k = -xk + y,带入(2,3)得:b = 3 – 2k = -x*k+y = -2 * k + 3
在笛卡尔空间两点得到的直线方程为:y = x + 1
在参数空间两条直线得到的交点为:k = 1 ,b = 1
笛卡尔空间直线的k、b,就是参数空间点的坐标(k,b)

所以,如果需要做直线检测的话,将笛卡尔空间上的点映射到参数空间对应一条直线。然后如果映射前,笛卡尔空间点在一条直线上的话,那么对应参数空间直线就会相交到同一点上。
因此,图像上主要直线可以通过标识参数空间中大量直线相交的点来确定
上述的变换是可行的,但是有个缺点是,当笛卡尔空间是垂直的直线是,对应参数空间的k是无穷大的,且截距b无法取值。解决的思路是将参数空间改为极坐标空间,将直线转为(r,θ)空间多个曲线的交点

2. HoughLinesP 函数

- 返回值格式为:[[[x1,y1,x2,y2]]]
代码:
import numpy as np
import cv2
img = cv2.imread('./chessboard.png',1) # 读取图像
img = cv2.GaussianBlur(img,(7,7),sigmaX=1) # 高斯模糊图像
img_bin = cv2.Canny(img,50,100) # 得到二值图像
lines = cv2.HoughLinesP(img_bin,1,np.pi / 180,threshold= 10) # Hough 变换
for line in lines:
x1,y1,x2,y2 = line[0] # 提取线段
cv2.line(img,(x1,y1),(x2,y2),(0,0,255),1) # 在原图上绘制线段
cv2.imshow('Canny',img_bin) # 显示 Canny 检测的图像
cv2.imshow('img',img)
cv2.waitKey()
cv2.destroyAllWindows()
处理结果为:
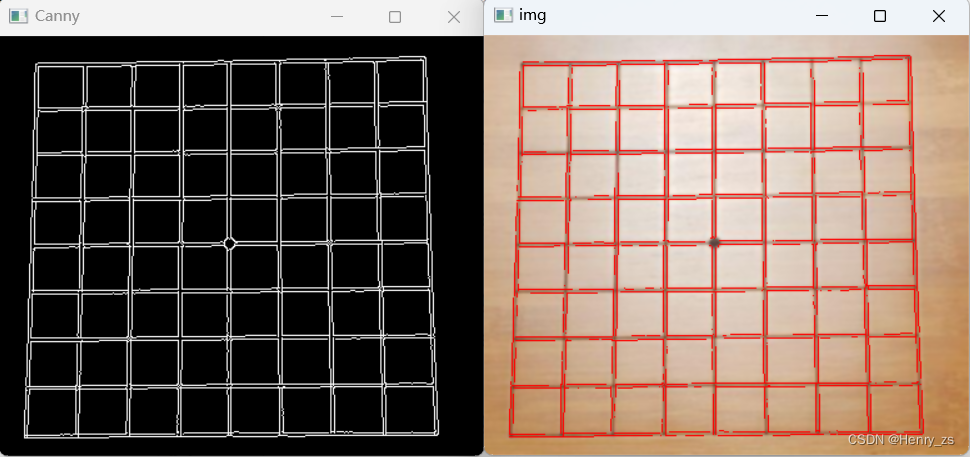
这里的lines 返回的shape是(n,1,4),n代表n条直线,(1,4)是一行四列每个线段的起点和末端点
所以line去迭代lines,就得到(1,4)的line,然后line[0] 就可以将起点、终止点取出来