基本单位换算:
1G=》1024*1024*1024=》1 000 000 000=》10亿
10亿整数=》1G整数=》1G*4字节=》4GB(32位int占4字节,int*4字节,64位int4字节,int*8字节)
50亿整数=》5G整数=》5G*4字节=》20GB(32位)
海量数据查重/去重
有一组IP地址、URL、字符串,哪些有重复,重复了多少次,去除重复的
考虑类似这种问题,主要有以下思路:
- 哈希表 + 分治思想:哈希表增删查O(1),但是占空间大,10亿个整数,大约占4GB,用哈希表存key-value,空间翻一番
- Bloom Filter:布隆过滤器(纯粹查重用的)
- 字符串类型还可以用TrieTree字典树(前缀树)
1.给你一万个数字,怎么统计重复的数字?
思路:
- 遍历数组,使用无序单重哈希表unordered_map存储 [数字-重复次数]
#include <unordered_map>
#include <iostream>
using namespace std;
int main()
{
//问:给你一万个数字,怎么统计重复的数字?
const int SIZE = 10000;
int arr[SIZE] = { 0 };
for (int i = 0; i < SIZE; ++i)
{
arr[i] = rand();
}
//答:使用unordered_map,key-重复次数
unordered_map<int, int> map;
for (int val : arr)
{
map[val]++;
}
for (auto pair : map)
{
if (pair.second > 1)
{
cout << "数字:" << pair.first << " 重复次数:" << pair.second << endl;
}
}
}
2.有一个文件,有50亿个整数(占20GB),最多可使用的内存是400M,让你找出文件中重复的元素以及重复次数
思路:
- 分治思想:大文件划分成小文件,使得每一个小文件能够加载到内存当中,求出对应的重复元素,把结果写入到一个存储重复元素的文件当中
- 大文件=》小文件个数(40G/400M =》120个小文件左右)
-
data0.txt
data1.txt
data2.txt
…
data126.txt - 遍历大文件的元素,把每一个元素根据哈希映射函数,放到对应序号的小文件当中data % 127 = file_index
海量数据topK
给你10亿个整数,求出值最大的前10个、求出值第10大的数字
求最大的/最小的前k个元素
求最大的/最小的第k个元素
解法1:大根堆=》找topK小的,小根堆=》找topK大的
-
大根堆:
找最小的前k个元素,找小的就要淘汰大的,所以用大根堆(堆里的是未淘汰的)
。先用开始的k个元素创建大根堆(大值在堆顶),然后遍历剩下的元素,比堆顶大,继续遍历,比堆顶小,堆顶出堆,该元素入堆,调整堆,遍历完所有的元素,大根堆里存的就是最小的前k个元素 -
小根堆:
找最大的前k个元素,找大的就要淘汰小的,所以用小根堆(堆里的是未淘汰的)
。先用开始的k个元素创建小根堆(小值在堆顶),然后遍历剩下的元素,比堆顶小,继续遍历,比堆顶大,堆顶出堆,该元素入堆,调整堆,遍历完所有的元素,小根堆里存的就是最大的前k个元素 - 如果找的是第k小的(大根堆堆顶)或者第k大的(小根堆堆顶),只需要访问堆顶一个元素就可以了
- priority_queue底层默认是大根堆
代码示例
vector容器中有10 0000个数字,求vector容器中元素值最大的前10个数字
#include <vector>
#include <queue>
#include <iostream>
using namespace std;
int main()
{
vector<int> vec;
for (int i = 0; i < 100000; ++i)
{
vec.push_back(rand() + i);
}
// 算法的时间复杂度:O(n)*O(log_2_10) => O(n)
// 定义小根堆
priority_queue<int, vector<int>, greater<int>> minHeap; //大根堆:priority_queue<int> maxHeap;
// 先往小根堆放入10个元素
int k = 0;
for (; k < 10; ++k)
{
minHeap.push(vec[k]);
}
//遍历剩下的元素依次和堆顶元素进行比较,如果比堆顶元素大,那么删除堆顶元素,把当前元素添加到小根堆中,
//元素遍历完成,堆中剩下的10个元素,就是值最大的10个元素
for (; k < vec.size(); ++k)
{
if (vec[k] > minHeap.top()) // O(log_2_10)
{
minHeap.pop();
minHeap.push(vec[k]);
}
}
// 打印结果 这个是找前K个,如果是找第K个,那么只打印堆顶元素就可以了
while (!minHeap.empty())
{
cout << minHeap.top() << " ";
minHeap.pop();
}
cout << endl;
}
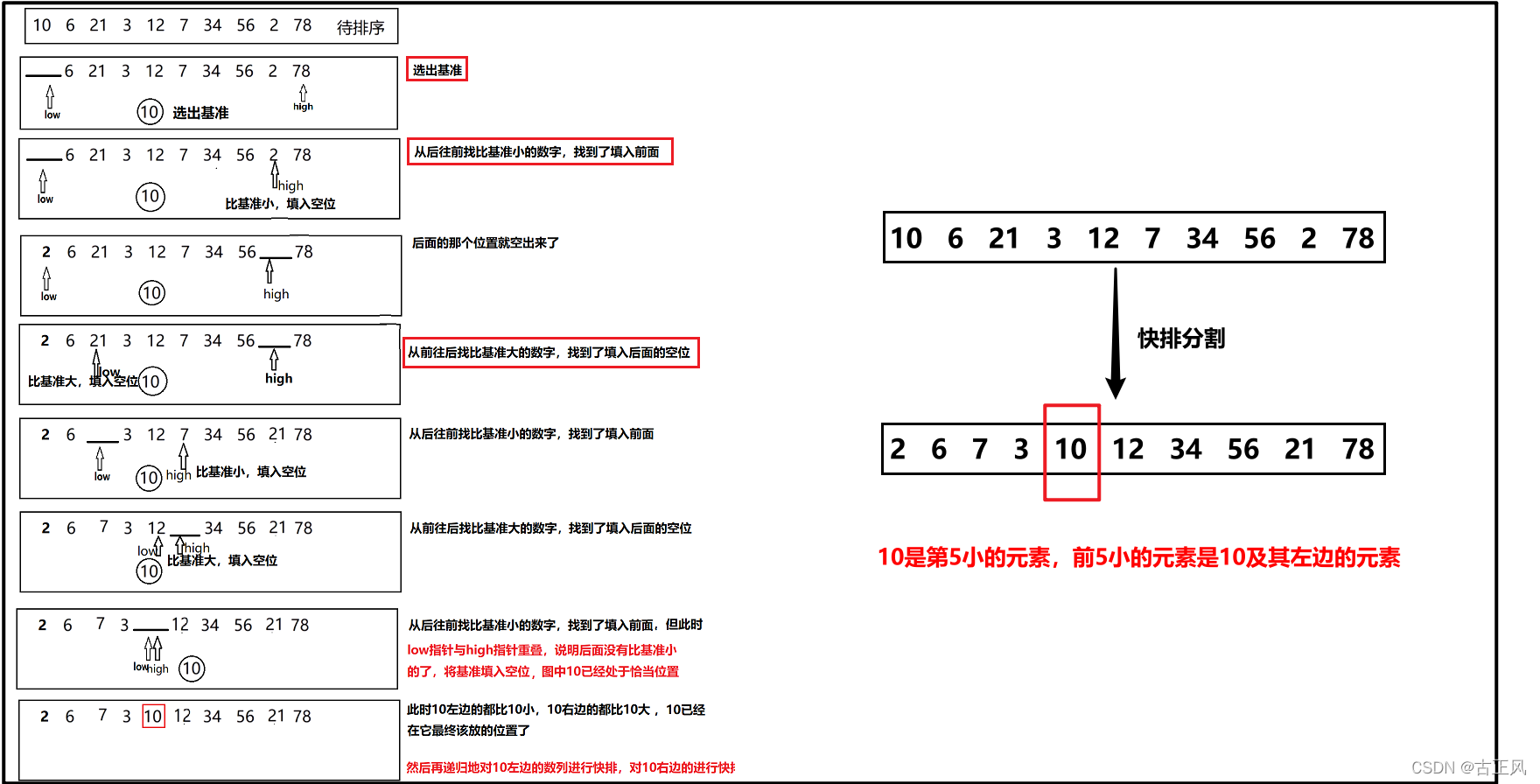
解法2:快排分割函数(一趟快排,把一个数放在它最终的位置)
-
经过快排分割函数,能够把小于基准数的整数调整到左边,把大于基准数的整数调整到右边,
基准数(下标index)就可以认为是第index+1小的整数了,[0, index]就是前index+1小的整数
- 平均时间复杂度:O(n)数学证明的,最坏O(n^2)
代码示例
vector容器中有10 0000个数字,求vector容器中元素值第10小的元素
快排分割函数
//快排分割函数:一趟快排
int partation(vector<int> &nums, int low, int high)
{
//选取一个基准(nums[0]),然后从后往前遍历,找到比基准小的填入,然后再从前往后遍历,找到比基准大的,填入
int base = nums[low];
while(low < high)
{
//从后往前遍历,找到比基准小的填入
while(high > low && nums[high] >= base)
{
high--;
}
if(nums[high] < base)
{
nums[low++] = nums[high];
}
//从前往后遍历,找到比基准大的填入
while(low < high && nums[low] <= base)
{
low++;
}
if(nums[low] > base)
{
nums[high--] = nums[low];
}
}
nums[low] = base;
return low; //返回基准数的最终位置
}
selectNoK函数
//找到arr中第k小的元素并返回其下标
int selectNoK(vector<int> &arr, int start, int end, int k)//start起始下标,end结束下标,k是要找的第几小的
{
int pos = partation(arr, start, end);
if(pos == k-1)
{
return pos;
}
else if(pos < k-1)
{
return selectNoK(arr, pos+1, end, k);
}
else
{
return selectNoK(arr, start, pos-1, k);
}
}
主函数
int main()
{
vector<int> vec;
for(int i = 0; i < 100000; ++i)
{
vec.push_back(rand() + i);
}
//selectNoK返回第10小的元素的下标
int pos = selectNoK(vec, 0, vec.size() - 1, 10);
cout<<vec[pos]<<endl;
//如果要找前10小的元素,访问下标为0-pos之间的元素
for(int i = 0; i <= pos; ++i)
{
cout<<vec[i]<<" ";
}
cout<<endl;
}
综合应用
在一组数字中 ,找出重复次数最多的前10个
- 统计所有数字的重复次数,key:数字的值,value:数字重复的次数
- 用小根堆找value里的topK
// 在一组数字中 ,找出重复次数最多的前10个
int main()
{
// 用vec存储要处理的数字
vector<int> vec;
for (int i = 0; i < 200000; ++i)
{
vec.push_back(rand());
}
// 统计所有数字的重复次数,key:数字的值,value:数字重复的次数
unordered_map<int, int> numMap;
for (int val : vec)
{
/* 拿val数字在map中查找,如果val不存在,numMap[val]会插入一个[val, 0]
这么一个返回值,然后++,得到一个[val, 1]这么一组新数据
如果val存在,numMap[val]刚好返回的是val数字对应的second重复的次数,直接++*/
numMap[val]++;
}
// 先定义一个小根堆 数字=》重复的次数
using P = pair<int, int>;
using FUNC = function<bool(P&, P&)>;
using MinHeap = priority_queue<P, vector<P>, FUNC>;
MinHeap minheap([](auto &a, auto &b)->bool {
return a.second > b.second; // 自定义小根堆元素的大小比较方式
});
// 先往堆放10个数据
int k = 0;
auto it = numMap.begin();
// 先从map表中读10个数据到小根堆中,建立top 10的小根堆,最小的元素在堆顶
for (; it != numMap.end() && k < 10; ++it, ++k)
{
minheap.push(*it);
}
// 把K+1到末尾的元素进行遍历,和堆顶元素比较
for (; it != numMap.end(); ++it)
{
// 如果map表中当前元素重复次数大于,堆顶元素的重复次数,则替换
if (it->second > minheap.top().second)
{
minheap.pop();
minheap.push(*it);
}
}
// 堆中剩下的就是重复次数最大的前k个
while (!minheap.empty())
{
auto &pair = minheap.top();
cout << pair.first << " : " << pair.second << endl;
minheap.pop();
}
return 0;
}
有一个大文件,内存限制200M,求文件中重复次数最多的前10
思路:
-
大文件 散列=》小文件
-
大文件里面的数据 =》哈希映射=》把数据离散的放入小文件当中
-
小根堆找最多的前10个
// 大文件划分小文件(哈希映射)+ 哈希统计 + 小根堆(快排分割)
int main()
{
//先制造一个大文件
FILE *pf1 = fopen("data.dat", "wb");
for (int i = 0; i < 20000; ++i)
{
int data = rand();
fwrite(&data, 4, 1, pf1);
}
fclose(pf1);
// 打开存储数据的原始文件data.dat
FILE *pf = fopen("data.dat", "rb");
if (pf == nullptr)
return 0;
// 这里由于原始数据量缩小,所以这里文件划分的个数也变小了,11个小文件
const int FILE_NO = 11;
FILE *pfile[FILE_NO] = { nullptr };
for (int i = 0; i < FILE_NO; ++i)
{
char filename[20];
sprintf(filename, "data%d.dat", i + 1);
pfile[i] = fopen(filename, "wb+");
}
// 哈希映射,把大文件中的数据,映射到各个小文件当中
int data;
while (fread(&data, 4, 1, pf) > 0)
{
int findex = data % FILE_NO;
fwrite(&data, 4, 1, pfile[findex]);
}
// 定义一个链式哈希表
unordered_map<int, int> numMap;
// 先定义一个小根堆
using P = pair<int, int>;
using FUNC = function<bool(P&, P&)>;
using MinHeap = priority_queue<P, vector<P>, FUNC>;
MinHeap minheap([](auto &a, auto &b)->bool {
return a.second > b.second; // 自定义小根堆元素大小比较方式
});
// 分段求解小文件的top 10大的数字,并求出最终结果
for (int i = 0; i < FILE_NO; ++i)
{
// 恢复小文件的文件指针到起始位置
fseek(pfile[i], 0, SEEK_SET);
// 这里直接统计了数字重复的次数
while (fread(&data, 4, 1, pfile[i]) > 0)
{
numMap[data]++;
}
int k = 0;
auto it = numMap.begin();
// 如果堆是空的,先往堆放10个数据
if (minheap.empty())
{
// 先从map表中读10个数据到小根堆中,建立top 10的小根堆,最小的元素在堆顶
for (; it != numMap.end() && k < 10; ++it, ++k)
{
minheap.push(*it);
}
}
// 把K+1到末尾的元素进行遍历,和堆顶元素比较
for (; it != numMap.end(); ++it)
{
// 如果map表中当前元素重复次数大于,堆顶元素的重复次数,则替换
if (it->second > minheap.top().second)
{
minheap.pop();
minheap.push(*it);
}
}
// 清空哈希表,进行下一个小文件的数据统计
numMap.clear();
}
// 堆中剩下的就是重复次数最大的前k个
while (!minheap.empty())
{
auto &pair = minheap.top();
cout << pair.first << " : " << pair.second << endl;
minheap.pop();
}
return 0;
}
leetcode相关题目
最小的k个数
输入整数数组 arr ,找出其中最小的 k 个数。例如,输入4、5、1、6、2、7、3、8这8个数字,则最小的4个数字是1、2、3、4。
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
输入:arr = [0,1,2,1], k = 1
输出:[0]
我的思路1:
- 大根堆:要找最小的前k个,维护一个大根堆,里面存前k个数字,然后遍历数组,比堆顶小的,换入
class Solution {
public:
//要找最小的前k个,维护一个大根堆,里面存前k个数字,然后遍历数组,比堆顶小的,换入
vector<int> getLeastNumbers(vector<int>& arr, int k)
{
if(k <= 0) return vector<int>();
//存前k个数字
priority_queue<int> pq; //优先级队列默认由大到小排列
int i = 0;
while(i < k)
{
pq.push(arr[i]);
i++;
}
//遍历数组,比堆顶小的,换入
int size = arr.size();
while(i < size)
{
if(arr[i] < pq.top())
{
pq.pop();
pq.push(arr[i]);
}
i++;
}
//将优先级队列导入vector
vector<int> rt;
while(!pq.empty())
{
rt.push_back(pq.top());
pq.pop();
}
return rt;
}
};
我的思路2:
- 使用快排分割函数
- 要找最小的前k个,使用快排分割,每次用一个基准进行一次快排,一次快排过后,基准左边都是比基准小的,右边都是大的
- 然后看基准的下标是不是k-1,是的话,结束,不是的话看基准位置比k大还是比k小,
- 比k小那么下次在右部分再进行一次快排,比k大下次在左部分继续快排分割
class Solution {
public:
//要找最小的前k个,使用快排分割,每次用一个基准进行一次快排,一次快排过后,基准左边都是比基准小的,右边都是大的
//然后看基准的下标是不是k-1,是的话,结束,不是的话看基准位置比k大还是比k小,
//比k小那么下次在右部分再进行一次快排,比k大下次在左部分继续快排分割
int partation(vector<int> & arr, int low, int high, int k)//快排分割函数
{
int base = arr[low]; // 选取基准
while(low < high)
{
while(low < high && arr[high] >= base)
{
high--;
}
if(low < high)
{
arr[low++] = arr[high];
}
while(low < high && arr[low] < base)
{
low++;
}
if(low < high)
{
arr[high--] = arr[low];
}
}
arr[low] = base;
return low;
}
//找到划分后基准位置刚好是k的
int selectK(vector<int> &arr, int start, int end, int k)
{
int pos = partation(arr, start, end, k);
if(pos+1 < k)
{
return selectK(arr, pos+1, end, k);
}
else if(pos+1 > k)
{
return selectK(arr, start, pos, k);
}
else
{
return pos;
}
}
vector<int> getLeastNumbers(vector<int>& arr, int k)
{
if(k<=0) return vector<int>();
selectK(arr, 0, arr.size()-1, k);
//现在数组的前k个就是最小的
arr.resize(k);
return arr;
}
};
版权声明:本文为lsz20000813原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。