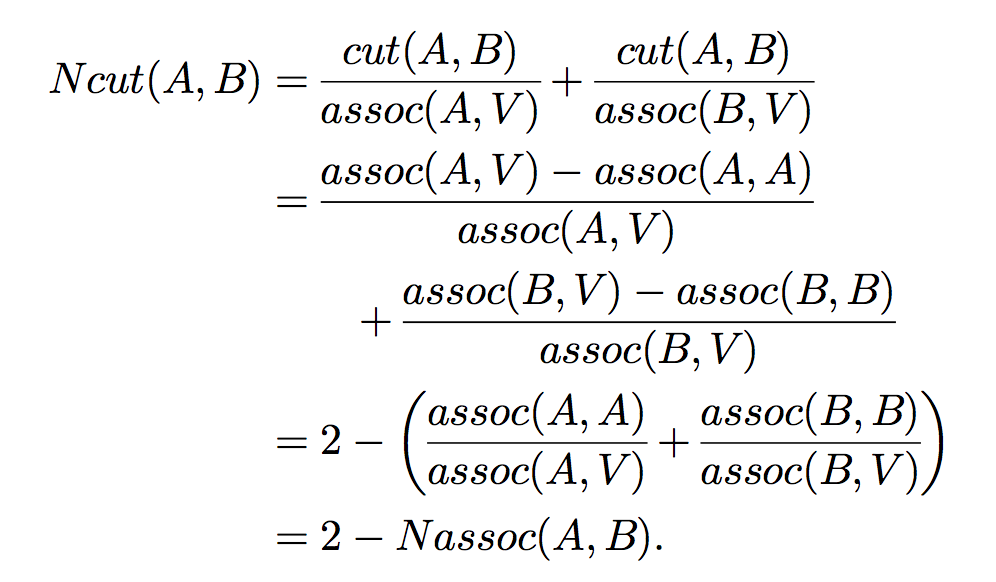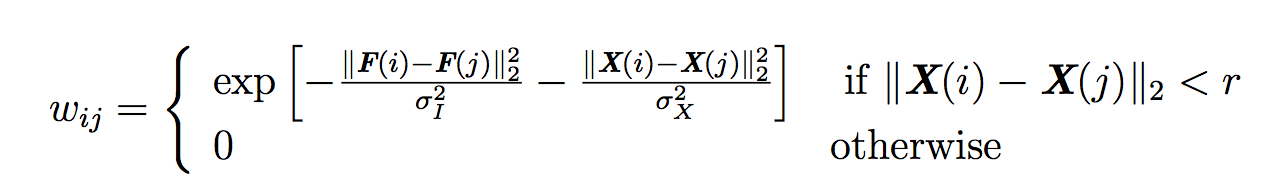归一化切割Normalized cut 是一种分群(cluster grouping)技术,在数据处理和图像处理方面有很广的运用
用其实现图像分割的思路是,把一个图片看成一个图(graph), 然后计算权重图(weighted graph),然后分割成一些具有相同特征(纹理, 颜色,明度等)的区域。
想要理解代码的含义,首先要先要理解一些基本的概念:
1.什么是图(graph)?
我们定义
G
= (
V, E
), 其中,V是顶点(vertex), E是边(edge)。
2.什么是权重图(weighted graph)
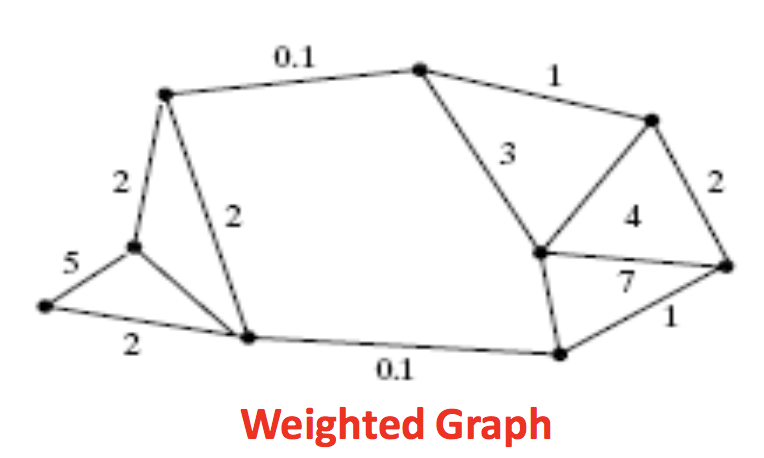
就是边(edge)上有权重(weight)的图,如下图所示:
(图1)
我们把这个图分成两个子集左侧的A和右侧的B, 通过观察,A由4个顶点组成,B由5个顶点组成。需要注意的是,同属于一个子集中的顶点之间的边的权重的值相对来说会大一些。子集与子集直接的点的边上的权重会小, 这个特性也就是normalized cut能分割区域的基础了。这张图表示是,相近的点之间的权重大。但是实际运用中,距离并不是衡量权重的唯一标准。如何计算权重是具体项目具体设计的了。
想要理解normalized cut 需要先理解什么是分割(cut)与最小化分割(min cut)
我这里用相对数学一点的表述方式:
把G = (V,E) 分成两个子集A,B,另:
其中,
就是权重(weight), 最小化分割就是让上式的值最小的分割。如何理解这个过程?
拿图一做例子,我们把图一看成一个整体G,目的是把它分成两个部分。显然中间的两条权重为0.1的边就是最小化切割。最小化分割很完美的就解决了把这个G分成两部分的任务,但是问题来了如下图(图2)所示,最小化切割性能就不很好了。
(图2)
可以看到,图2所示的情况,想要的结果是中间虚线表示的分割,但是最小化切割却切掉了最边缘的角。这很容易理解,因为最小化切割就是让cut(A,B)的值最小的情况,而边缘处cut值确实是最小。因此我们称最小化切割时有偏差的(bias)。如何去除这种偏差就要引入我们这篇文章的主角归一化切割了。
其中:
assoc(A,V)的含义是A中所有点到图中做有点的权重的和。通过上面的公式我们可以很清晰的看到
Ncut在追求不同子集间点的权重最小值的同时也追求同一子集间点的权重最大值
至此,数学含义已经讲的差不多了,但是如果想要写成代码,我们需要用矩阵数学的知识重新把normalized cut解释一遍。
受限我们要定义几个概念:
1)
x
表示一个 N=|V|维的指标向量,
x_i
= 1 如果i顶点在子集A中,
x_i
= -1 如果顶点i在子集B中
2)
, d(i) 的含义就是第i个顶点与其他所有顶点的边的权重之和。
3)设
D
是一个[N,N]维的对角矩阵,d(i) (i从1到N)为对角线元素
4)设
W
是一个[N,N]维的对称矩阵,
W
(i,j) =
,所以
W
就是用来描述点与点之间边的权重的矩阵
5)需要声明的是,在矩阵运算中
1
表示[N,1]维度的全一矩阵
通过种种计算(推导过程参考https://people.eecs.berkeley.edu/~malik/papers/SM-ncut.pdf论文原文pdf文件第三页)[1]
我们的任务就是求解一下特征值问题:
其中y就是特征向量,lambda就是特征值了。我们要的分割点就是
第二小特征值
所对应的特征向量。
计算这个特征值问题的复杂度是
, 不过scipy.sparse.linalg.eig()函数所用的Lanczos算法会将复杂度降到O(n)(毕竟D-W是个稀疏矩阵)
为了利用稀疏矩阵我们需要构建:
,
例子:
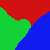
分割图3所示图片,50px X 50px
(图3)
这张彩色RGB图片,我们想要分割,首先设每一个图片中的像素点都是图(graph)中的一个顶点(vertex),然后计算每个点与点之间的权重:
其中
X(i)
表示顶点i在图片中的坐标,
X
是一个[N,1,2]的矩阵,在3维存储着像素点的纵横坐标值。对于灰度图来说F(i)就是i点所在的明度值,F是一个[N,1]的矩阵,对于RGB图片来说F(i) = [B,G,R], F是一个[N,1,3]的矩阵,在3维存着RGB的值。
我们看一下结果:
1)直接求特征值:耗时3分钟
2) 利用
Lanczos方法求稀疏矩阵的特征值耗时3秒
虽然看起来怪怪的,但是后续很容易就能提取出来了(加上滤波二值化之类的等等)。
我这里只是做了二分,想要将图片分成很多部分,需要对剩下的部分迭代几次,这一部分就很简单了。
下面是我写的代码,,大家参考一下。
'''
reference:
[1] J. Shi and J. Malik, “Normalized cuts and image segmentation”,
IEEE Trans. on Pattern Analysisand Machine Intelligence, Vol 22
[2] https://github.com/SatyabratSrikumar/Normalized-Cuts-and-Image-Segmentation-Matlab-Implementation
edited by JY Wang @ 2018-6-3 SYR Unv
'''
import cv2
import numpy as np
from scipy.linalg.decomp import eig
from scipy import sparse
from scipy.sparse.linalg import eigs
class Ncut(object):
'''
This class is write for RGB image, so if you want to processing grayscale, some adjustment should worked on
F_maker, W_maker function :)
'''
def __init__(self, img):
'''
:param img: better no larger than 300px,300px
'''
self.no_rows, self.no_cols, self.channel = img.shape
self.N = self.no_rows * self.no_cols
self.V_nodes = self.V_node_maker(img)
self.X = self.X_maker()
self.F = self.F_maker(img)
# parameter for W clculate
self.r = 2
self.sigma_I = 4
self.sigma_X = 6
# Dense W,D
self.W = self.W_maker()
self.D = self.D_maker()
# V_nodes shape : [self.N,1,3]
def V_node_maker(self, img):
b,g,r = cv2.split(img)
b = b.flatten()
g = g.flatten()
r = r.flatten()
V_nodes = np.vstack((b,g))
V_nodes = np.vstack((V_nodes,r))
return V_nodes
def X_maker(self):
X_temp = np.arange(self.N)
X_temp = X_temp.reshape((self.no_rows,self.no_cols))
X_temp_rows = X_temp // self.no_rows
X_temp_cols = (X_temp // self.no_cols).T
X = np.zeros((self.N, 1, 2))
X[:,:,0] = X_temp_rows.reshape(self.N,1)
X[:,:,1] = X_temp_cols.reshape(self.N,1)
return X
def F_maker(self,img):
if self.channel < 2:
return self.gray_feature_maker(img)
else:
return self.color_img_feature_maker(img)
def gray_feature_maker(self,img):
print('need to ')
def color_img_feature_maker(self,img):
F = img.flatten().reshape((self.N,1,self.channel))
F = F.astype('uint8')
return F
def W_maker(self):
X = self.X.repeat(self.N,axis = 1)
X_T = self.X.reshape((1,self.N,2)).repeat(self.N,axis = 0)
diff_X = X - X_T
diff_X = diff_X[:,:,0]**2 + diff_X[:,:,1]**2
F = self.F.repeat(self.N,axis = 1)
F_T = self.F.reshape((1,self.N,3)).repeat(self.N,axis = 0)
diff_F = F - F_T
diff_F = diff_F[:,:,0]**2 + diff_F[:,:,1]**2 + diff_F[:,:,2]**2
W_map = diff_X < self.r**2 # valid map for W
W = np.exp(-((diff_F / (self.sigma_I**2)) + (diff_X / (self.sigma_X**2))))
return W * W_map
def D_maker(self):
# D is a diagonal matrix using di as diagonal, di is the sum of weight of node i with all other nodes
d_i = np.sum(self.W, axis=1)
D = np.diag(d_i)
return D
def EigenSolver(self):
L = self.D - self.W
R = self.D
lam,y = eig(L, R)
index = np.argsort(lam)
top2 = lam[index[:2]].real
smallest_2 = y[:,index[1]]
print('dense eigenvector')
return smallest_2.real
def EigenSolver_sparse(self):
s_D = sparse.csr_matrix(self.D)
s_W = sparse.csr_matrix(self.W)
s_D_nhalf = np.sqrt(s_D).power(-1)
L = s_D_nhalf @ (s_D - s_W) @ s_D_nhalf
lam,y = eigs(L)
index = np.argsort(lam)
top2 = lam[index[:2]].real
smallest_2 = y[:, index[1]]
print('sparse eigenvector')
return smallest_2.real
if __name__ == '__main__':
# This is dense eigenvector method
# img = cv2.imread('picture/Ncut_test.png', cv2.IMREAD_COLOR)
# cutter = Ncut(img)
# eigenvector = cutter.EigenSolver()
# the process is cost too much time, so I saved the results in a txt file, just ignore this part if you need't
# file = open('result.txt','w')
# for i in eigenvector:
# file.write(str(i))
# file.write(',')
# file = open('result.txt', 'r')
# a = file.read()
# b = np.array(a.split(','))
# This is sparse eigenvector method
img = cv2.imread('picture/Ncut_test.png', cv2.IMREAD_COLOR)
cutter = Ncut(img)
eigenvector = cutter.EigenSolver_sparse()
b = eigenvector
b = b.reshape((50,50)).astype('float64')
b = (b/b.max())*255
cv2.imshow('eigvec',b.astype('uint8'))
cv2.waitKey()
print('Finished!')
参考文献:
[1]
J. Shi and J. Malik, “Normalized cuts and image segmentation”, IEEE Trans. on Pattern Analysisand Machine Intelligence, Vol 22, No. 8, Aug., 2000.
[2]
Jitendra Malik, Jianbo Shi UC Berkeley,
Normalized-Cuts-and-Image-Segmentation
github地址
[3]
Haining Wang,
ECS 231 Final Project,
Image Segmentation by Normalized Cut,
University of California, Davis
转发请标明出处