博客

202112-2-序列查询新解

问题

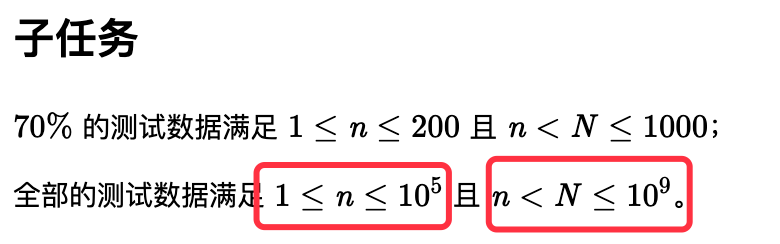
思路

按202112-1-序列查询分段思想，

遍历序列A：

• f(i)分段，隔段f(i)+1
• g(i)分段，隔段g(i)+1

实现

思路1：直接遍历所有i，规模N到10的九次方

n, N = map(int, input().strip().split()) # n, N两个正整数
A = [0] + list(map(int, input().strip().split())) # [0] + A[1]..A[n]
r = N // (n + 1)
G = [i//r for i in range(0, N)]
res = 0 # error(A)
x = 0
for i in range(1, N):
    if i in A:
	    x += 1
    res += abs(G[i] - x)
print(res)

思路2：按n分段，规模n到10的五次方

n, N = map(int, input().strip().split()) # n, N两个正整数
A = [0] + list(map(int, input().strip().split())) # [0] + A[1]..A[n]

r = N // (n + 1)
f_num = [0] * (n+1) # 当前f分段的剩余数的个数
for i in range(n):
	f_num[i] = A[i+1] - A[i]
f_num[n] = N - A[n]

f = g = 0 # f(i),g(i)的初始值
res = 0	# error(A)
g_num = r # 当前g分段的剩余数的个数
while f <= n:
	# 当前f分段的剩余数的个数 >= 当前g分段的剩余数的个数
	if f_num[f] >= g_num: 
		res += abs(g - f) * g_num
		f_num[f] -= g_num
		g += 1
		g_num = r
	# 当前f分段的剩余数的个数 < 当前g分段的剩余数的个数
	else:
		res += abs(g - f) * f_num[f]
		g_num -= f_num[f]
		f += 1
print(res)

• 序列处理类型
  • 总结，注意看题目的数值范围，N为10的九次方规模，512MB内存限制，普通遍历必然超时，就需要
    
    找数字规律了
    
    ，采用了分段的思想