博客

64. 最小路径和

   

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

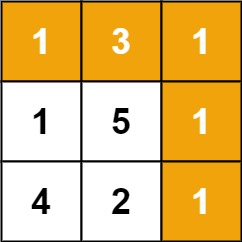
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

思路：参考 LeetCode题解（没有题解自己做，写成了回溯法，遍历所有可能 = =，答案还是错的 哎~）

搜索的做法仅仅在数据规模比较小的时候才考虑使用，因为复杂度较高，所以采用dp。由于每个元素对应的最小路径和与其相邻元素（当前点的上面或左面）对应的最小路径和有关，因此可以使用动态规划求解。

动态规划：从左上角(0, 0)移动到右下角，每次选择最小的节点值移动：

(1) 位于原点(0,0)时，不做任何处理

(2) 当前点位于最上面一行（上边界x=0）时：只能从原点向右移动，从”左”边过来

(3) 当前点位于最左边一列（左边界y=0）时：只能从原点向下移动，从”上”边过来

(4) 当前点既不在最上面一行(i != 0)，也不在最左边一列(j != 0)，此时选取其上或其左位置点的最小值

时间复杂度：O(mn) 遍历整个 grid 矩阵元素

空间复杂度：O(1) 直接修改原矩阵，不使用额外空间

Go版：

// 动态规划1 空间复杂度O(n)
// func minPathSum(grid [][]int) int {
//     m, n := len(grid), len(grid[0])
//     dp := make([][]int, m)
//     for i := 0; i < m; i++ {
//         dp[i] = make([]int, n)
//     }

//     for i := 0; i < m; i++ {
//         for j := 0; j < n; j++ {
//             if i == 0 && j == 0 {
//                 dp[i][j] = grid[i][j]
//             } else if i == 0 {  // 第一行：从左到右
//                 dp[i][j] = dp[i][j-1] + grid[i][j]
//             } else if j == 0 {  // 第一列：从上到右
//                 dp[i][j] = dp[i - 1][j] + grid[i][j]
//             } else {
//                 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
//             }
//         }
//     }

//     return dp[m - 1][n - 1]
// }

// 动态规划2 空间复杂度O(1) 原地修改
func minPathSum(grid [][]int) int {
    m, n := len(grid), len(grid[0])

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if i == 0 && j == 0 {
                continue
            } else if i == 0 {  // 第一行：从左到右
                grid[i][j] = grid[i][j-1] + grid[i][j]
            } else if j == 0 {  // 第一列：从上到下
                grid[i][j] = grid[i - 1][j] + grid[i][j]
            } else {
                grid[i][j] = min(grid[i-1][j], grid[i][j-1]) + grid[i][j]
            }
        }
    }

    return grid[m - 1][n - 1]
}

/**************************************************************************/
// 参考：https://leetcode.cn/problems/minimum-path-sum/solutions/1159882/dong-tai-gui-hua-di-gui-bei-wang-lu-di-g-q5uo/
// 递归（超时，要加上记忆化搜索）
// var m, n int
// func minPathSum(grid [][]int) int {
//     m, n = len(grid), len(grid[0])

//     return dfs(grid, 0, 0) // 出发点本身的值也算上
// }

// // 每次只能向下或者向右移动一步
// func dfs(grid [][]int, i, j int) int {
//     // 递归终止条件
//     if i >= m || j >= n {
//         return math.MaxInt32
//     }

//     // 拼凑结果
//     if i == m - 1 && j == n - 1 {
//         // fmt.Println("***", grid[i][j])
//         return grid[i][j]
//     }

//     // 下探到下一层
//     return min(dfs(grid, i, j + 1), dfs(grid, i + 1, j)) + grid[i][j] 
 
// }

/**************************************************************************/
// 递归 + 记忆化搜索
// var m, n, flag int
// var dp [][]int
// func minPathSum(grid [][]int) int {
//     m, n = len(grid), len(grid[0])

//     dp = make([][]int, m)
//     for i := 0; i < m; i++ {
//         dp[i] = make([]int, n)
//     }

//     flag = -1 // 标记当前格子是否遍历过
//     for i := 0; i < m; i++ {
//       for j := 0; j < n; j++ {
//          dp[i][j] = flag
//       }
//    }

//     res := dfs(grid, 0, 0) // 出发点本身的值也算上
//     fmt.Println("... ", dp)
//     return res
// }

// // 每次只能向下或者向右移动一步
// func dfs(grid [][]int, i, j int) int {
//     // 递归终止条件
//     if i >= m || j >= n {
//         return math.MaxInt32
//     }

//     // 拼凑结果
//     if i == m - 1 && j == n - 1 {
//         // fmt.Println("***", grid[i][j])
//         return grid[i][j] // 为什么这里要返回grid[i][j] ???
//     }

//     // 下探到下一层
//     if dp[i][j] == flag {
//         dp[i][j] = min(dfs(grid, i, j + 1), dfs(grid, i + 1, j)) + grid[i][j]
//     }
    
//     // fmt.Println("***", dp[i][j])
//     return dp[i][j]
// }

func min(nums ...int) int {
    minVal := nums[0]
    for _, num := range nums {
        if num < minVal {
            minVal = num
        }
    }

    return minVal
}

C++版：

// dp:
int minPathSum(vector<vector<int>>& grid) {
    for (int i = 0; i < grid.size(); i++)
    {
        for (int j = 0; j < grid[0].size(); j++)
        {
            if (i == 0 && j == 0) // (1) 位于原点(0,0)时
            {
                continue;
            }
            else if (i == 0)      // (2) 当前点位于最上面一行（上边界x=0）时：只能从原点向右移动，从"左"边过来
            {
                grid[i][j] = grid[i][j - 1] + grid[i][j]; 
            }
            else if (j == 0)      // (3) 当前点位于最左边一列（左边界y=0）时：只能从原点向下移动，从"上"边过来
            {
                grid[i][j] = grid[i - 1][j] + grid[i][j];
            }
            else                  // (4) 当前点既不在最上面一行(i != 0)，也不在最左边一列(j != 0)，此时选取其上或其左位置点的最小值
            {
                grid[i][j] = min(grid[i - 1][j]/*上面位置*/, grid[i][j - 1]/*左面位置*/) + grid[i][j];
            }
        }
    }
    return grid[grid.size() - 1][grid[0].size() - 1];    // 最终返回右下角的累计的最小路径和
}