博客

1.图的存储

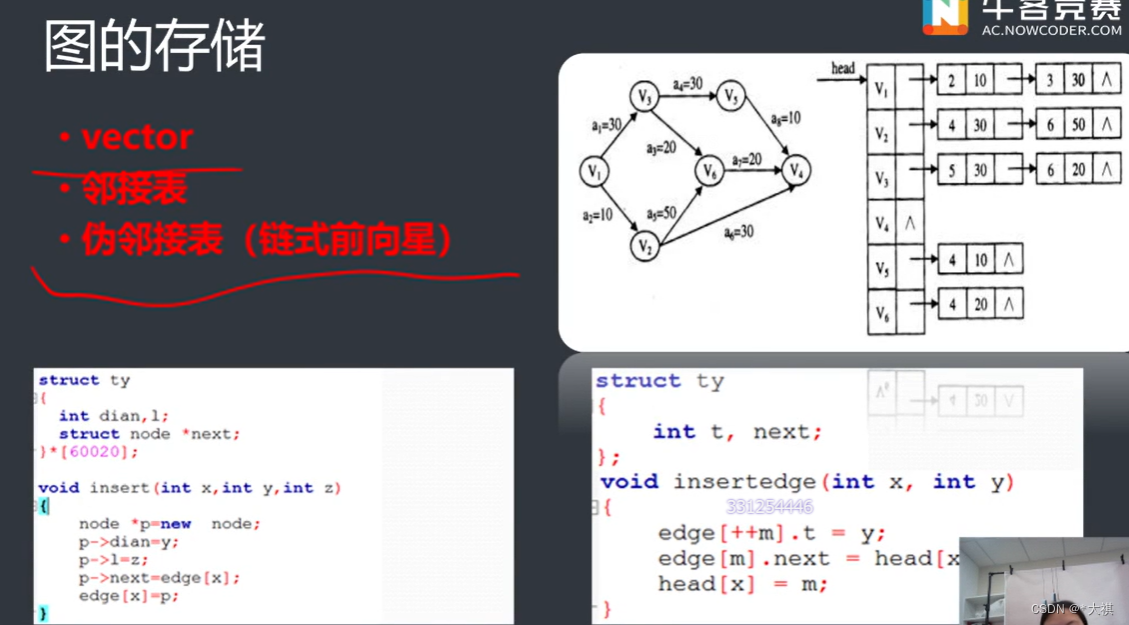
图的BFS遍历

2.欧拉图

（即能不重复得走完所有边且


起点和终点相同


的为欧拉图，只能不重复走完所有边但不能回到起点的是半欧拉图）

3.拓扑排序

1）概念引入

一个工程常被分为多个小的子工程，这些子工程被称为活动（Activity），在有向图中若以顶点表示活动，有向边表示活动之间的先后关系，这样的·图简称为AOV网。在AOV网中为了更好地完成工程，必须满足活动之间先后关系，需要将各活动排一个先后次序即为拓扑排序。

（其实这个在我们生活中很常见啦，比如学校要排一个课表，规定必须要先上完高数再上线性代数，要先上完C语言再上数据结构……）

2）解法

只要每次去找入度为0的点（符合执行条件），取出它作为答案并将其删除，同时删除它到其它顶点的边，再重复此过程，直到顶点全部删完或是没有办法删除结点了（存在环，无解）

可以看出拓扑排序是有多解的

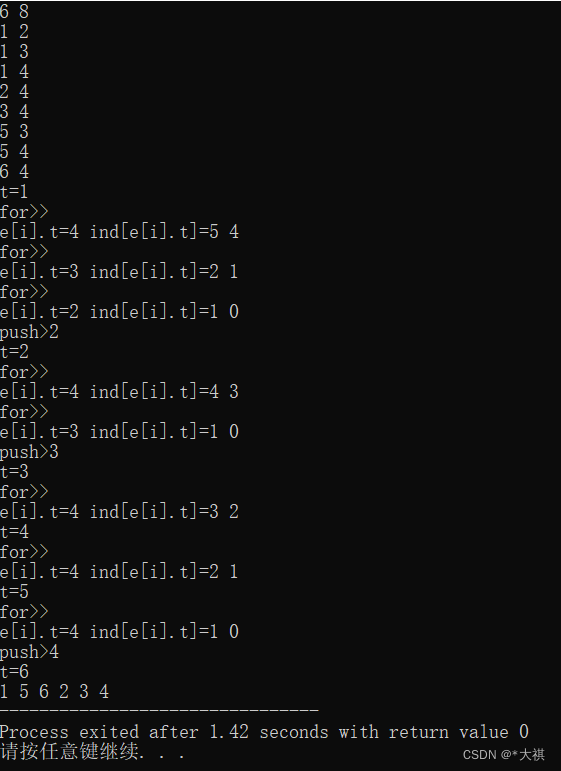
3）代码

#include<iostream>
#include<queue>
using namespace std;
const int M=1e6+6;
int n,m,head[M],ct,ind[M],ans[M];
queue<int> q;
struct ED{
	int t,next;
}e[M];
void addedge(int u,int v){
	e[++ct].t=v;
	e[ct].next=head[u];
	head[u]=ct;
}
void tuopu(){
	int t=0;
	for(int i=1;i<=n;i++){
		if(!ind[i])q.push(i);
	}
	while(!q.empty()){
		int x=q.front();
		ans[t++]=x;
		//cout <<"t="<<t<<'\n';
		q.pop();
		for(int i=head[x];i!=-1;i=e[i].next){
			//cout <<"for>>\n";
			//cout <<"e[i].t="<<e[i].t<<' '<<"ind[e[i].t]="<<ind[e[i].t]<<' ';
			ind[e[i].t]--;
			//cout <<ind[e[i].t]<<'\n';
			if(!ind[e[i].t]){
				q.push(e[i].t);
				//cout <<"push>"<<e[i].t<<'\n';
			}
		}
	}
	if(t!=n)cout <<-1;
	else
		for(int i=0;i<n;i++)cout <<ans[i]<<' ';
}
int main(){
	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)head[i]=-1;
	int x,y;
	for(int i=0;i<m;i++){
		cin >>x>>y;
		addedge(x,y);
		ind[y]++;
	}
	tuopu(); 
	return 0;
}
/*
6 8
1 2
1 3
1 4
2 4
3 4
5 3
5 4
6 4
*/
//因为每个点每条边都只访问了一次所以复杂度是O(n+m) 

为了便于理解其过程，把中间变量打印了一些

AOE网 关键路径

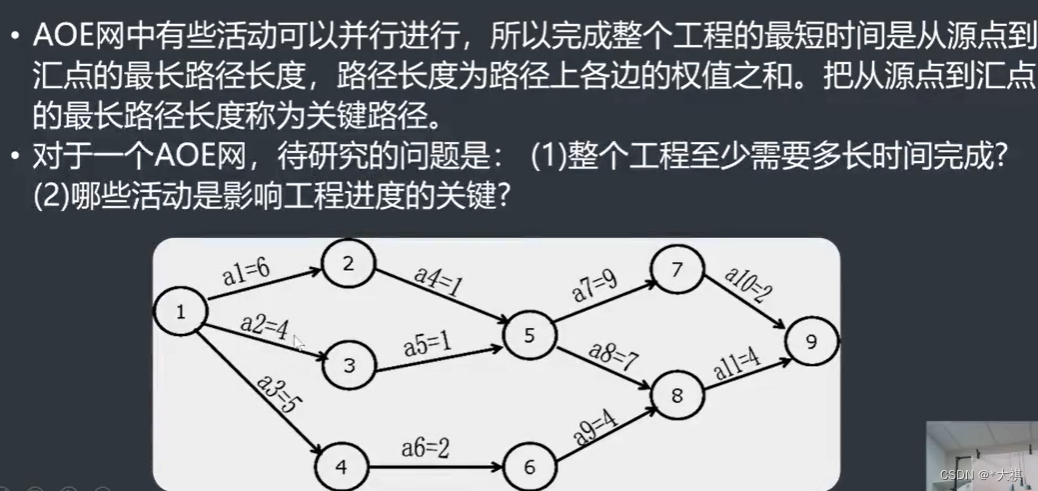
做法：从左往右按照拓扑的方法求出每个结点的最早开始时间，再从右往左，逆推出每个结点开始的最晚时间，如果最早时间==最晚时间，就是关键的路径上的点。