1.边界值分析
基本原理:错误更可能出现在输入变量的极值附近。
基本思想:使用在最小值、略高于最小值、正常值、略低于最大值和最大值处取输入变量值。
工具:T,可以为恰当描述的程序生成这类测试用例,该工具将上述值叫做min,min+,nom,max-和max。
关键假设:“单缺陷”假设,失效极少是由于两个(多个)缺陷的同时发生引起的,因此边界值分析测试用例的获得,通过使所有变量取正常值,只使一个变量取极值。
归纳边界值分析:如果一个n变量函数,使除一个以外的所有变量取正常值,使剩余的那个变量取min,min+,nom,max-,max,对每个变量都重复进行这样,对于一个n变量函数,边界值分析会产生多少个测试用例呢?
2.边界值分析的局限性
如果被测程序是多个独立变量的函数,这些变量受物理量的限制,则很适合边界值分析
3.健壮性测试
是边界值分析的一个简单扩展,除了变量的五个边界值分析取值,还要通过采用一个略超过最大值(max+)的取值,以及一个略小于最小值(min-)的取值,看看超过极值时系统会有什么表现。
健壮性测试的主要价值是观察例外处理情况。
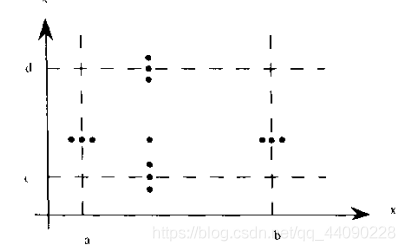
4.最坏情况测试:
边界值测试分析采用了可靠性理论的单缺陷假设,如果拒绝这种假设。对每个变量,首先进行包含min,min+,nom,max-,max的测试,然后对于这些集合进行笛卡尔积,生成测试用例。
这种方法显然更彻底,因为边界值分析测试用例是该方法测试用例的真子集。
边界值测试、健壮性测试(单缺陷)、最坏情况测试、健壮最坏情况测试(多缺陷)产生测试用例个数依次是
4
n
+
1
,
6
n
+
1
,
5
n
,
7
n
4n+1,6n+1,5^n,7^n
4
n
+
1
,
6
n
+
1
,
5
n
,
7
n
。了解更多详情见:
https://blog.csdn.net/qq_33208851/article/details/105901860