博客

OMPL库教程翻译/OMPL学习

  • Post author:
  • Post category:其他


本文翻译自OMPL教程，以备自己查阅。不准确之处欢迎在评论区提意见。


前言

一、简介


The Open Motion Planning Library(OMPL)

是基于采样方法的开源运动规划库，其规划算法可以分为两类：


  • Geometric planners


  • Control-based planners


特性：

基于采样，概率完备，非最优/渐进最优


morse仿真环境下使用ompl

二、

规划算法汇总

2.1 Geometric planners


How OMPL selects a geometric planner:

If you use the

ompl::geometric::SimpleSetup

class (highly recommended) to define and solve your motion planning problem, then OMPL will automatically select an appropriate planner (unless you have explicitly specified one). If the state space has a default projection (which is going to be the case if you use any of the built-in state spaces), then it will use

LBKPIECE

if a bidirectional planner can be used and otherwise it will use

KPIECE

. These planners have been shown to work well consistently across many real-world motion planning problems, which is why these planners are the default choice. In case the state space has no default projection,

RRTConnect

or regular

RRT

will be used, depending on whether a bidirectional planner can be used. The notion of a goal is very general in OMPL: it may not even be possible to sample a state that satisfies the goal, in which case OMPL cannot grow a second tree at a goal state.


2.1.1 Multi-query planners

a)

Probabilistic RoadmaMethod (PRM)

b)

SPArse Roadmap Spanner algorithm (SPARS)


c)

SPARS2


2.1.2 Single-query planners

a)

Rapidly-exploring Random Trees (RRT) 非最优

b)

Expansive Space Trees (EST)

c)

Kinematic Planning by Interior-Exterior Cell Exploration (KPIECE)

d)

Search Tree with Resolution Independent Density Estimation (STRIDE)


e)

Path-Directed Subdivision Trees (PDST)


f)

Fast Marching Tree algorithm (FMT∗)


g)

Bidirectional Fast Marching Tree algorithm (BFMT∗)


2.1.3 Optimizing planners

a)

PRM*


b)

LazyPRM*


c)

RRT* 渐进最优


d)

RRT#


e)  RRTX

f)

Informed RRT*


g)

Batch Informed Trees (BIT*)


h)

Lower Bound Tree RRT (LBTRRT)


i)

Sparse Stable RRT(SST)


j)

Transition-based RRT (T-RRT)


k)

SPARS


l)

SPARS2


m)

FMT*


n)

CForest


o)

AnytimePathShortening (APS)

Other tools:

图1 预定义规划算法

2.2 Control-based planners

These planners rely on

state propagation

rather than simple interpolation to generate motions. These planners do not require

a steering function

, but all of them (except KPIECE) will use it if the user implements it.


How OMPL selects a control-based planner:

If you use the

ompl::control::SimpleSetup

class (highly recommended) to define and solve your motion planning problem, then OMPL will automatically select an appropriate planner (unless you have explicitly specified one). If the state space has a default projection (which is going to be the case if you use any of the built-in state spaces), then it will use

KPIECE

. This planner has been shown to work well consistently across many real-world motion planning problems, which is why it is the default choice. In case the state space has no default projection,

RRT

will be used. Note that there are no bidirectional control-based planners, since we do not assume that there is a steering function that can connect two states

exactly

.

a)

Rapidly-exploring Random Trees (RRT)

(kinodynamic adaptation of the corresponding geometric planners above)

b)

Sparse Stable RRT(SST)

(kinodynamic adaptation of the corresponding geometric planners above)

c)

Expansive Space Trees (EST)


d)

Kinodynamic Planning by Interior-Exterior Cell Exploration (KPIECE)


e)

Path-Directed Subdivision Trees (PDST)


f)

Syclop

g)

Linear Temporal Logical Planner (LTLPlanner)

2.3

自定义运动规划器


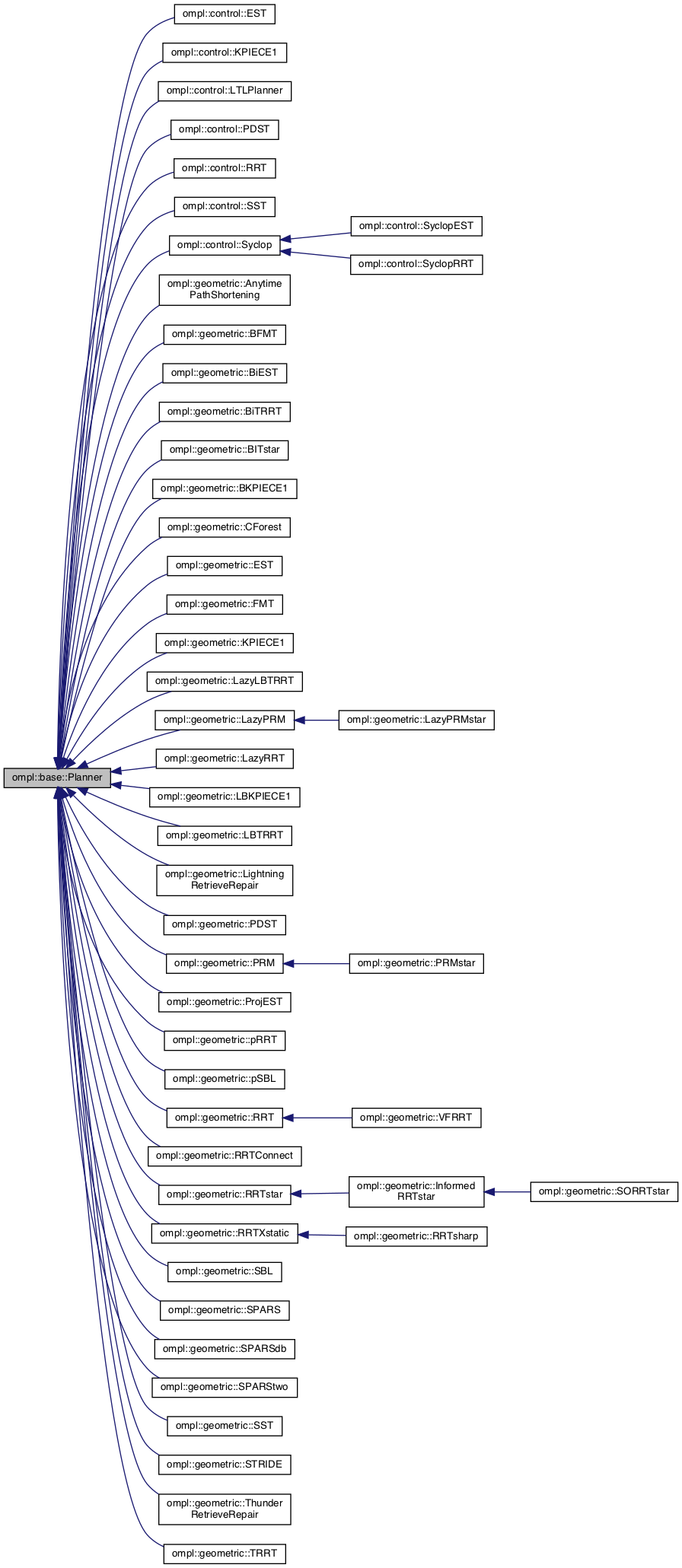
2.3.1 必需项

使用OMPL定义新的运动规划器非常简单，有两个必需满足的条件：

满足以上条件，即可集成进OMPL框架。


2.3.2 可选项

除必需项外，还有其它可以重写的方法，还有其它应沿用的便于集成的经验。这些不是必需的，但是强烈建议使用以实现简明性和一致性：


2.3.3 规划器参数可调

OMPL规划器提供了接口函数

ompl::base::Planner::declareParam()

以定义那些允许用户调节的参数。强烈建议为自定义规划器的所有参数添加此功能。示例可参见

RRTstar.cpp

。需要配置对应的设置函数setter和取值函数函数getter。 

void declareParam(const std::string &name, const PlannerType &planner, const SetterType &setter,
                  const GetterType &getter, const std::string &rangeSuggestion = "")
void declareParam(const std::string &name, const PlannerType &planner, const SetterType &setter,
                  const std::string &rangeSuggestion = "")
Planner::declareParam<double>("range", this, &RRTstar::setRange, &RRTstar::getRange, "0.:1.:10000.");
void setRange(double distance){ maxDistance_ = distance; }
double getRange() const{ return maxDistance_; }


declareParam()

的可选参数rangeSuggestion允许为可调参数给定建议范围。该范围将被OMPL.app GUI用于创建界面插件，用户可通过交互界面修改参数的值。更多关于如何表述建议范围的说明参见

ompl::base::GenericParam::rangeSuggestion_

。

Suggested range for the parameter.

This can be used to provide a hint to, e.g., a GUI. The convention used in OMPL is to denote ranges for the following types as follows:

  • bool: “0,1”
  • enum: “<enum_val0>,<enum_val1>,<enum_val2>,…”
  • int, double: either “first:last” or “first:stepsize:last”. In the first case, the stepsize is assumed to be 1. It is important to use floating point representations for double ranges (i.e., “1.” instead of “1”) to make sure the type is deduced correctly.

Definition at line

131

of file

GenericParam.h

.


2.3.4 自定义规划器示例模板

以下是格式模板，可以被用来创建新的规划器对象： 

#include <ompl/base/Planner.h>
// often useful headers:
#include <ompl/util/RandomNumbers.h>
#include <ompl/tools/config/SelfConfig.h>
namespace ompl
{
    class myNewPlanner : public base::Planner
    {
    public:
        myNewPlanner(const base::SpaceInformationPtr &si) : base::Planner(si, "the planner's name")
        {
            // the specifications of this planner (ompl::base::PlannerSpecs)
            specs_.approximateSolutions = ...;
            specs_.recognizedGoal = ...;
            ...
        }
        virtual ~myNewPlanner(void)
        {
            // free any allocated memory
        }
        virtual base::PlannerStatus solve(const base::PlannerTerminationCondition &ptc)
        {
            // make sure the planner is configured correctly; ompl::base::Planner::checkValidity
            // ensures that there is at least one input state and a ompl::base::Goal object specified
            checkValidity();
            // get a handle to the Goal from the ompl::base::ProblemDefinition member, pdef_
            base::Goal *goal = pdef_->getGoal().get();
            // get input states with PlannerInputStates helper, pis_
            while (const base::State *st = pis_.nextStart())
            {
                // st will contain a start state.  Typically this state will
                // be cloned here and inserted into the Planner's data structure.
            }
            // if needed, sample states from the goal region (and wait until a state is sampled)
            const base::State *st = pis_.nextGoal(ptc);
            // or sample a new goal state only if available:
            const base::State *st = pis_.nextGoal();
            // periodically check if ptc() returns true.
            // if it does, terminate planning.
            while (ptc() == false)
            {
                // Start planning here.
                // call routines from SpaceInformation (si_) as needed. i.e.,
                // si_->allocStateSampler() for sampling,
                // si_->checkMotion(state1, state2) for state validity, etc...
                // use the Goal pointer to evaluate whether a sampled state satisfies the goal requirements
                // use log macros for informative messaging, i.e., logInfo("Planner found a solution!");
            }
            // When a solution path is computed, save it here
            pdef_->addSolutionPath(...);
            // Return a value from the PlannerStatus enumeration.
            // See ompl::base::PlannerStatus for the possible return values
            return base::PlannerStatus::EXACT_SOLUTION;
        }
        virtual void clear(void)
        {
            Planner::clear();
            // clear the data structures here
        }
        // optional, if additional setup/configuration is needed, the setup() method can be implemented
        virtual void setup(void)
        {
            Planner::setup();
            // perhaps attempt some auto-configuration
            SelfConfig sc(si_, getName());
            sc.configure...
        }
        virtual void getPlannerData(base::PlannerData &data) const
        {
            // fill data with the states and edges that were created
            // in the exploration data structure
            // perhaps also fill control::PlannerData
        }
    };
}


2.3.5

为自定义规划器创建python接口


API说明

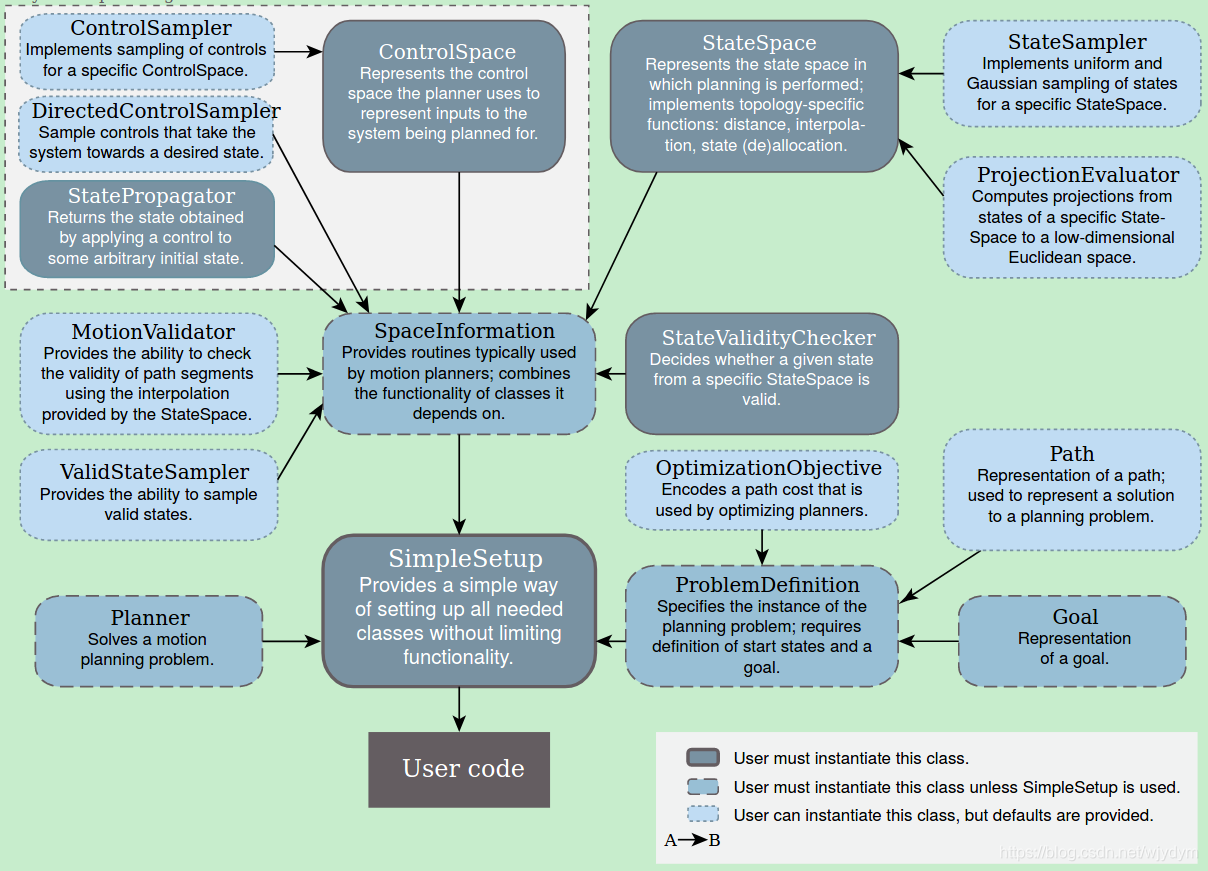
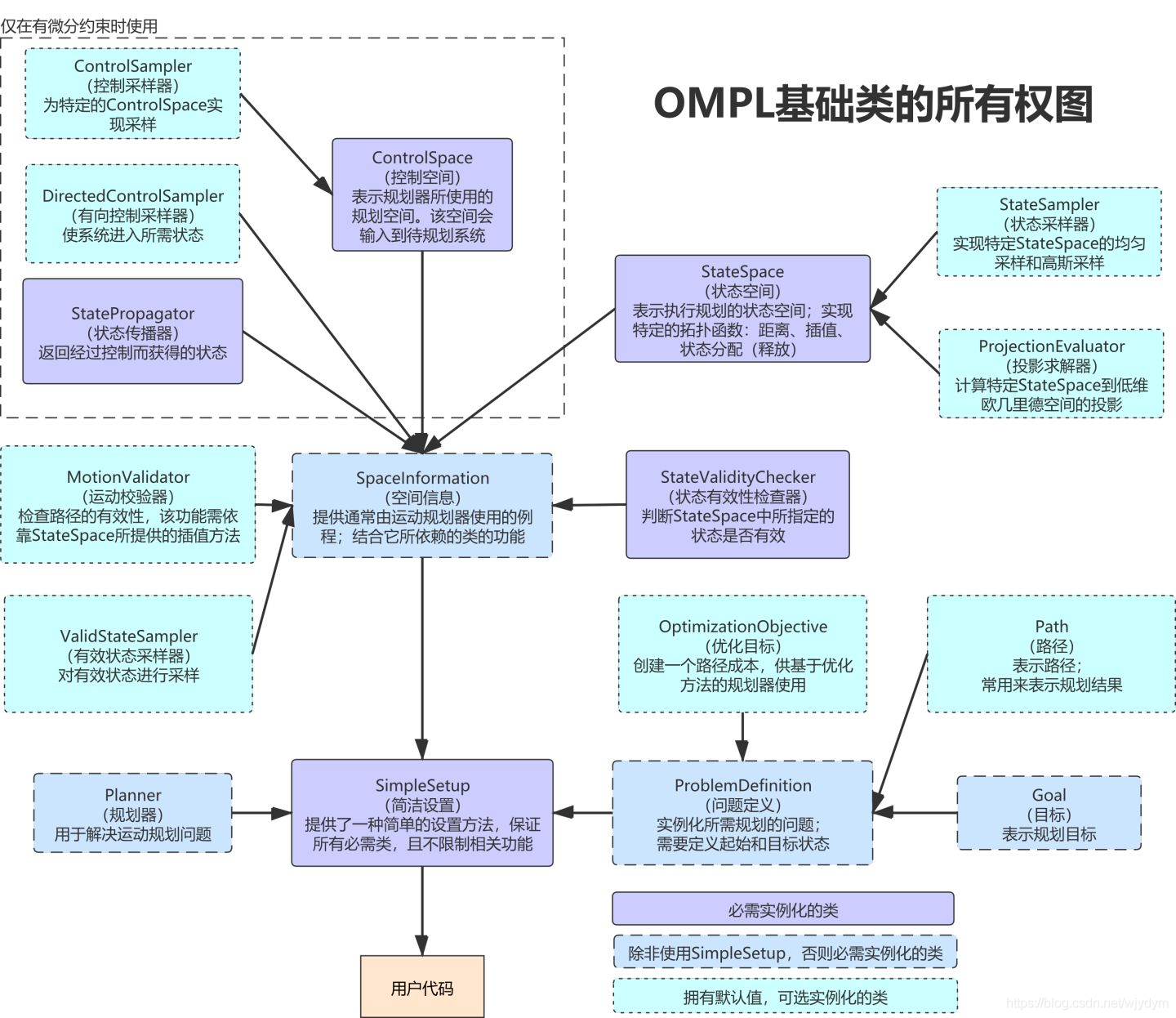
一、概览

http://ompl.kavrakilab.org/api_overview.html


图2 API概览

几个

关键对象

：

状态采样器

，

映射器

，

状态

及

状态空间

(

约束

及

约束状态空间

)，

有效状态采样器

，评估器(

状态

或

运动

)，

空间描述

，

优化对象

，

起始点

，

求解对象

，

规划器

，

简易设置器

。

1.1

一般步骤

（建议

ompl::geometric::SimpleSetup

）

  • identify the space we are planning in: SE(3)
  • select a corresponding state space from the available ones, or implement one. For SE(3), the

    ompl::base::SE3StateSpace

    is appropriate.
  • since SE(3) contains an R3 component, we need to define bounds.
  • define the notion of state validity.
  • define start states and a goal representation.


1.1.1 实例化一个

状态空间

构建一个规划问题的第一步是选择欲进行规划的空间。构建一个自定义空间(继承自

ompl::base::StateSpace

)或预定义空间的实例化对象。如果改变采样方法或距离计算方法的定义，将进一步具化该状态空间。 

namespace ob = ompl::base;
namespace og = ompl::geometric;
// construct the state space we are planning in
ob::StateSpacePtr space(new ob::SE3StateSpace());
// set bounds
ob::RealVectorBounds bounds(3);
bounds.setLow(-1);
bounds.setHigh(1);
space->setBounds(bounds);


1.1.2 实例化一个

控制空间

如果规划问题含有微分约束，那么有必要用到控制空间。构建一个自定义控制空间(继承自

ompl::control::ControlSpace

)的实例化对象。通常

ompl::control::RealVectorControlSpace

已经够用了。 

ob::StateSpacePtr space(new ob::SE3StateSpace());
// set bounds for state space
……
ompl::control::ControlSpacePtr cspace(new control::RealVectorControlSpace(space));
// set bounds for cspace
……


1.1.3 实例化一个

空间信息类

创建一个空间信息类(

ompl::base::SpaceInformation

)的实例化对象较为简单，其构造函数只需要一个状态空间(

ompl::base::StateSpace

)作为传入参数。当使用的是控制空间时，需要使用

ompl::control::SpaceInformation

，其构造函数除状态空间参数外还有控制空间参数

ompl::control::ControlSpace

，并且还需要通过

setStatePropagator()

设置statePropagator_变量(参数可以是一个StatePropagatorPtr，也可以是一个std::function可调用对象，具体情况阅读

源码

就清楚了)。

StatePropagator

可以认为是执行器，将控制转化为状态。

在使用空间信息类之前，还需以下配置：

注：无上下限的状态空间，其度量值为无穷大。 

// define this class:
class myStateValidityCheckerClass : public ob::StateValidityChecker
{
public:
     myStateValidityCheckerClass(const ob::SpaceInformationPtr &si) :
       ob::StateValidityChecker(si)
        {
     }
     virtual bool isValid(const ob::State *state) const
     {
             return ...;
     }
};
// or this function:
bool myStateValidityCheckerFunction(const ob::State *state)
{
     return ...;
}
ob::SpaceInformationPtr si(space);
// either this call:
si->setStateValidityChecker(std::make_shared<myStateValidityCheckerClass>(si));
// or this call:
si->setStateValidityChecker(myStateValidityCheckerFunction);
si->setStateValidityCheckingResolution(0.03); // 3%
si->setup();

注：设置完参数后一定要调用

setup()

将设置载入。


1.1.4 实例化一个

问题描述

 

base::SpaceInformationPtr si(...);
base::ProblemDefinitionPtr pdef(new base::ProblemDefinition(si));
base::ScopedState start;
// fill start state
base::ScopedState goal;
// fill goal state
pdef->setStartAndGoalStates(start, goal);

注：设置起始和终止状态是问题描述非常重要的步骤。


1.1.5 实例化一个

规划器

欲使用运动规划器(

ompl/geometric/planners

中的ompl::geometric::XXX或

ompl/control/planners

中的ompl::control::XXX) ，必须已有一个空间信息实例(

base::SpaceInformation

或

control::SpaceInformation

)，作为规划器构造函数的传入参数。 

using namespace ompl;
base::SpaceInformationPtr si(...);
base::ProblemDefinition   pdef(si);
// set start states & goal region for the problem definition
base::PlannerPtr planner(new geometric::SBL(si));
planner->setProblemDefinition(pdef);
planner->solve(1.0);
if (pdef->getGoal()->getSolutionPath())
{
   // do something with the solution
}
planner->clear();


1.1.6 路径简化器


PathSimplifier

生成的路径结果可使用

ompl::geometric::PathSimplifier


简化

。


简化方法

SimpleSetup

上述实例化操作已简化至

ompl::geometric::SimpleSetup

(

ompl::control::SimpleSetup

)。 


//>>>>>>>>And a state validity checking function defined like this:
bool isStateValid(const ob::State *state)
//>>>>>>>>We first create an instance of the state space we are planning in.
void planWithSimpleSetup()
{
//>>>>>>>>Create an instance of ompl::geometric::SimpleSetup. Instances of ompl::base::SpaceInformation, and ompl::base::ProblemDefinition are created internally.
    og::SimpleSetup ss(space);
//>>>>>>>>Set the state validity checker
    ss.setStateValidityChecker([](const ob::State *state) { return isStateValid(state); });
//>>>>>>>>Create a random start state:
    ob::ScopedState<> start(space);
    start.random();
//>>>>>>>>And a random goal state:
    ob::ScopedState<> goal(space);
    goal.random();
//>>>>>>>>Set these states as start and goal for SimpleSetup.
    ss.setStartAndGoalStates(start, goal);
/*We can now try to solve the problem. This will also trigger a call to 
ompl::geometric::SimpleSetup::setup() and create a default instance of 
a planner, since we have not specified one. Furthermore, 
ompl::base::Planner::setup() is called, which in turn calls 
ompl::base::SpaceInformation::setup(). This chain of calls will lead to 
computation of runtime parameters such as the state validity checking 
resolution. This call returns a value from ompl::base::PlannerStatus 
which describes whether a solution has been found within the specified 
amount of time (in seconds). If this value can be cast to true, a solution 
was found.*/
    ob::PlannerStatus solved = ss.solve(1.0);
//>>>>>>>>If a solution has been found, we can optionally simplify it and the display it
    if (solved)
    {
        std::cout << "Found solution:" << std::endl;
        // print the path to screen
        ss.simplifySolution();
        ss.getSolutionPath().print(std::cout);
    }

1.2 相关列表

1.3 线程安全

所有的static函数、非类成员函数或类的const成员函数均确保了线程安全性，可以放心使用。若在多线程中同时调用类的


非const成员函数


时无线程安全性，须使用

线程锁

。

1.4 内存管理

所有的基类均定义了

shared_ptr

智能指针——类名

Ptr

，通过

ompl/util/ClassForward.h

中定义的OMPL_CLASS_FORWARD宏实现

：
 

 #define OMPL_CLASS_FORWARD(C)                                                                                          \
     class C;                                                                                                           \
     typedef std::shared_ptr<C> C##Ptr

使用该

*Ptr

智能指针可确保程序结束时内存全部释放，无须delete。OMPL库内部部分类使用了C类型指针而非智能

*Ptr

以避免循环依赖(因为循环依赖将阻止内存释放)。

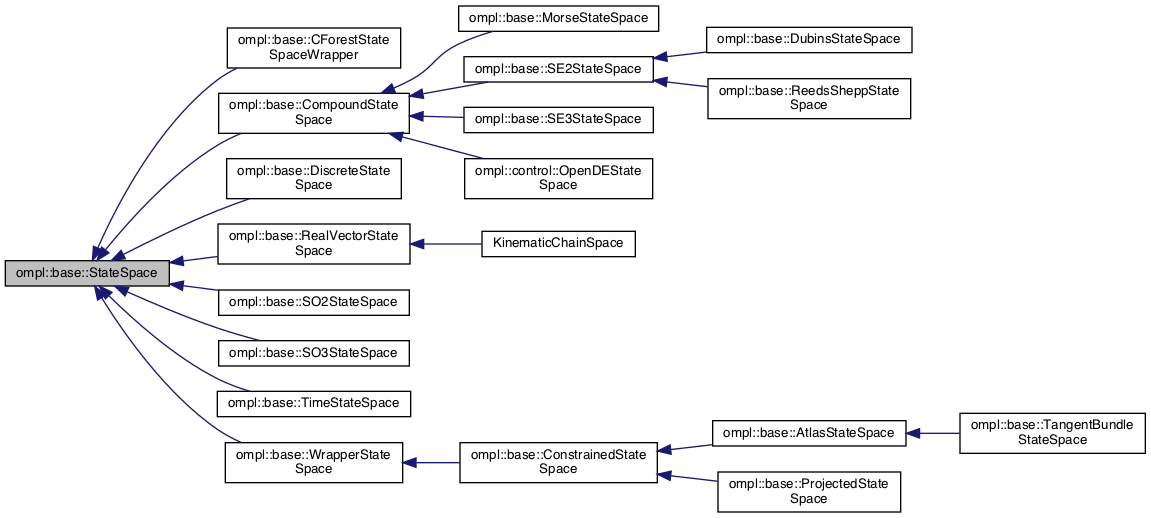
二、

状态及状态空间
图3

预定义状态

图4

预定义状态空间

2.1 合成状态空间

获得新状态空间最简单的方法即合并预定义的状态空间。例如，为获得某机械臂的状态空间，可合并

\mathbb{R}^5

(

ompl::base::RealVectorStateSpace

)和SO2(

ompl::base::SO2StateSpace

)两状态空间，表示5个有运动界限的关节和一个可连续旋转的关节。使用“+”获得的合成状态空间，在计算状态间距时，其各子空间的权重均为1.0。 

ompl::base::StateSpacePtr r5(new ompl::base::RealVectorStateSpace(5));
ompl::base::StateSpacePtr so2(new ompl::base::SO2StateSpace())
ompl::base::StateSpacePtr newSpace = r5 + so2;

如果希望其各子空间的权重不同，应使用

ompl::base::CompoundStateSpace

实例及其

ompl::base::CompoundStateSpace::addSubspace()

函数。 

ompl::base::CompoundStateSpace *newSpace = new ompl::base::CompoundStateSpace();
newSpace->addSubspace(ompl::base::StateSpacePtr(new ompl::base::RealVectorStateSpace(5)), 1.0);
newSpace->addSubspace(ompl::base::StateSpacePtr(new ompl::base::SO2StateSpace()), 0.5);
// put the pointer to the state space in a shared pointer
ompl::base::StateSpacePtr space(newSpace);
// the ompl::base::ScopedState helps only with one cast here, since we still need to
// manually cast the components of the state to what we want them to be.
ompl::base::ScopedState<ompl::base::CompoundStateSpace> state(space);
state->as<ompl::base::SO2StateSpace::StateType>(0)->setIdentity();

2.2 定义状态空间

注：欲验证新定义的状态空间是否满足预期功能性要求时(即确保其合乎状态空间的一系列规则)，可调用

ompl::base::StateSpace::sanityChecks()

。


2.2.1 通过预定义的状态空间自定义状态空间

自定义的状态空间必须继承自

ompl::base::StateSpace

或预定义的状态空间，同时所有的纯虚函数必须给出定义。如果自定义的状态空间使用了新的状态类型，该状态类型必须被命名为

StateType

或通过typedef关键字为其赋予

StateType

别名

。

为使用新定义的状态类型，必须定义

ompl::base::StateSpace::allocState()

和

ompl::base::StateSpace::freeState()

两函数。若定义了新的状态类型，则成员变量

ompl::base::StateSpace::type_

应相应地修改为新的独特值。此外，通常应定义

ompl::base::StateSpace::copyState()

和

ompl::base::StateSpace::equalStates()

两函数。如果状态类型包含实值，可选择地，定义

ompl::base::StateSpace::getValueAddressAtIndex()

函数以分别获取获取这些实值。如果需要序列化或还原序列化，应定义

ompl::base::StateSpace::serialize()

和

ompl::base::StateSpace::deserialize()

函数。


2.2.2 通过合成状态空间自定义状态空间

还可通过继承

ompl::base::CompoundStateSpace

来自定义状态空间，在该自定义状态空间的构造函数中调用

ompl::base::CompoundStateSpace::addSubspace()

函数以引入欲作为子空间的预定义状态空间。这是自定义状态空间的最简便方法，只需要修改构造函数。例如，

ompl::base::SE2StateSpace

。在构造函数中的设置完成后，可选择调用

ompl::base::CompoundStateSpace::lock()

以防止使用者添加子空间。 

SE2StateSpace()
{
    setName("SE2" + getName());
    type_ = STATE_SPACE_SE2;
    addSubspace(std::make_shared<RealVectorStateSpace>(2), 1.0);
    addSubspace(std::make_shared<SO2StateSpace>(), 0.5);
    lock();  //Prevent the user of the state space from adding further components.
}

2.3 映射器

更多关于映射器的介绍见：

Șucan, Ioan A., Kavraki Lydia E., On the Performance of Random Linear Projections for Sampling-Based Motion Planning, in

IEEE/RSJ International Conference on Intelligent Robots and Systems

, pp. 2434-2439, Oct 2009. DOI:

http://dx.doi.org/10.1109/IROS.2009.5354403

.


2.3.1

映射器定义

大部分规划器使用数据结构(如树、图)来引导对状态空间的探测。许多情况下，这种数据结构表现为状态空间的离散形式。但面对高维度的任务空间，这种离散处理并不可行。许多规划算法将状态空间向低维度的欧式空间(如

\mathbb{R}^2

、

\mathbb{R}^3

)映射，再对欧式空间进行离散化处理。比如

ProjEST

，

SBL

，

KPIECE1

等规划算法。这种映射可看做哈希函数。

为适配这种需求，OMPL提供了

ProjectionEvaluator

。该抽象类的接口函数

project()

，以

State

* 为输入，输出Eigen::VectorXd。通过成员函数

setCellSizes()

设置单元规格，即可对欧拉空间实施离散化网格处理。而成员函数

computeCoordinates()

负责生成网格的坐标系。

设置单元规格后须使用

ProjectionEvaluator::setup()

完成配置更新，否则配置不起作用。若未设置单元规格，成员函数

setup()

将通过采样的方式定义规格以使各维度被划分为默认的20份。

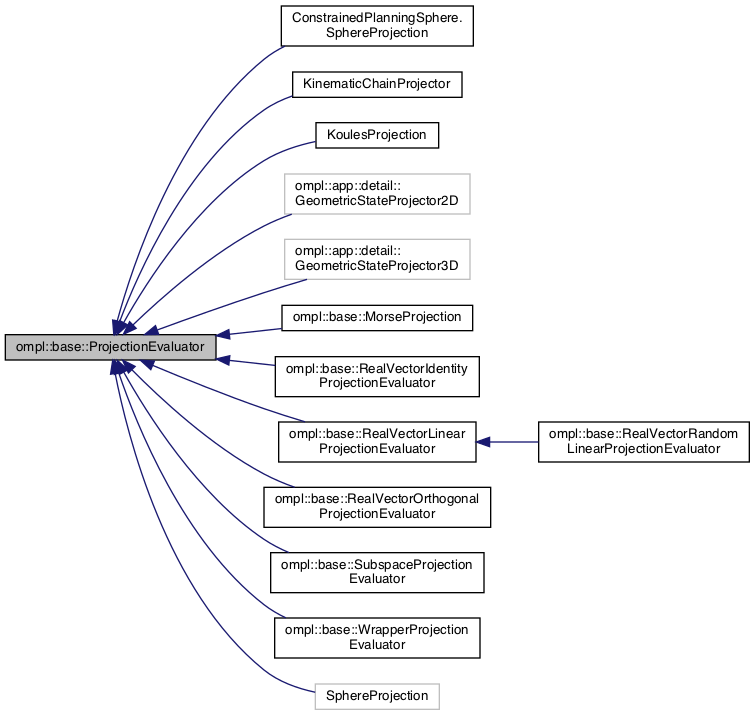
图5

预定义的Projection Evaluator


2.3.2

映射器使用

如果自定义空间存在向欧拉空间的映射(

ompl::base::ProjectionEvaluator

)，可以通过定义

ompl::base::StateSpace::registerProjections()

来向状态空间的映射函数列表std::map< std::string,

ProjectionEvaluatorPtr

>

projections_

注册映射器，推荐将所有映射函数注册至相应的状态空间。

registerProjections()

的实质内容是调用

ompl::base::StateSpace::registerProjection()

或

ompl::base::StateSpace::registerDefaultProjection()

。多数状态空间通过

registerProjections()

设置了一个默认映射函数，如果状态空间没有额外定义映射器，而规划时规划器需使用映射时，将使用默认的映射器。根据实际问题，建议定义更合适的映射函数。 

void ompl::base::RealVectorStateSpace::registerProjections()
{
    // compute a default random projection
    if (dimension_ > 0)
    {
        if (dimension_ > 2)
        {
            int p = std::max(2, (int)ceil(log((double)dimension_)));
            registerDefaultProjection(std::make_shared<RealVectorRandomLinearProjectionEvaluator>(this, p));
        }
        else
            registerDefaultProjection(std::make_shared<RealVectorIdentityProjectionEvaluator>(this));
    }
}
void ompl::base::SE2StateSpace::registerProjections()
 {
     class SE2DefaultProjection : public ProjectionEvaluator
     {
     public:
         SE2DefaultProjection(const StateSpace *space) : ProjectionEvaluator(space)
         {
         }
 
         unsigned int getDimension() const override
         {
             return 2;
         }
 
         void defaultCellSizes() override
         {
             cellSizes_.resize(2);
             bounds_ = space_->as<SE2StateSpace>()->getBounds();
             cellSizes_[0] = (bounds_.high[0] - bounds_.low[0]) / magic::PROJECTION_DIMENSION_SPLITS;
             cellSizes_[1] = (bounds_.high[1] - bounds_.low[1]) / magic::PROJECTION_DIMENSION_SPLITS;
         }
 
         void project(const State *state, Eigen::Ref<Eigen::VectorXd> projection) const override
         {
             projection = Eigen::Map<const Eigen::VectorXd>(
                 state->as<SE2StateSpace::StateType>()->as<RealVectorStateSpace::StateType>(0)->values, 2);
         }
     };
 
     registerDefaultProjection(std::make_shared<SE2DefaultProjection>(this));
 }


注：使用

Projection Evaluator时，还需要注意将规划器中和状态空间中定义的Evaluator

名字保持一致

，如下统一为”myProjection”： 

using namespace ompl;
class MyProjection : public base::ProjectionEvaluator
{
public:
MyProjection(const base::StateSpacePtr &space) : base::ProjectionEvaluator(space)
{
}
virtual unsigned int getDimension(void) const
{
    return 2;
}
virtual void defaultCellSizes(void)
{
    cellSizes_.resize(2);
    cellSizes_[0] = 0.1;
    cellSizes_[1] = 0.25;
}
virtual void project(const base::State *state, Eigen::Ref<Eigen::VectorXd> projection) const
{
    const double *values = state->as<base::RealVectorStateSpace::StateType>()->values;
    projection(0) = (values[0] + values[1]) / 2.0;
    projection(1) = (values[2] + values[3]) / 2.0;
}
};
...
base::StateSpacePtr space;


//方法1
space->registerProjection("myProjection", base::ProjectionEvaluatorPtr(new MyProjection(space)));
...
base::PlannerPtr planner;
planner->as<geometric::KPIECE1>()->setProjectionEvaluator("myProjection");

//方法2，将其注册为默认Projection，则不用在规划器中声明使用的映射器
space->registerDefaultProjection(base::ProjectionEvaluatorPtr(new MyProjection(space)));

2.4 状态的内存申请

//简易方法1
ompl::base::StateSpacePtr space(new T());
ompl::base::ScopedState<> state(space);

//简易方法2
ompl::base::SpaceInformationPtr si(space);
ompl::base::ScopedState<T> state(si);

//高级方法
ompl::base::SpaceInformationPtr si(space);
ompl::base::State* state = si->allocState();
...
si->freeState(state);

2.5 状态空间的使用

ompl::base::StateSpacePtr space(new ompl::base::SE2StateSpace());
ompl::base::ScopedState<ompl::base::SE2StateSpace> state(space);
state->setX(0.1);
state->setY(0.2);
state->setYaw(0.0);
// construct a state that corresponds to the position component of SE2
ompl::base::ScopedState<> pos(space->as<ompl::base::SE2StateSpace>()->getSubspace(0));

ompl::base::ScopedState<> backup = state;
// backup maintains its internal state as State*, so setX() is not available.
// the content of backup is copied from state
ompl::base::State *abstractState = space->allocState();
// this will copy the content of abstractState to state and
// cast it internally as ompl::base::SE2StateSpace::StateType
state = abstractState;
// restore state to it's original value
state = backup;

States can also be printed to streams: 

ompl::base::ScopedState<> state(space);
std::cout << state;

三、

State Validity Checking

（状态评估器）


ompl::base::StateValidityChecker

(单个状态评估)和

ompl::base::MotionValidator

(两状态间运动评估)必须

线程安全

。

3.1 状态评估


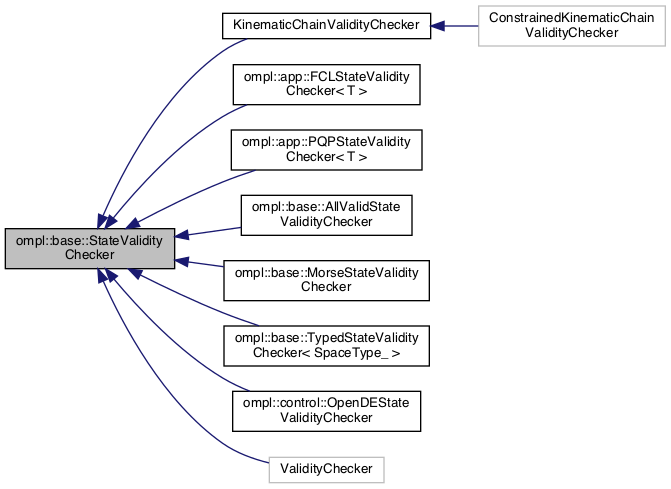
预定义状态评估器：

http://ompl.kavrakilab.org/classompl_1_1base_1_1StateValidityChecker.html

图6

预定义状态评估器


自定义状态评估器：
 

// 1. class way
class myStateValidityCheckerClass : public base::StateValidityChecker
{
public:
     myStateValidityCheckerClass(const base::SpaceInformationPtr &si) :
       base::StateValidityChecker(si)
        {
     }
     //关键函数，实现评估功能
     virtual bool isValid(const base::State *state) const
     {
             return ...;
     }
};
// 2.function way
bool myStateValidityCheckerFunction(const base::State *state)
{
     return ...;
}


状态评估器使用：
 

//默认ompl::base::AllValidStateValidityChecker，即空间中所有state均有效
base::SpaceInformationPtr si(space);
// 1. class way
si->setStateValidityChecker(std::make_shared<myStateValidityCheckerClass>(si));
// 2.function way
si->setStateValidityChecker(myStateValidityCheckerFunction);
si->setStateValidityCheckingResolution(0.03); // 3%
si->setup();

3.2 运动评估


预定义运动评估器：

预定义了

ompl::base::DiscreteMotionValidator

，其分辨率从

ompl::base::StateSpace::validSegmentCount()

获取。

ompl::base::SpaceInformation::setStateValidityCheckingResolution()

设置分辨率(通常为

ompl::base::StateSpace::getMaximumExtent()

的百分比，默认为1%)，calling

ompl::base::StateSpace::setLongestValidSegmentFraction()

for individual state spaces。

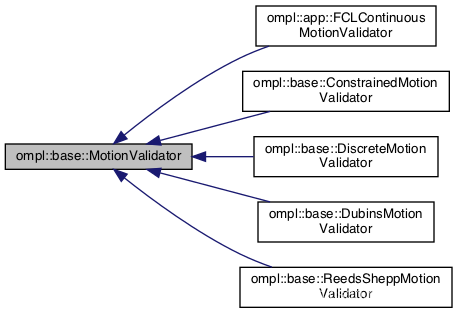
http://ompl.kavrakilab.org/classompl_1_1base_1_1MotionValidator.html

图7

预定义运动评估器


自定义运动评估器：

其中关键函数

ompl::base::MotionValidator::checkMotion()
 

// define this class:
class myMotionValidator : public base::MotionValidator
{
public:
    //This function assumes s1 is valid. Check if the path between two states (from s1 to s2) is valid
    virtual bool checkMotion (const State *s1, const State *s2) const
    {
       ……
    }
    /* This function assumes s1 is valid. Check if the path between two states is valid. 
     * Also compute the last state that was valid and the time of that state. 
     * The time is used to parametrize the motion from s1 to s2, s1 being at t = 0 and s2 being at t = 1
     */
    virtual bool checkMotion (const State *s1, const State *s2, std::pair< State *, double > &lastValid) const
    {
       ……
    }
};


运动评估器使用：
 

base::SpaceInformationPtr si(space);
si->setMotionValidator(std::make_shared<myMotionValidator>(si));
si->setup();

四、

Valid


State Samplers

（采样器）

4.1 预定义采样器

7个预定义的采样器均继承自

ompl::base::ValidStateSampler

，且均内含了StateSampler作为其成员变量。通过评估分析StateSampler的底层采样结果，决策下一步的高层采样方向。因此高度依赖状态空间本身的采样器。


ompl::base::BridgeTestValidStateSampler
 		Take the valid midpoint of a set of two invalid states

ompl::base::ConstrainedValidStateSampler
 		sample for constrained state spaces

ompl::base::GaussianValidStateSampler
 		generate states using a Gaussian distribution

ompl::base::MaximizeClearanceValidStateSampler
 		once it finds a valid state, attempts to find and report another with higher clearance

ompl::base::MinimumClearanceValidStateSampler
 		with extra requirement of min for clearance to nearest obstacle

ompl::base::ObstacleBasedValidStateSampler
 		returns the last state that is valid before reaching an invalid state

ompl::base::UniformValidStateSampler
 		generate uniform samples

4.2 自定义采样器

自定义一个ValidStateSample时：可像4.1中预定义采样器那样定义一个采样器成员并使用其进行底层采样，仅定义高层采样规则；也可从底层开始全部自定义。

ompl::base::SpaceInformation::isValid()

决定样本是否符合约束。自定义采样器及采样器使用示例见

StateSampling.cpp

。两种典型情况的自定义采样器：

  • 如果使用了碰撞检测器，获取了与最近障碍物的距离，甚至包括允许的距离阈值。则自定义一个能利用这些信息的Valid state sampler将极其有用。
  • 如果能直接将状态的约束条件并入采样(而不是将标准ValidStateSampler的采样结果中不符合约束的采样予以丢弃)，性能将获得提升。接下来我们将就此给出示例。

4.3 采样器使用

使用采样器前必须先为其开辟内存，因此必须使用

ompl::base::ValidStateSamplerAllocator

函数或者采样器构造函数make_shared<采样器>(SpaceInformation*)。

StateSampling.cpp节选： 

/*************采样器定义*************/
namespace ob = ompl::base;
namespace og = ompl::geometric;
/// @cond IGNORE
// This is a problem-specific sampler that automatically generates valid
// states; it doesn't need to call SpaceInformation::isValid. This is an
// example of constrained sampling. If you can explicitly describe the set valid
// states and can draw samples from it, then this is typically much more
// efficient than generating random samples from the entire state space and
// checking for validity.
class MyValidStateSampler : public ob::ValidStateSampler
{
public:
    MyValidStateSampler(const ob::SpaceInformation *si) : ValidStateSampler(si)
    {
        name_ = "my sampler";
    }
    // Generate a sample in the valid part of the R^3 state space
    // Valid states satisfy the following constraints:
    // -1<= x,y,z <=1
    // if .25 <= z <= .5, then |x|>.8 and |y|>.8
    bool sample(ob::State *state) override
    {
        double* val = static_cast<ob::RealVectorStateSpace::StateType*>(state)->values;
        double z = rng_.uniformReal(-1,1);
        if (z>.25 && z<.5)
        {
            double x = rng_.uniformReal(0,1.8), y = rng_.uniformReal(0,.2);
            switch(rng_.uniformInt(0,3))
            {
                case 0: val[0]=x-1;  val[1]=y-1;  break;
                case 1: val[0]=x-.8; val[1]=y+.8; break;
                case 2: val[0]=y-1;  val[1]=x-1;  break;
                case 3: val[0]=y+.8; val[1]=x-.8; break;
            }
        }
        else
        {
            val[0] = rng_.uniformReal(-1,1);
            val[1] = rng_.uniformReal(-1,1);
        }
        val[2] = z;
        assert(si_->isValid(state));
        return true;
    }
    // We don't need this in the example below.
    bool sampleNear(ob::State* /*state*/, const ob::State* /*near*/, const double /*distance*/) override
    {
        throw ompl::Exception("MyValidStateSampler::sampleNear", "not implemented");
        return false;
    }
protected:
    ompl::RNG rng_;
};


/*************采样器实例*************/
ob::ValidStateSamplerPtr allocMyValidStateSampler(const ob::SpaceInformation *si)
{
    return std::make_shared<MyValidStateSampler>(si);
}


/*************采样器使用*************/
ss.getSpaceInformation()->setValidStateSamplerAllocator(allocMyValidStateSampler);

五、

目标状态
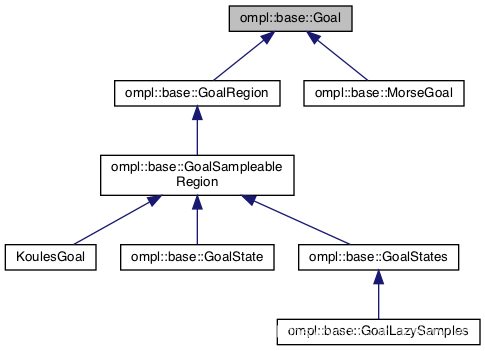
图8

预定义的Goal表现形式

5.1 设置目标

目标的通常表现形式为

ompl::base::Goal

。该类包含一个纯虚函数

ompl::base::Goal::isSatisfied()

，用以判定输入的状态是否为目标。该函数将对是否已进入目标区域作出判定。 

class MyArbitraryGoal : public ompl::base::Goal
{
public:
    MyArbitraryGoal(const SpaceInformationPtr &si) : ompl::base::Goal(si)
    {
    }
    virtual bool isSatisfied(const State *st) const
    {
        // perform any operations and return a truth value
    }
};

上述是一个通用定义，但很多情况下目标包含更多已知信息。这些已知信息对规划器有很大助益，因此使用者应尽可能在目标中描述这些已知信息。 下面是规划器可以使用的信息类型：


5.1.1

如果到目标的大致距离(不要求必须是度量标准)可获取，该距离信息可通过

ompl::base::Goal::isSatisfied()

的重载形式(输入参数为状态和距离)传给规划器。默认情况下，函数内部将该距离设置为double类型所能表现的最大值。 

class MyArbitraryGoal : public ompl::base::Goal
{
public:
    MyArbitraryGoal(const SpaceInformationPtr &si) : ompl::base::Goal(si)
    {
    }
    virtual bool isSatisfied(const State *st) const
        {
        perform_any_operations();
        return truth value;
    }
    virtual bool isSatisfied(const State *st, double *distance) const
        {
        bool result = isSatisfied(st);
        if (distance != NULL)
        {
            if (state_clearly_out_of_goal_region(st))
                    {
                *distance = std::numeric_limits<double>::max();
            }
            else
            {
                if (state_near_goal(st))
                    *distance = 1;
                else
                    *distance = 100;
            }
        }
        return result;
    }
};


5.1.2

很多情况下，距目标范围的距离可获得，某状态在目标区域内的条件是该距离比规定的阈值小。该情况下，应使用

ompl::base::GoalRegion

(继承自

Goal

)，同时其附加的

ompl::base::GoalRegion::distanceGoal()

应被定义。通过比较

distanceGoal()

的返回值与规定的阈值(默认为机器精度)，实现各重载形式的

isSatisfied()

。 

class MyGoalRegion : public ompl::base::GoalRegion
{
public:
    MyGoalRegion(const SpaceInformationPtr &si) : ompl::base::GoalRegion(si)
    {
        setThreshold(0.1);
    }
    virtual double distanceGoal(const State *st) const
        {
        // perform any operations and return a double indicating the distance to the goal
    }
};


5.1.3

双向规划器工作时需获取在目标区域内的所有状态。如果存在对目标区域采样的方法，应使用类

ompl::base::GoalSampleableRegion

(继承自

ompl::base::GoalRegion

)。该类定义了两个附加函数：

ompl::base::GoalSampleableRegion::sampleGoal()

和

ompl::base::GoalSampleableRegion::maxSampleCount()

。此二函数分别实现规划器从目标区域内采样，及给出目标区域内最多容纳有多少不同的样本。注：别忘了

ompl::base::GoalRegion::distanceGoal()

仍需定义。

此时，双向规划器无须核对某状态是否在目标区域中，因为其规划始于目标区域中的状态，故

isSatisfied()

也不再被调用。取而代之的是，当建立起连接树后，

ompl::base::Goal::isStartGoalPairValid()

被调用。该函数默认返回true，作用是当连接至特定的目标状态时，告知规划器是否需要特定的起始状态来建立有效的路径。通常无须重写该函数。为方便起见，提供了一些

GoalSampleableRegion

的衍生形式：

5.2 目标区域的使用

规划器将规定的目标形式映射为规划器能使用的最小化形式。对于单向规划器，

ompl::base::Goal

即可。而对于双向规划器，必须是

ompl::base::GoalSampleableRegion

。

如果规划器可以使用规定的目标，它将进行运动规划的计算。如果运算成功，发现的路径被存放至该目标区域，指示规划结果是否已接近的标志量将被置位。所有经规划器使用

Goal

的访问器设置的信息，均可供使用者查询 。

<!–  包含路径长度概念的规划器尝试寻找更短的路径解，过程中使用

isSatisfied()

的第三种重载形式(传参为路径长度)。该重载形式判定是否遭遇最大路径长度。使用者可以调用ompl::base::Goal::setMaximumPathLength()设置最大路径长度。  –>该部分内容于新版本中已删去。

六、

路径可视化

打印路径规划结果矩阵到文件。两种路径形式

ompl::geometric::PathGeometric

(路径)和

ompl::control::PathControl

(轨迹)均

提供printAsMatrix()函数，每行是一个状态点，姿态为单位四元数形式。轨迹

contains the controls and control duration needed to reach the state in this row starting from the state in the previous row (the controls and duration in the first row are all zeros)

6.1 路径输出

bool solved = ss.solve(20.0); // ss is a SimpleSetup object
if (solved)
    ss.getSolutionPath().printAsMatrix(std::cout);

6.2 轨迹的路径输出

bool solved = ss.solve(20.0); // ss is a SimpleSetup object
if (solved)
    ss.getSolutionPath().asGeometric().printAsMatrix(std::cout);

七、

Benchmark Planners

7.1 步骤

  • Configure the benchmark problem using

    ompl::geometric::SimpleSetup

    or

    ompl::control::SimpleSetup
  • Create a ompl::Benchmark object that takes the problem as input
  • Optionally, specify some parameters for the benchmark object using ompl::Benchmark::addExperimentParameter, which is useful when aggregating benchmark results over parametrized benchmarks.
  • Add one or more planners to the benchmark
  • Optionally add events to be called before and/or after the execution of a planner
  • Run the benchmark problem a specified number of times, subject to specified time and memory limits

7.2 代码示例

#include "ompl/tools/benchmark/Benchmark.h"
// A function that matches the ompl::base::PlannerAllocator type.
// It will be used later to allocate an instance of EST
ompl::base::PlannerPtr myConfiguredPlanner(const ompl::base::SpaceInformationPtr &si)
{
    geometric::EST *est = new ompl::geometric::EST(si);
    est->setRange(100.0);
    return ompl::base::PlannerPtr(est);
}
// Create a state space for the space we are planning in
ompl::geometric::SimpleSetup ss(space);
// Configure the problem to solve: set start state(s)
// and goal representation
// Everything must be set up to the point ss.solve()
// can be called. Setting up a planner is not needed.


/*Benchmarking code starts here: */
// First we create a benchmark class:
ompl::tools::Benchmark b(ss, "my experiment");
// Optionally, specify some benchmark parameters (非运行参数，只是说明性名称)
b.addExperimentParameter("num_dofs", "INTEGER", "6")
b.addExperimentParameter("num_obstacles", "INTEGER", "10")
// We add the planners to evaluate.
b.addPlanner(base::PlannerPtr(new geometric::KPIECE1(ss.getSpaceInformation())));
b.addPlanner(base::PlannerPtr(new geometric::RRT(ss.getSpaceInformation())));
b.addPlanner(base::PlannerPtr(new geometric::SBL(ss.getSpaceInformation())));
b.addPlanner(base::PlannerPtr(new geometric::LBKPIECE1(ss.getSpaceInformation())));
// etc
// For planners that we want to configure in specific ways,
// the ompl::base::PlannerAllocator should be used:
b.addPlannerAllocator(std::bind(&myConfiguredPlanner, std::placeholders::_1));
// etc.
// Now we can benchmark: 5 second time limit for each plan computation,
// 100 MB maximum memory usage per plan computation, 50 runs for each planner
// and true means that a text-mode progress bar should be displayed while
// computation is running.
ompl::tools::Benchmark::Request req;
req.maxTime = 5.0;
req.maxMem = 100.0;
req.runCount = 50;
req.displayProgress = true;
b.benchmark(req);
// This will generate a file of the form ompl_host_time.log
b.saveResultsToFile();


/*Adding callbacks for before and after the execution of a run is also possible: */
// Assume these functions are defined
void optionalPreRunEvent(const base::PlannerPtr &planner)
{
    // do whatever configuration we want to the planner,
    // including changing of problem definition (input states)
    // via planner->getProblemDefinition()
}
void optionalPostRunEvent(const base::PlannerPtr &planner, tools::Benchmark::RunProperties &run)
{
    // do any cleanup, or set values for upcoming run (or upcoming call to the pre-run event).
    // adding elements to the set of collected run properties is also possible;
    // (the added data will be recorded in the log file)
    run["some extra property name INTEGER"] = "some value";
    // The format of added data is string key, string value pairs,
    // with the convention that the last word in string key is one of
    // REAL, INTEGER, BOOLEAN, STRING. (this will be the type of the field
    // when the log file is processed and saved as a database).
    // The values are always converted to string.
}
// After the Benchmark class is defined, the events can be optionally registered:
b.setPreRunEvent(std::bind(&optionalPreRunEvent, std::placeholders::_1));
b.setPostRunEvent(std::bind(&optionalPostRunEvent, std::placeholders::_1, std::placeholders::_2));

以上setPreRunEvent和setPostRunEvent应该不需要bind吧，其参数本就是function，支持函数指针啊？

完整示例链接


7.3 处理日志

首先均需要生成db文件： 

ompl/scripts/ompl_benchmark_statistics.py logfile.log -d mydatabase.db

方法1：将db文件导入网页工具

Planner Arena进行浏览

方法2：从db文件生成包含分析图表的pdf 

ompl/scripts/ompl_benchmark_statistics.py -d mydatabase.db -p boxplot.pdf

方法3：生成sql文件，导入其它软件查看 

ompl/scripts/ompl_benchmark_statistics.py -d mydatabase.db -m mydump.sql

–ompl_benchmark_statistics.py工具使用帮助 

scripts/ompl_benchmark_statistics.py --help

八、

Optimal Planning

（最优化）

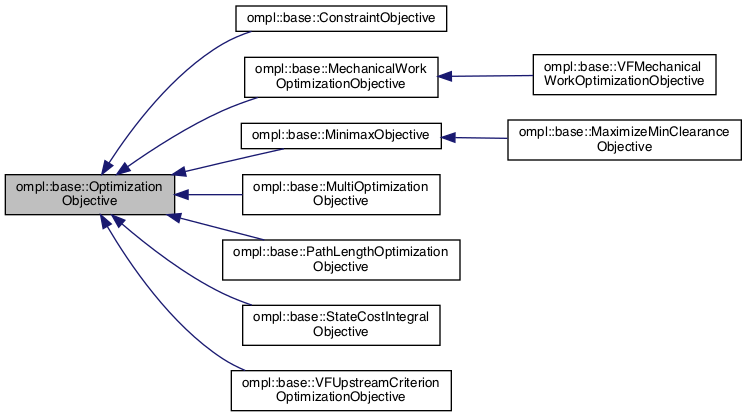
在一些运动规划问题中，不仅要得到起点到终点的路径，可能还关注路径最短或者路径离障碍最远。因此目标可能是一个经优化的路径：由起点到终点无碰撞且某些方面经过优化的路径(如路径长度或路径净空)。将含有类似优化操作的运动规划器称为优化规划器。

OMPL还支持

CForest

平行化框架，可以加速优化运动规划器的收敛。

了解更多关于CForest内容

。

8.1 与一般运动规划的主要不同

  • 为


    ompl::base::ProblemDefinition


    定义优化对象

    ompl::base::OptimizationObjective

    (比如最短路径，离障碍物最远的路径等)。一些预定义的优化对象如路径长度、最小路径净空、路径的状态累积消耗、机械功，它们都定义了路径消耗概念(机器人位形空间中随运动而增加的量)。OMPL允许使用者通过


    ompl::base::MultiOptimizationObjective



    合并优化目标以实现运动规划的

    多目标优化

    。
  • 必须使用优化规划算法。关于优化规划器，OMPL目前提供一些规划器确保结果的渐进优化性(前言2.1.3中

    Optimizing planners

    列表)。更多关于运动规划中的渐进优化可阅读Karaman的

    论文

    。

图9

预定义优化对象

8.2

局限性

为最大化计算效率，OMPL将路径消耗用一个double值表示。多数优化规划问题中，该double值足以全面描述优化对象，即使优化对象是多目标时。多目标优化问题中，可以将路径的各优化对象的消耗进行加权求和得double值。

但是仍存在一些优化问题无法用单个double值表示。例如不能合并最短路径和最大化净空这两个优化目标。因为路径长度和最小空隙需分别用两个值记录路径消耗的累积。因此无法用单double形式描述的多目标优化问题，其各优化对象无法共用一个累积消耗方程。此例可以被看为路径长度对象和状态消耗积分对象的合并，其中状态消耗是净空的方程。

注：因为

PathLengthOptimizationObjective

从

OptimizationObjective

继承的

isCostBetterThan

( )函数优化目标是最小化消耗，而

MaximizeMinClearanceObjective

的

isCostBetterThan

( )函数是最大化消耗，这两个相反的优化消耗方向无法合并。

8.3 示例

边界为(0,0)，(1,1)的正方形R2空间，在(0.5,0.5)处有一个半径为0.25的圆形区域障碍。使用


ompl::base::RealVectorStateSpace

(2)。


8.3.1 评估器：
 

// Our collision checker. For this demo, our robot's state space
// lies in [0,1]x[0,1], with a circular obstacle of radius 0.25
// centered at (0.5,0.5). Any states lying in this circular region are
// considered "in collision".
class ValidityChecker : public ob::StateValidityChecker
{
public:
    ValidityChecker(const ob::SpaceInformationPtr& si) :
        ob::StateValidityChecker(si) {}
    // Returns whether the given state's position overlaps the
    // circular obstacle
    bool isValid(const ob::State* state) const
    {
        return this->clearance(state) > 0.0;
    }
    // Returns the distance from the given state's position to the
    // boundary of the circular obstacle.
    double clearance(const ob::State* state) const
    {
        // We know we're working with a RealVectorStateSpace in this
        // example, so we downcast state into the specific type.
        const ob::RealVectorStateSpace::StateType* state2D =
            state->as<ob::RealVectorStateSpace::StateType>();
        // Extract the robot's (x,y) position from its state
        double x = state2D->values[0];
        double y = state2D->values[1];
        // Distance formula between two points, offset by the circle's
        // radius
        return sqrt((x-0.5)*(x-0.5) + (y-0.5)*(y-0.5)) - 0.25;
    }
};


8.3.2 状态空间设置：
 

// Construct the robot state space in which we're planning. We're
// planning in [0,1]x[0,1], a subset of R^2.
ob::StateSpacePtr space(new ob::RealVectorStateSpace(2));
// Set the bounds of space to be in [0,1].
space->as<ob::RealVectorStateSpace>()->setBounds(0.0, 1.0);
// Construct a space information instance for this state space
ob::SpaceInformationPtr si(new ob::SpaceInformation(space));
// Set the object used to check which states in the space are valid
si->setStateValidityChecker(ob::StateValidityCheckerPtr(new ValidityChecker(si)));
si->setup();
// Set our robot's starting state to be the bottom-left corner of
// the environment, or (0,0).
ob::ScopedState<> start(space);
start->as<ob::RealVectorStateSpace::StateType>()->values[0] = 0.0;
start->as<ob::RealVectorStateSpace::StateType>()->values[1] = 0.0;
// Set our robot's goal state to be the top-right corner of the
// environment, or (1,1).
ob::ScopedState<> goal(space);
goal->as<ob::RealVectorStateSpace::StateType>()->values[0] = 1.0;
goal->as<ob::RealVectorStateSpace::StateType>()->values[1] = 1.0;
// Create a problem instance
ob::ProblemDefinitionPtr pdef(new ob::ProblemDefinition(si));
// Set the start and goal states
pdef->setStartAndGoalStates(start, goal);


8.3.3 实例化优化对象的函数，开辟内存空间，返回shared_ptr：
 

// Returns a structure representing the optimization objective to use
// for optimal motion planning. This method returns an objective which
// attempts to minimize the length in configuration space of computed
// paths.
ob::OptimizationObjectivePtr getPathLengthObjective(const ob::SpaceInformationPtr& si)
{
    //优化目标为最短路径，默认阈值为0
    return ob::OptimizationObjectivePtr(new ob::PathLengthOptimizationObjective(si));
}

pdef->setOptimizationObjective(getPathLengthObjective(si));


8.3.4 规划器：
 

// Construct our optimizing planner using the RRTstar algorithm. 
//RRT*的默认优化目标为最短路径，因此若非其它优化目标，可不设置而直接采用默认值。
ob::PlannerPtr optimizingPlanner(new og::RRTstar(si));
// Set the problem instance for our planner to solve
optimizingPlanner->setProblemDefinition(pdef);
optimizingPlanner->setup();
// attempt to solve the planning problem within one second of
// planning time
ob::PlannerStatus solved = optimizingPlanner->solve(1.0);


8.3.5 优化过程显示：

图10 优化过程示意图

最优化规划器直至寻找到满足最优化对象要求的路径才结束（或直至所给时限）。由于示例中未定义阈值，使用了默认阈值0，故永远无法达到优化目标，将直至solve中给定的时限。


8.3.6 优化阈值设置

区别于8.3.3中getPathLengthObjective()函数直接开辟对象内存将生成的shared_ptr返回不同，此处在生成对象后，对其进行阈值设置setCostThreshold()后再将其返回。setCostThreshold()将阈值封装至


ompl::base::Cost

对象。
 

ob::OptimizationObjectivePtr getThresholdPathLengthObj(const ob::SpaceInformationPtr& si)
{
    ob::OptimizationObjectivePtr obj(new ob::PathLengthOptimizationObjective(si));
    obj->setCostThreshold(ob::Cost(1.51));
    return obj;
}


注：当设置一个无法达到的优化阈值时，规划器将给出于时限耗尽内计算得到的最优化结果 。


8.3.7

完整示例

8.4

自定义优化对象

在几何规划中，起始和终止状态充分地定义了运动。默认情况下，8.1中的优化对象试图最小化路径消耗，但该性能是可以被自定义的。我们假设整条路径的消耗可被分解为组成路径的最小运动单元的消耗累积，累积的方法(如求和，乘法)可被自定义。


8.4.1 路径净空

在前述例子中，最短路径距中心圆障碍物很近，造成安全隐患。为确保安全，使路径远离障碍物。因此选择路径净空作为状态消耗沿路径的累积，每个状态的消耗是该状态距障碍距离的方程。我们使用


ompl::base::StateCostIntegralObjective

作为基类，因其按照需求将优化对象表示为状态消耗的累积。至此，我们只需重写

ompl::base::OptimizationObjective::stateCost()

函数以描述状态消耗方程即可。
 

class ClearanceObjective : public ob::StateCostIntegralObjective
{
public:
    ClearanceObjective(const ob::SpaceInformationPtr& si) :
        ob::StateCostIntegralObjective(si, true)
    {
    }
    ob::Cost stateCost(const ob::State* s) const
    {
        return ob::Cost(1 / si_->getStateValidityChecker()->clearance(s));
    }
};

优化对象默认寻找最小化路径消耗。而针对路径净空对象，我们希望其最大化。因此将状态消耗定义为状态净空的倒数。


ClearanceObjective的构造函数中，我们除使用


SpaceInformationPtr

外，还使用了true初始化

StateCostIntegralObjective

。这是为了使优化对象在沿路径累加状态消耗时，使用运动消耗插值。默认情况下，


StateCostIntegralObjective

的


motionCost (const State *s1, const State *s2)


简单地采用
$\begin{eqnarray*} \mbox{cost} &=& \frac{cost(s_1) + cost(s_2)}{2}\vert s_1 - s_2 \vert \end{eqnarray*}$
计算这段路径的消耗。但这种方式面对路径上状态间距过大的情况时，将可能错误地估计路径消耗。如果

我们允许运动消耗插值，路径消耗计算将在间距大的状态间插值以获得更为准确的实际路径消耗近似。此

沿路径的状态插值

与


DiscreteMotionValidator

中

使用的方法

完全相同。该运动消耗插值计算法在提高精确度的同时将降低了运算效率，因为更多次地调用

ompl::base::OptimizationObjective::stateCost

。

图11 RRT*规划最大净空的动态过程演示


8.4.2 最小净空最大化

下面定义一个利用了


OptimizationObjective


中更多接口函数的优化对象，将路径最小净空最大化作为优化目标。给定路径的消耗被定义为表示路径和障碍间的最近距离。该优化对象其实已存在预定义的实现方式


ompl::base::MaximizeMinClearanceObjective


。此处我们着手将其实现一遍： 

class MaximizeMinClearance : public ob::OptimizationObjective
{
public:
    MaximizeMinClearance(const ob::SpaceInformationPtr &si) :
        ob::OptimizationObjective(si) {}
    virtual ob::Cost stateCost(const ob::State* s) const;
    virtual bool isCostBetterThan(ob::Cost c1, ob::Cost c2) const;
    virtual ob::Cost motionCost(const ob::State *s1, const ob::State *s2) const;
    virtual ob::Cost combineCosts(ob::Cost c1, ob::Cost c2) const;
    virtual ob::Cost identityCost() const;
    virtual ob::Cost infiniteCost() const;
};

与8.4.1类似，我们可以通过定义单个状态的消耗来定义整条路径的消耗： 

ob::Cost MaximizeMinClearance::stateCost(const ob::State* s) const
{
    return ob::Cost(this->si_->getStateValidityChecker()->clearance(s));
}

8.4.1中定义为净空的倒数是因为我们局限于将优化方向默认为最小化路径消耗(这样我们可以充分利用


StateCostIntegralObjective


已定义的函数)。其实我们同样可以通过重写


isCostBetterThan()



函数

把优化方向变为最大化消耗(以此得到最大化净空)： 

bool MaximizeMinClearance::isCostBetterThan(ob::Cost c1, ob::Cost c2) const
{
    return c1.value() > c2.value() + ompl::magic::BETTER_PATH_COST_MARGIN;
}

优化规划器使用该函数选取更优的路径。该函数的输出bool表示c1消耗是否优于c2（cost实际是对double类型的简单封装，通过

ompl::base::Cost::v即可访问该double值

），此处表现为c1的值大于c2。比较中可能包含了附加阈值以在优化规划器中融入数值鲁棒性。重写


isCostBetterThan()

函数时最好使用一个这样的阈值。



注

：上述对double进行

ompl::base::Cost

类封装而非使用typedef是为了类型安全性。如果仅仅是typedef，使用者可能不经意间使用了符号<而非

isCostBetterThan()

，这将导致难以发现的错误。通过这层类封装，编译器将捕获到此错误。

这种编程习惯应该学习。

从某种程度上说，最大化最小净空可以用与先前优化对象相似的公式表示。路径是状态序列，路径消耗可以被表示为沿路径采用特有的方式合并状态消耗。在前例中，该合并方式为相加。而对应到最小净空，该合并方式即为取小函数。我们可以通过重写


ompl::base::OptimizationObjective::combineCosts

函数实现该功能：
 

ob::Cost MaximizeMinClearance::combineCosts(ob::Cost c1, ob::Cost c2) const
{
    if (c1.value() < c2.value())
        return c1;
    else
        return c2;
}

该函数于基类


ompl::base::OptimizationObjective

中的表现形式即为对两传参进行简单相加。在本例中，我们将两传参中较小的返回，等效于将两者中的最小净空返回。如果

我们使用该操作而非加法累计路径消耗，即可按期望得到整个路径的最小净空。

接下来我们需要指定如何计算由运动的起始点定义的运动的消耗。运动的消耗源自运动中整个状态的连续体的最小净空。在许多真实情况下的运动规划问题中，该运动消耗很难计算，故我们只能采用某种近似。一种近似即简单地采用起始点净空的小值，我们将其作为简易示例。但对运动进行状态插值采样将获得更高的精度，比如

ompl::base::MinimaxObjective::motionCost

。

下面是我们如何进行起始点运动消耗的近似： 

ob::Cost MaximizeMinClearance::motionCost(ob::State *s1, ob::State *s2) const
{
    return this->combineCosts(this->stateCost(s1), this->stateCost(s2));
}

可以看到该简单近似法用到了前面定义的

combineCost()和stateCost()

函数。

很多优化规划器依赖于其优化对象拥有准确的消耗值，并且该消耗值还具备某些特性。一种普遍的消耗值为

恒等消耗值

。该消耗值c0在与任意其它消耗值c1合并时始终返回c1。比如，当combineCost为简单地相加时，恒等消耗值为0。我们可以通过重写

ompl::base::OptimizationObjective::identityCost( )

函数来描述恒等消耗。如果combineCost为取小运算时，恒等消耗应大于任意其它消耗，即无穷大： 

ob::Cost MaximizeMinClearance::identityCost() const
{
    return ob::Cost(std::numeric_limits<double>::infinity());
}

我们将最小化路径净空对象的恒等消耗定义为无穷大，即采用最大的

double

值初始化该

Cost

对象。

另一种优化规划器普遍使用的消耗值为极限消耗，其劣于所有其它消耗。换句话说，

无论c为何值，

其值c_i 均使得

isCostBetterThan(c_i, c)返回false。针对最小净空对象这一情形(此处cost代表最小净空，值越大越好)，我们可以令极限消耗为负无穷大。

我们可以通过重写


ompl::base::OptimizationObjective::infiniteCost

函数实现该功能：
 

ob::Cost MaximizeMinClearance::infiniteCost() const
{
    return ob::Cost(-std::numeric_limits<double>::infinity());
}

至此，优化对象已可用于规划。在8.3的示例中，我们使用


ompl::geometric::RRTstar

规划器进行优化规划。你会发现当使用

ompl::geometric::PRMstar

规划器求解该问题时将获得更优的结果。当已定义求解问题及优化对象后，可通过如下代码调用：
 

ob::PlannerPtr planner(new og::PRMstar(si));
planner->setProblemDefinition(pdef);
planner->setup();
ob::PlannerStatus solved = planner->solve(timeLimit);


8.4.3 消耗启发式

一些优化运动规划器，如


ompl::geometric::PRMstar

，当结合消耗启发式时将使规划更有效率。启发式是一种快速计算某些值近似的函数。OMPL中定义了两种消耗启发式：


  • 运动消耗启发式，估计两给定状态间优化路径的消耗。

  • Cost-to-go

    启发式，估计给定状态与目标间的

    优化路径的消耗。


通过为优化规划器提供获取更多有关求解问题信息的快捷方法，从而实现优化对象的消耗启发式定义，最终加速规划进程，。


容许性启发式

为使优化规划器能最有效地使用消耗启发式，消耗启发式必须包含名为容许性的重要性质 。一个容许性消耗启发式始终低估路径消耗。亦即，如果路径的真实优化消耗是c_o， 容许启发式返回的c_h永远不会使

isCostBetterThan(c_o, c_h)返回true。



运动消耗启发式

我们思考一个容许性运动消耗启发式在规划2维质点机器人的最短路径时将如何表现。两点之间线段最短。我们可以使用


ompl::base::SpaceInformation::distance


快速计算该路径的距离

。例中由于环境中障碍物的存在使得两点间的真实优化路径更长。但是我们至少可以确保

ompl::base::SpaceInformation::distance

返回的值不会超过真实优化路径的长度。因此，

ompl::base::SpaceInformation::distance

是容许启发式。

下面是


motionCostHeuristic()

的实现方式：
 

ompl::base::Cost
ompl::base::PathLengthOptimizationObjective::motionCostHeuristic(const State *s1,
                                                                 const State *s2) const
{
    return Cost(si_->distance(s1, s2));
}



motionCostHeuristic

的

默认实现方式为返回对象的恒等消耗，对大部分优化对象而言，这是容许启发式。但是，这并不是运动消耗的较精确近似，运动规划器仅在启发式非常接近运动消耗时才大幅加速。因此，如果你的运动规划问题存在更精确、计算更快的容许启发式，建议重写


motionCostHeuristic


以定义一个更合适的。


Cost-to-go 启发式

通过迅速估计给定状态与目标间的优化路径消耗，Cost-to-go启发式可为规划器提供更多信息。但Cost-to-go启发式的定义方式与运动消耗启发式不同：我们必须使用

ompl::base::OptimizationObjective::setCostToGoHeuristic

为优化对象

提供一个函数指针

，而不是像运动消耗启发式一样通过重写函数。使用函数指针很有必要，因为一个优化对象可能被许多不同的目标类型(比如目标是集合)使用而使得启发式计算方式不同。与运动消耗启发式一样，当提供的Cost-to-go启发式为容许的，并且是给定状态与目标间实际优化路径消耗的充分近似时，优化规划器才最高效。

接下来讨论如何在二维质点机器人问题中使用Cost-to-go启发式。假设优化对象为最小化路径长度。此例中，目标被定义为与某指定目标状态间的距离的差值在给定的容许值内的所有状态。因此，指定状态与目标间可能的最短路径等于两状态间直线距离减去容许偏差。此为基于Cost-to-go距离的容许启发式，且已将其用


ompl::base::goalRegionCostToGo



定义：
 

ompl::base::Cost ompl::base::goalRegionCostToGo(const State* state, const Goal* goal)
{
    const GoalRegion* goalRegion = goal->as<GoalRegion>();
    // Ensures that all states within the goal region's threshold to
    // have a cost-to-go of exactly zero.
    return Cost(std::max(goalRegion->distanceGoal(state) - goalRegion->getThreshold(),
                         0.0));
}

该cost-to-go启发式函数可处理任意

ompl::base::GoalRegion

目标类型，因为这些目标类型采用

ompl::base::GoalRegion::distanceGoal

定义目标距离。我们需要在cost-to-go计算结果中减去目标区域的阈值，因为从给定状态至目标的路径不是到目标区域中心而是到区域边缘。最后，我们使用std::max以确保不会返回负消耗。我们可以使用以下函数，创建一个使用该cost-to-go启发式的路径长度优化对象： 

ob::OptimizationObjectivePtr getPathLengthObjWithCostToGo(const ob::SpaceInformationPtr& si)
{
    ob::OptimizationObjectivePtr obj(new ob::PathLengthOptimizationObjective(si));
    obj->setCostToGoHeuristic(&ob::goalRegionCostToGo);
    return obj;
}

特别注意，只有当

ompl::base::GoalRegion::distanceGoal

是一个从某状态沿优化路径到目标区域的消耗的容许启发式时

，

ompl::base::goalRegionCostToGo

启发式才适用于

规划问题

。例如，如果使用


ompl::base::MaximizeMinClearanceObjective

以最大化最小路径净空，

ompl::base::goalRegionCostToGo

函数不是一个合适的cost-to-go启发式，因为

ompl::base::GoalRegion::distanceGoal

与路径净空不相关。

8.5


多目标优化规划


某些情况下，优化规划的优化对象可能不只一个，比如在路径净空和路径长度间寻找平衡。这时可以使用


ompl::base::MultiOptimizationObjective

类。
 

//复杂方式
ob::OptimizationObjectivePtr getBalancedObjective(const ob::SpaceInformationPtr& si)
{
    ob::OptimizationObjectivePtr lengthObj(new ob::PathLengthOptimizationObjective(si));
    ob::OptimizationObjectivePtr clearObj(new ClearanceObjective(si));
    ob::MultiOptimizationObjective* opt = new ob::MultiOptimizationObjective(si);
    opt->addObjective(lengthObj, 10.0);
    opt->addObjective(clearObj, 1.0);
    return ob::OptimizationObjectivePtr(opt);
}

//简单方式，更直观
ob::OptimizationObjectivePtr getBalancedObjective(const ob::SpaceInformationPtr& si)
{
    ob::OptimizationObjectivePtr lengthObj(new ob::PathLengthOptimizationObjective(si));
    ob::OptimizationObjectivePtr clearObj(new ClearanceObjective(si));
    return 10.0*lengthObj + clearObj;
}

上述代码片段创建了一个同时优化路径长度和净空的优化对象。首先实例化各优化对象，然后将它们添加至


MultiOptimizationObjective

，添加时须按其在优化规划中的重要性给定加权系数。这就实现了优化对象的路径消耗是各单独优化对象的路径消耗的和。上例中，路径长度的加权系数被设定为10.0，路径净空加权系数被设定为1.0，更倾向于最小化路径长度。相较于图11，优化结果虽保持了与中央圆之间的净空，但净空性降低。

图12 RRT*规划综合优化对象的动态过程演示

8.6

CForest 并行框架

M.Otte和N. Correll在

论文

中提出CForest。

CForest的中心思想是在起点和目标间并行建立众多数。CForest的关键概念：

  • 每当某棵树找到更优解，立即将其分享至其它树，这样所有树均享有目前找到的最优解。
  • 树均扩散至有利的区域。不能导向更优解的采样将被迅速抛弃。
  • 每当更优的解被发现，树均被修剪。所有树中不能帮助寻找到更优解的状态均被从树移除。

CForest被设计为被任意随机查找树算法使用是基于下列假设：

  1. 查找树大致向优化解方向可靠收敛。
  2. 构形空间遵守

    三角不等式

    。换言之，存在某容许启发法。


8.6.1 OMPL中的CForest

CForest被OMPL纳入作为优化规划器，名为

ompl::geometric::CForest

.

CForest被设计用来优化路径长度。在OMPL中， 任意优化对象均可被优化。因此，CForest 在OMPL中不是被用于状态空间而是优化对象，故优化对象需包含容许启发法。 因为这比较复杂难以检测，故当状态空间非度量空间时将发出警告（不过这并不意味着该优化对象不能被用于CForest）。

目前RRT*(

ompl::geometric::RRTstar

)是唯一可被用于CForest的规划器。因为其是唯一的单一查询，递增的，渐近的OMPL优化规划算法。

CForest规划器将协调不同树并共享发现的解。路径共享是通过定义的CForet状态采样器(

ompl::base::CForestStateSampler

)实现的。该采样器封装了与CForest正在规划的状态空间关联的默认采样器。调用采样方法时，该采样器封装将被掠过，但当某线程发现新的更优解时，随后的调用采样方法步骤将返回沿既有最优路径后续的状态。该操作将用于所有除找到该更优解的线程。

可以像使用其它规划算法那样使用CForest： 

#include <ompl/geometric/planners/cforest/CForest.h>
...
// Setting up the planning problem with SimpleSetup
SimpleSetup ss;
...
ompl::base::PlannerPtr planner(new ompl::geometric::CForest(ss.getSpaceInformation()));
ss.setPlanner(planner);
...

默认情况下，它将在计算机内核允许的范围内使用尽可能多的RRT*实例。实例的数量以及规划器类型可以通过调用addPlannerInstances<T>()函数设置： 

ompl::base::PlannerPtr planner(new ompl::geometric::CForest(ss.getSpaceInformation()));
// Setting up CForest to expand 5 trees of RRTstar.
planner->as<ompl::geometric::CForest>()->addPlannerInstances<ompl::geometric::RRTstar>(5);

addPlannerInstances<T>()的调用将检查规划器类型提供的

PlannerSpecs

。CForest仅支持canReportIntermediateSolutions定为true的那些规划器。否则，执行时将发出以下警告（用PRM*作为示例）： 

planner->as<ompl::geometric::CForest>()->addPlannerInstances<ompl::geometric::PRMstar>(2);
Warning: PRMstar cannot report intermediate solutions, not added as CForest planner.
         at line 100 in ompl/geometric/planners/cforest/CForest.h

如果没有手动添加规划器，将默认设置两RRT*实例。

或者，仅可以定义线程数，而默认选择RRT*作为规划器。在经基准配置文件使用规划器时，这尤其有用： 

// Using 6 threads of the default planner
planner->as<ompl::geometric::CForest>()->setNumThreads(6);

注：该规划器没有适用的Python封装，因为其涉及多线程实施。


8.6.2 与论文版本最主要的不同

实施CForest时，关注点在于将其基层规划器修改得尽可能小。尽管CForest的主旨还在，实际实现方式与论文中提出的不同：

  • 没有使用信息传递。改为使用共享内存和std::thread线程。
  • 论文提出了两种不同的方式：顺序的（树均在同一个CPU内扩展）和并行的（每个CPU一棵树）。而由于程序使用了std::thread，每CPU承载的树的数量由调度器决定。
  • 论文中，对待共享状态与对待随机采样状态略有不同。由于CForestStateSampler封装，所有状态被同样对待。某些情况下，共享状态不被其它树纳入。然而，测试发现这并未对性能产生较大影响。
  • 没有明确规定采样范围。当产生新采样时，我们检测其是否能导向更优解。
  • 为简化代码，起始和目标状态未包含在共享路径中。
  • 在修剪一棵树前，会检查将移除多少状态。如果新树大小比上旧树大小的比例不够小，修剪将不被执行。这降低了移除状态时重新建立NearestNeighbors数据结构的分摊成本。

注：除以上区别外，CForest的使用大幅提高了基层规划器的性能。然而，一种更接近论文描述的方式可以提高性能。在对比你的算法与CForest时，请将这考虑在内。


8.6.3 示例


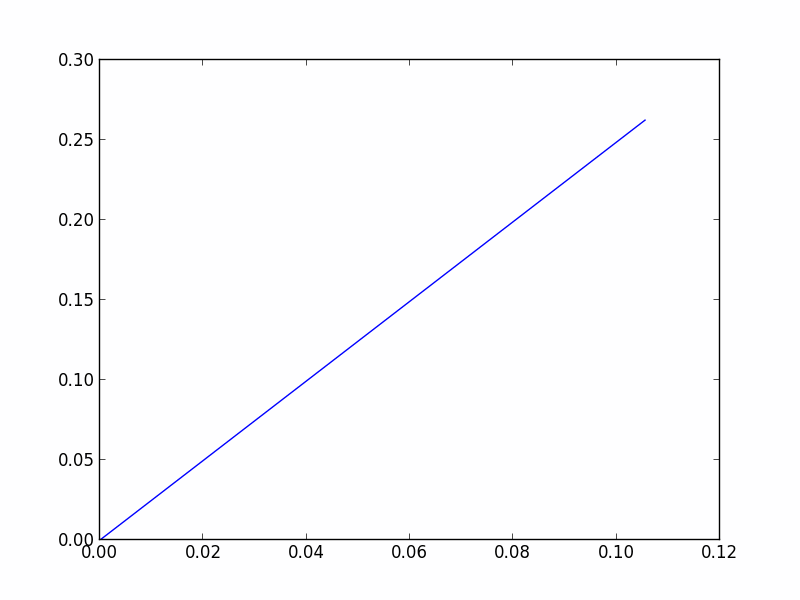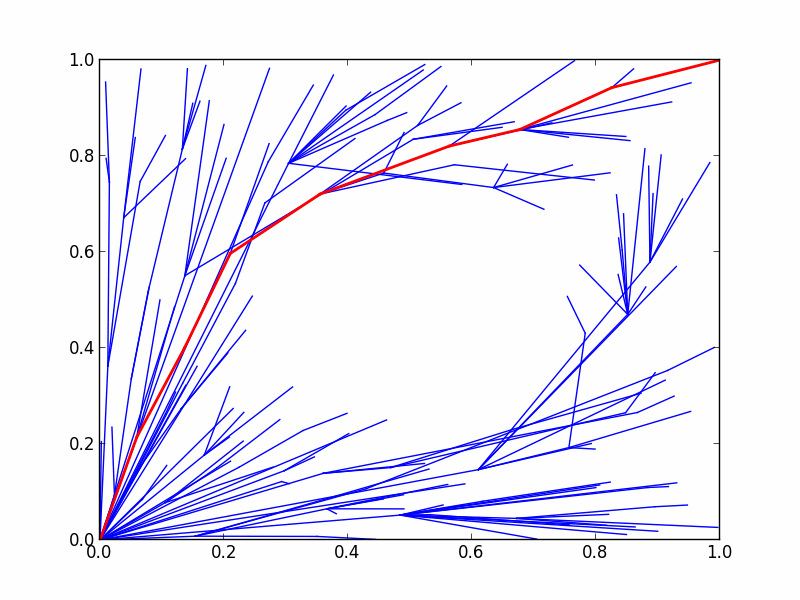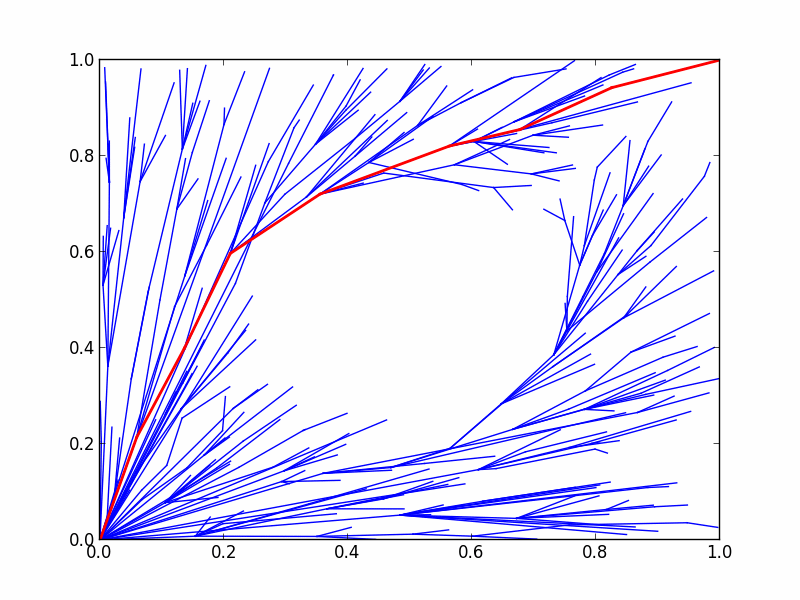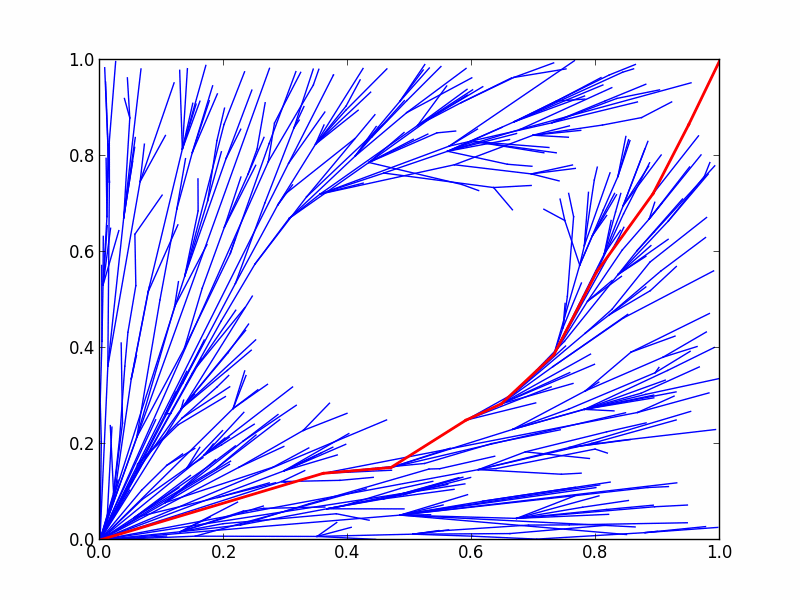
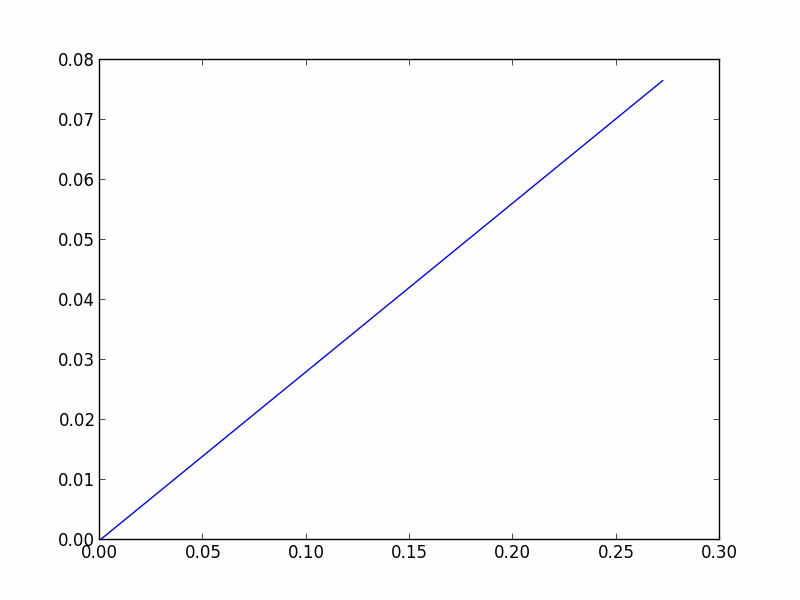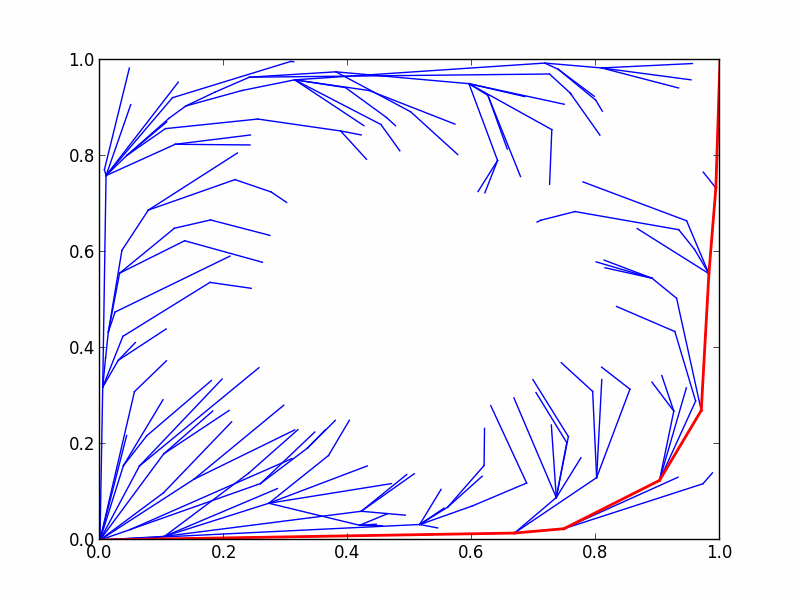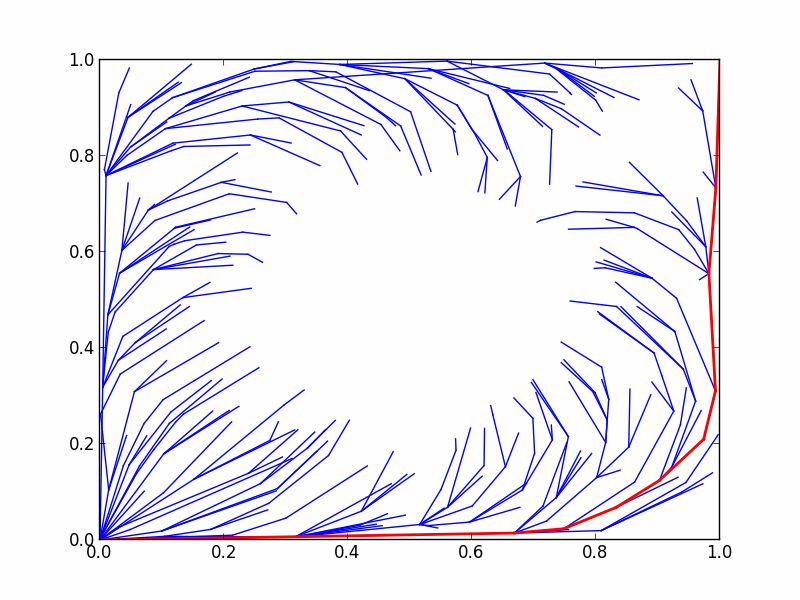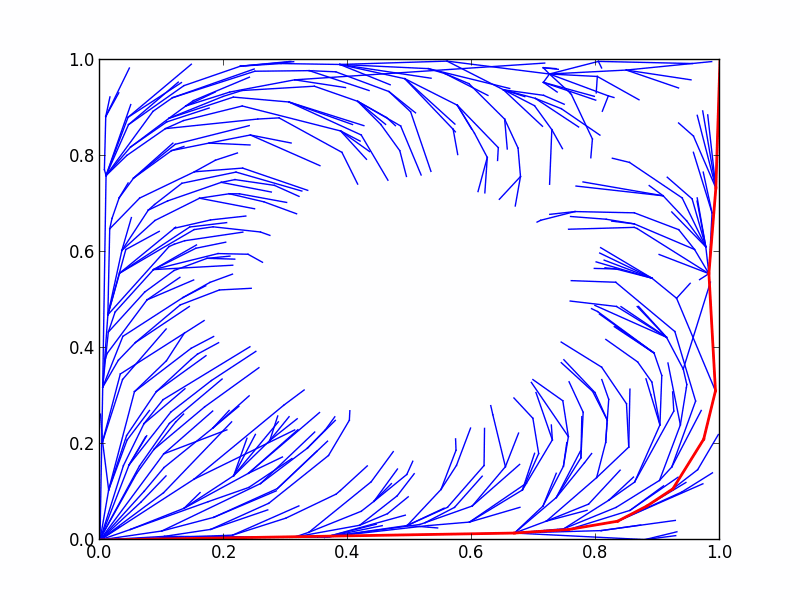
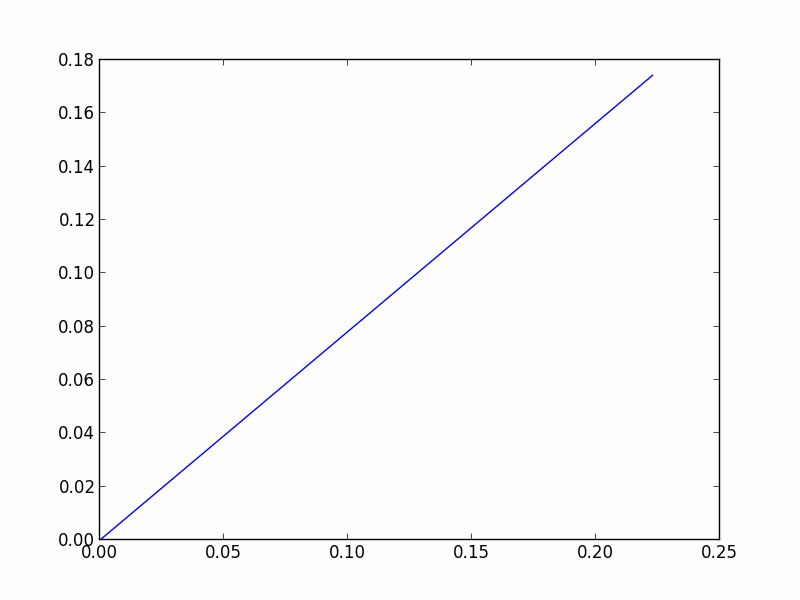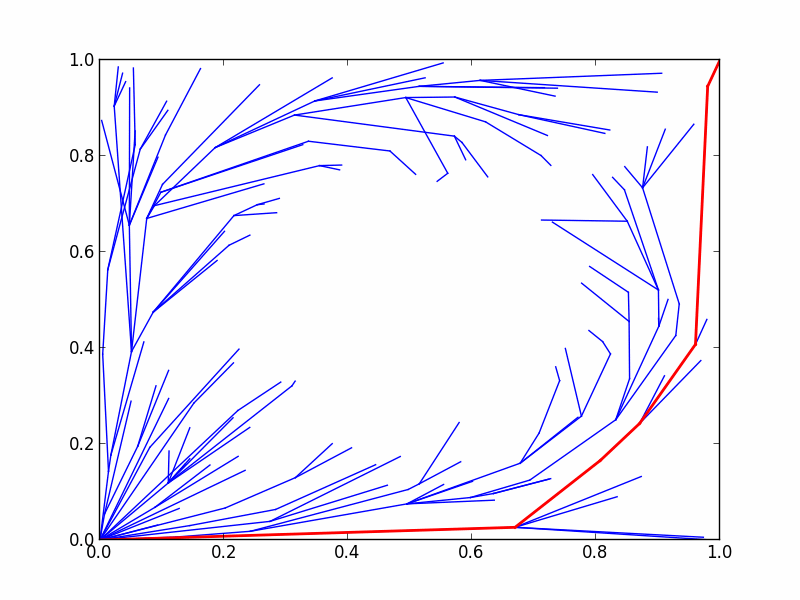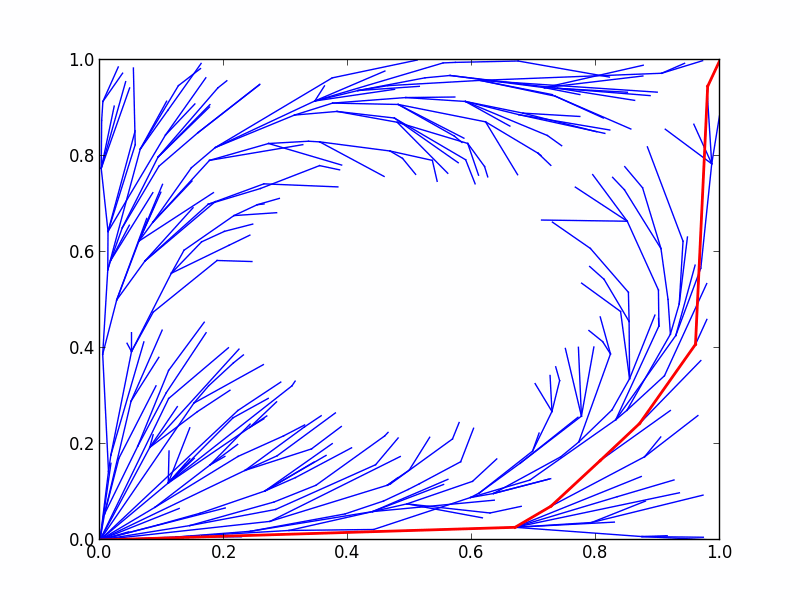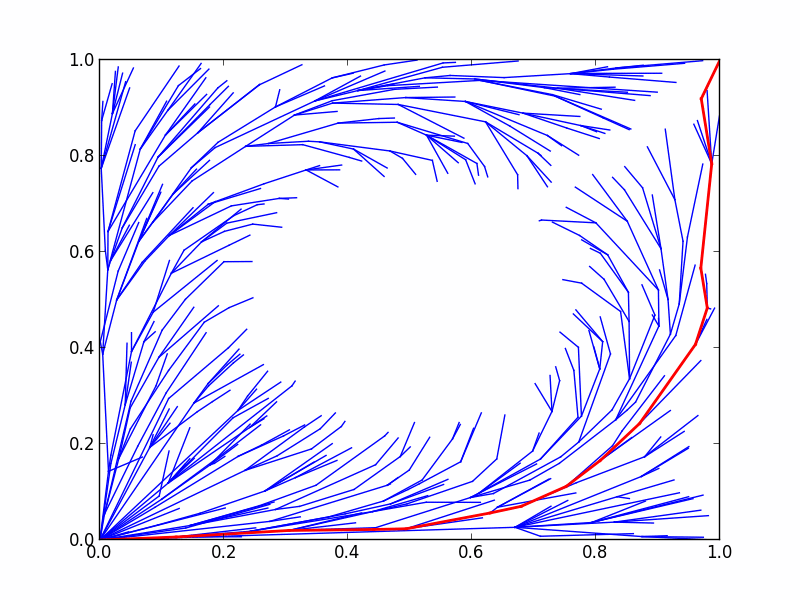
Circle Grid benchmark

。于定义的二维圆形网格问题中，用基准问题对比CForest和RRT*的性能。


8.6.4 结果

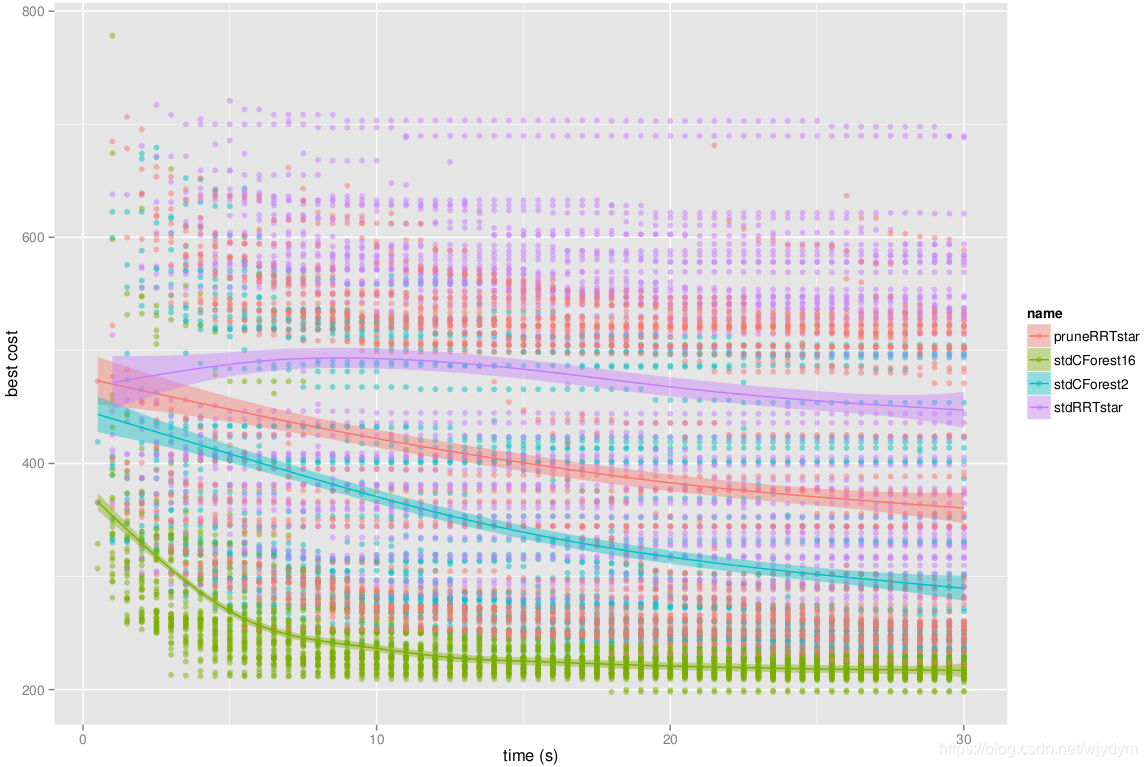
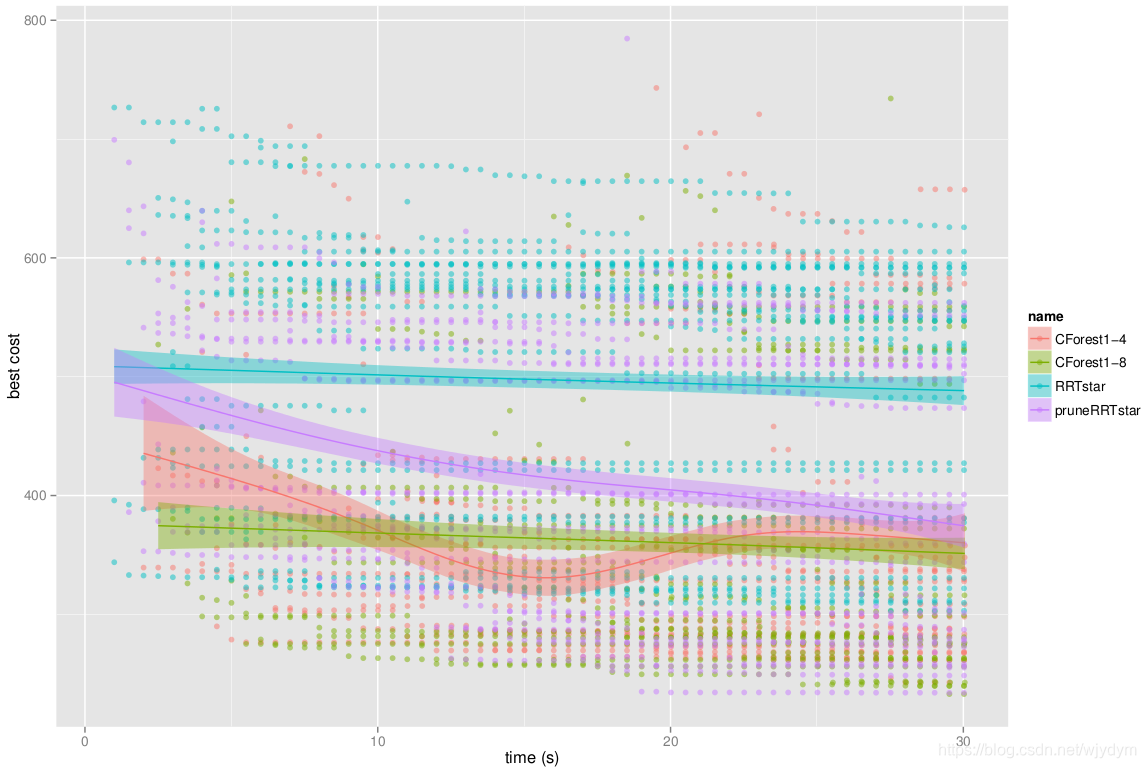
CForest 产生了很多有趣的结果。所有这些结果均通过OMPL.app中的alpha 1.5 puzzle基准配置获取 。下图展示了在16核机器中使用2和16线程运行CForest的结果。标准检查程序中还包含标准RRT*和修剪版。

图13 最佳时间消耗估计

随线程增加，CForest更快收敛至最小化消耗（最优解）。修剪的RRT*同样优于标准RRT*。

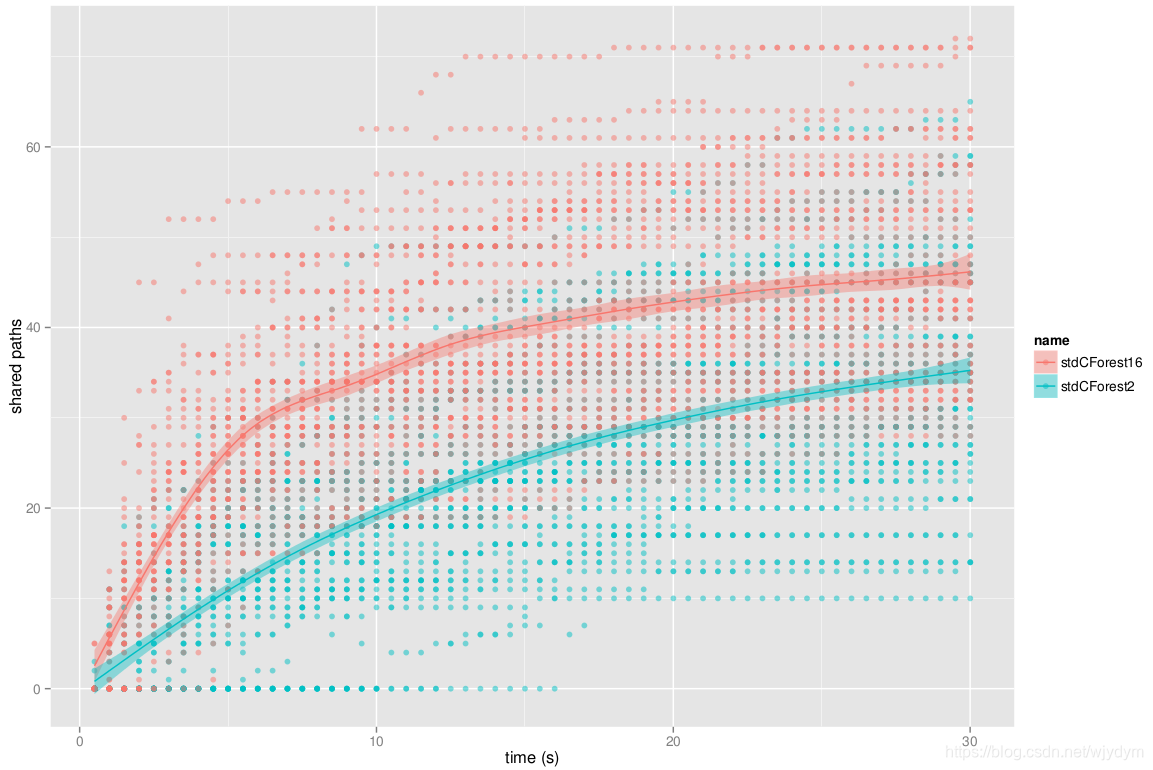
图14 CForest共享的路径数量

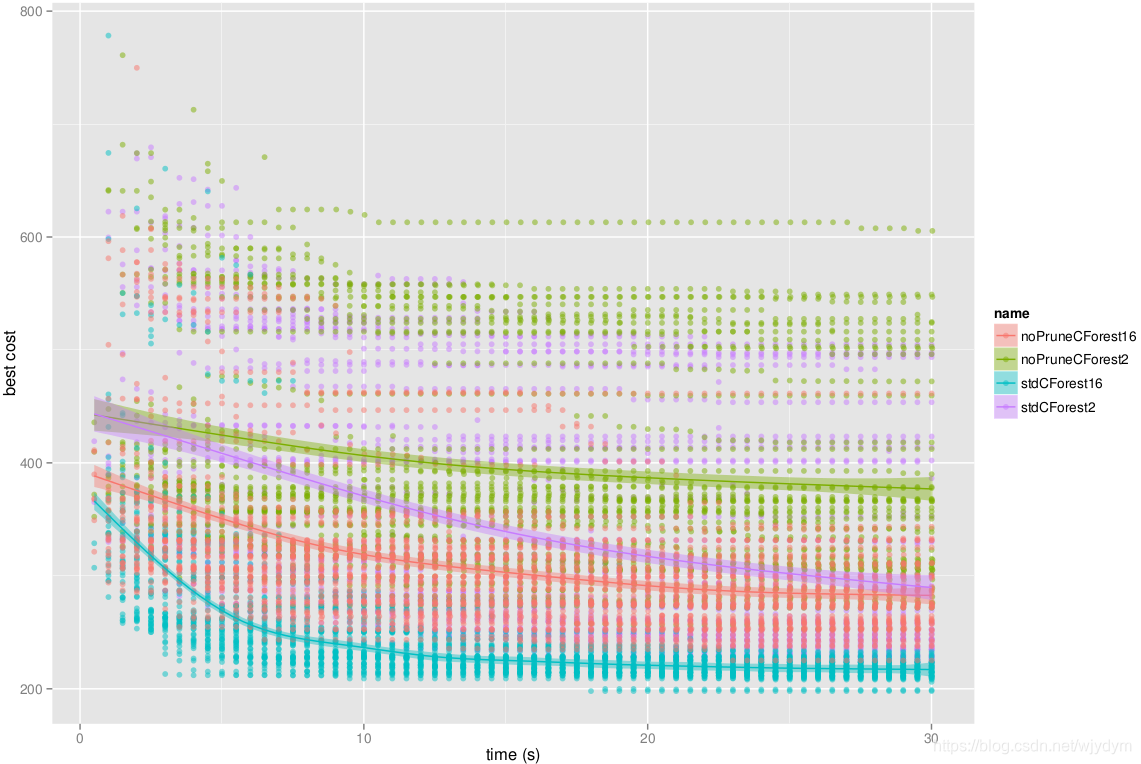
另一个有趣的实验是运行使用了无修剪的CForest，并将其与标准CForest对比。

图15 最佳时间消耗估计

无修剪的树对收敛产生了负效果。然而仍优于标准RRT*。

当仅有单核可用时，CForest仍提高了RRT*的性能。下图显示了与标准RRT*及其修剪版本比较，在单核中通过多线程使用CForest同样提升了收敛速率，在更短的时间内达到更低的消耗的解。

图16 最佳时间消耗估计

CForest的顺序版本：单核中运行多线程。


8.6.5 高级资料


8.6.5.1 设计实施的细节

CForest规划器需配合使用其自己的状态采样器

ompl::base::CForestStateSampler

和状态空间

ompl::base::CForestStateSpaceWrapper

。

ompl::geometric::CForest

囊括了此采样器及状态空间的创建，使得其对使用者完全透明开放。

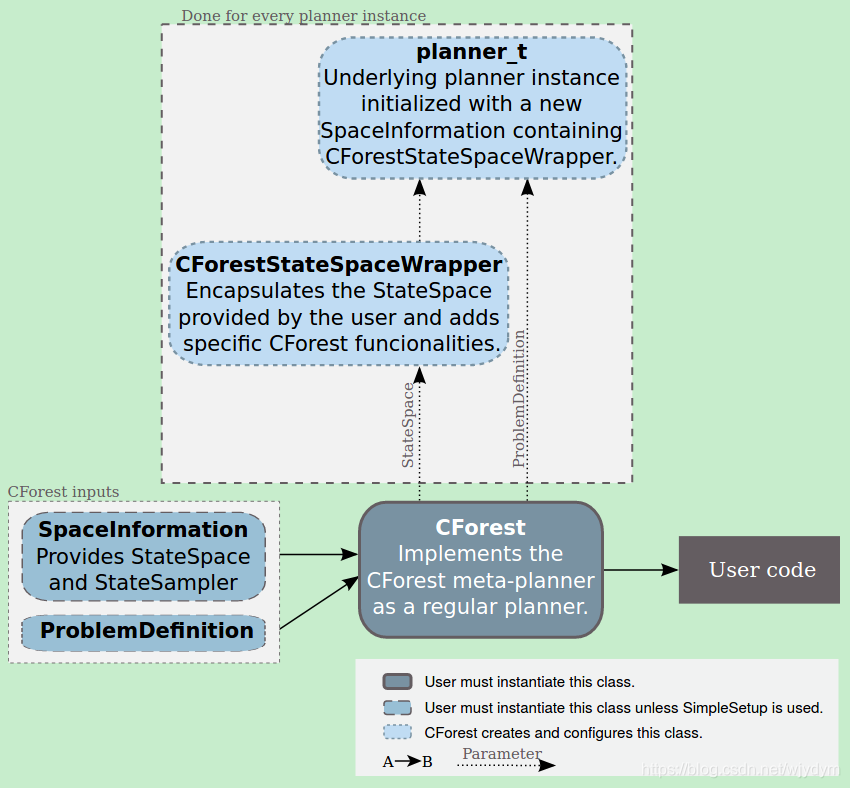
CForest作用于用户定义的

ompl::base::SpaceInformation

。但是，CForest在实例化规划器时为每个规划器创建了独立的SpaceInformation实例，包括

CForestStateSpaceWrapper的一个实例。当规划器开辟StateSampler时，CForestStateSpaceWrapper创建一个CForestStateSampler实例(为用户自定义状态采样器的封装，无自定义时为默认采样器的封装)。该设计模式总结如

下架构：

图17

设计模式说明1

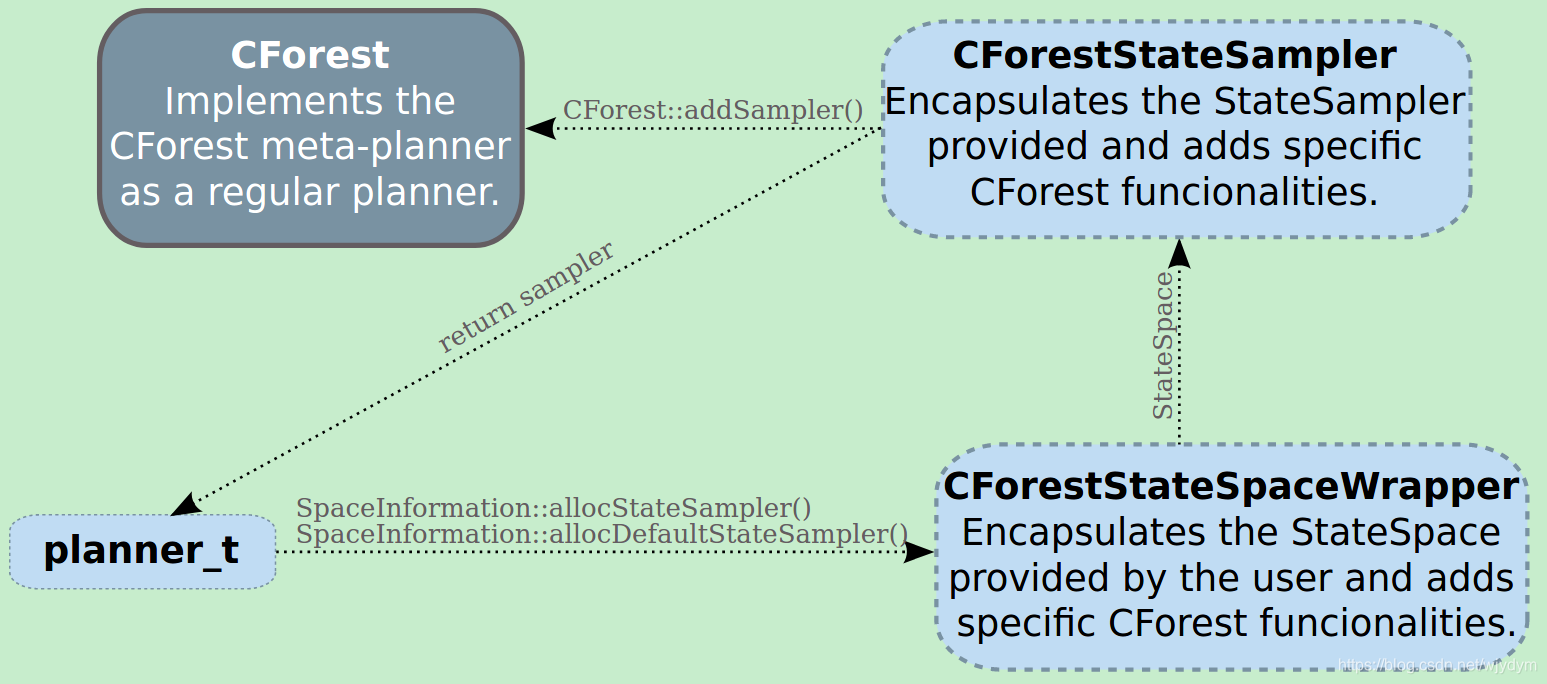
每当规划器调用

SpaceInformation::allocStateSampler()或allocDefaultStateSampler()时，CForestStateSpaceWrapper则开辟一个CForestStateSampler。

图18

设计模式说明2

因此，CForest跟踪规划器的创建，同时由于

CForestStateSpaceWrapper

，也跟踪状态采样器的创建。这使得CForest得以维护一个规划器采样器，该采样器是在树间共享路径所必须的。

该新状态采样器允许采样给定状态(与随机状态相反)。因此，当新的更好的路径被发现时，CForest将该新路径的状态点共享至所有采样器。

CForestStateSampler将采样这些状态。一旦采样状态，将根据其当前状态采样器继续采样状态。


8.6.5.2

局限性

  • CForest被设计用来解决单一查询最短规划路径问题。因此，并非支持所有

    ompl::base::OptimizationObjective

    实例。消耗度量需遵循三角不等式。注意，规划最短路径不意味着仅可优化路径长度。同样可以采用其它度量：时间，能量，等等。但是，不支持净空或平滑度的优化。
  • 一旦树被修剪，状态即被从

    NearestNeighbors数据机构中移除。但是，当前操作直到规划器实例销毁前都不会移除修剪的状态。此为规划器操作特有的，但这是计算时间最有效的方法。


8.6.5.3 使自定义规划器兼容CForest

如果你定义了一个增量的、优化的OMPL规划器，并希望使其兼容CForest，则必须对规划器实施以下3点修正：

  • CForest的激活与配置。
  • 路径共享。
  • 修剪树。


CForest的激活与配置

首先，如果使用了CForest框架，必须设置相应的共享过程解的回调机制。同时，必须包含能确认修剪是否会导致错误的检查。因此，在

solve()函数中，应添加如下代码：
 

ompl::geoemtric::MyPlanner solve(const base::PlannerTerminationCondition &ptc)
{
    // Configuration before entering the main solving loop.
    ....
    if (prune_ && !si_->getStateSpace()->isMetricSpace())
       OMPL_WARN("%s: tree pruning was activated but since the state space %s is not a metric space, the optimization objective might not satisfy the triangle inequality. You may need to disable pruning.", getName().c_str(), si_->getStateSpace()->getName().c_str());
    const base::ReportIntermediateSolutionFn intermediateSolutionCallback = pdef_->getIntermediateSolutionCallback();
    ...
    while (ptc == false) // Main loop
    ...
}


prune_

flag will be set but the user or the CForest framework. 该标志量管理与修剪树、早期状态丢弃等有关的代码。如果

intermediateSolutionCallback为false，则共享路径的代码将不被执行。

考虑到CForest的线程共享同一个

PlannerTerminationCondition，建议在solve()函数的主循环结束时紧接如下调用：
 

ompl::geoemtric::MyPlanner solve(const base::PlannerTerminationCondition &ptc)
{
    while (ptc == false) // Main loop
    {
        ...
    }
    ptc.terminate(); // Will force other threads to stop.
}

这样做在线程之一跳出循环但终止条件仍未触发时尤其有用(使其它线程均终止循环)。例如，只要设置了消耗阈值，RRTstar就会出现该情况。


注意

CForest可以不使用修剪。此情况下，

prune_标志量仅在使用true传参调用

ompl::geometricCForest::setPrune()

时被激活(默认激活)。

RRTstar中的修剪树亦可独立使用。


路径共享

CForest被设计为使用递增的、优化的规划器，需要：一个标志量，表示发现了一条新的更好的路径；一个指针，指向运动，该运动包含解的最末状态亦即目标。因此，在solve()函数主循环的最末，应添加如下所示的代码： 

ompl::geoemtric::MyPlanner solve(const base::PlannerTerminationCondition &ptc)
{
    // Configuration before entering the main solving loop.
    ...
    while (ptc == false) // Main loop
    {
        ...
        // Sampling new states.
        ...
        // Addind states to the tree.
        ...
        // Searching for improved solutions.
        ...
        if (updatedSolution)
        {
            ...
            if (intermediateSolutionCallback)
            {
                std::vector<const base::State *> spath;
                Motion *intermediate_solution = solution->parent;
                do
                {
                    spath.push_back(intermediate_solution->state);
                    intermediate_solution = intermediate_solution->parent;
                } while (intermediate_solution->parent != 0);
                intermediateSolutionCallback(this, spath, bestCost_);
            }
        } // if updated solution
    } // while ptc
}


注意

向量spath必须严格按照从目标到起点的顺序包含解的所有状态。

在该情况下，起始和目标状态不会即刻被包含进来，因为处理这两个状态较为复杂。代码简洁性占上风，但取决于用于CForest的规划器。

很有可能共享多条路径，且多个状态被修改。这意味着树和路径解将包含重复的状态。为避免该问题，在

solve()函数中紧接新状态采样的位置添加如下代码：
 

ompl::geoemtric::MyPlanner solve(const base::PlannerTerminationCondition &ptc)
{
    // Configuration before entering the main solving loop.
    ...
    while (ptc == false) // Main loop
    {
        // Sample a new state and store it in rmotion.
        ...
        // find closest state in the tree
        Motion *nmotion = nn_->nearest(rmotion);
        if (intermediateSolutionCallback && si_->equalStates(nmotion->state, rstate))
            continue;
        ...
    }
}

如果采样状态为重复的， 将予以丢弃并开始下一次迭代。


修剪树

修剪涉及两种不同的移除状态的方法：1) 修剪树上不会导向更优解的状态；2) 在向树添加前丢弃状态。两种情况下，所有修改均在solve()中重复。树中主要的修改操作：


  1. Early state rejection。

    检查随机采样是否导向更优解（使用的消耗：从起始到当前的启发式+从当前到目标的启发式）

  2. State rejection。

    大多数状态符合1的筛查，但一旦它们连接到树中后，它们无法导向更优解（使用的消耗：从起始到当前的启发式+从当前到目标的启发式）

  3. Tree pruning

    。 如果新的、更优的解被发现，修剪阈值将被减小，因此将修剪树上的状态，使得比当前最佳消耗更高消耗的状态被移除。

上述修改操作均包含在如下示例代码中： 

ompl::geometric::MyPlanner solve(const base::PlannerTerminationCondition &ptc)
{
    // Configuration before entering the main solving loop.
    ...
    while (ptc == false) // Main loop
    {
        ...
        // Sampling new states.
        ...
        sampler_->sampleUniform(rstate);
        if (prune) // Modification 1 - early state rejection
        {
            const base::Cost costTotal =  computeLowestCostToGo(rmotion);
            if (opt_->isCostBetterThan(bestCost_, costTotal))
                continue;
        }
        // Adding states to the tree.
        ...
        if (prune) // Modification 2 - state rejection.
        {
            const base::Cost costTotal = computeCostToGoal(motion);
            if (opt_->isCostBetterThan(costTotal, bestCost_))
            {
                nn_->add(motion);
                motion->parent->children.push_back(motion);
            }
            else // If the new motion does not improve the best cost it is ignored.
            {
                si_->freeState(motion->state);
                delete motion;
                continue;
            }
        }
        else // Regular code when prune is not activated.
        {
            // add motion to the tree
            nn_->add(motion);
            motion->parent->children.push_back(motion);
        }
        // Searching for improved solutions.
        ...
        if (updatedSolution)
        {
             ...
             if (prune_) // Modification 3 - tree pruning.
                 pruneTree(bestCost_);
             ...
        } // if updated solution
    } // while ptc
}

注意

应在代码中定义

pruneTree()函数。多半情况下，

RRTstar::pruneTree()直接适用。也可在无

pruneTree()方法的情况下使用

CForest。但是，强烈建议至少包含1和2两种修改方式进行状态抛弃。

完整的创建修改方法的示例请阅读

ompl::geometric::RRTstar::solve()

。

九、

Constrained Planning

（约束规划）

某些情况下，机器人的运动受任务或是其内在的运动学特性约束。比如，保持茶杯水平、与某表面保持接触以进行书写、遵循空间中某曲线以响应任务需求。

与非约束规划基本类似，主要区别是约束的定义、约束状态空间(环绕在外围状态空间)的使用。

约束满足子流形
X = \{ q \in \mathcal{Q} \mid f(q) = \mathbf{0} \}
，将机器人状态空间
\mathcal{Q}
映射到实际向量空间
\mathbb{R}^n
，因此定义约束实际上就是定义
f(q)
，满足约束就是满足
f(q) = \mathbf{0}
，满足约束的运动就是沿路径各点均满足
f(q) = \mathbf{0}
。比如，欲保持茶杯水平，可将茶杯的轴线与竖直Z轴的角距定义为约束方程。

约束的存在允许基于采样的规划器(包括asymptotically optimal planners)在约束条件下规划，同时仍可以避障以及实现其它优化目标。

下面将围绕示例展开特性说明。该示例定义了一个简单的约束规划问题：一个
\mathbb{R}^3
空间中的点被约束至一个球的表面，约束方程是
f(q) = \lVert q \rVert - 1
。该示例大致类似例子

ConstrainedPlanningSphere

。

9.1 定义约束(利用该约束定义受约束状态空间)

除以下预定义约束外还可进行自定义约束。

其中


ompl::base::ConstraintIntersection

可

组合多个约束

。

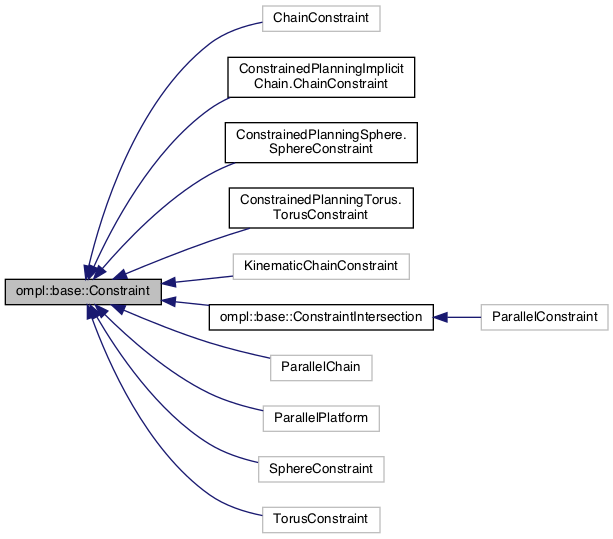
图19

预定义约束

自定义约束应继承自


ompl::base::Constraint

，其中

ompl::base::Constraint::function()

必须被定义，而解析雅克比非必须。构造函数的第二个参数是约束本身的自由度，而不是约束后状态的自由度。
 

// Constraints must inherit from the constraint base class. By default, a
// numerical approximation to the Jacobian of the constraint function is computed
// using a central finite difference.
class Sphere : public ob::Constraint
{
public:
    // ob::Constraint's constructor takes in two parameters, the dimension of
    // the ambient state space, and the dimension of the real vector space the
    // constraint maps into. For our sphere example, as we are planning in R^3, the
    // dimension of the ambient space is 3, and as our constraint outputs one real
    // value the second parameter is one (this is also the co-dimension of the
    // constraint manifold).
    Sphere() : ob::Constraint(3, 1)
    {
    }
    // Here we define the actual constraint function, which takes in some state "x"
    // (from the ambient space) and sets the values of "out" to the result of the
    // constraint function. Note that we are implementing `function` which has this
    // function signature, not the one that takes in ompl::base::State.
    void function(const Eigen::Ref<const Eigen::VectorXd> &x, Eigen::Ref<Eigen::VectorXd> out) const override
    {
        // The function that defines a sphere is f(q) = || q || - 1, as discussed
        // above. Eigen makes this easy to express:
        out[0] = x.norm() - 1;
    }
};

通过约束方程定义了一个
\mathbb{R}^3
空间中的球形：

图20 自定义约束体示意


9.1.1



Constraint



成员函数：约束雅克比jacobian（可选项，提高约束规划问题的运算效率，尤其是高维空间）

该解析雅克比可通过手算，也可通过


ConstraintGeneration.py



使用符号解算器

获得(

使用


SymPy

），总之为约束类添加以下函数以计算雅克比。如果未定义，则默认为 a numerical finite central difference routine以近似实现雅克比，这是密集运算，所以最好还是提供一个解析雅克比。 

// Implement the Jacobian of the constraint function. The Jacobian for the
// constraint function is an matrix of dimension equal to the co-dimension of the
// constraint by the ambient dimension (in this case, 1 by 3). Similar to
// `function` above, we implement the `jacobian` method with the following
// function signature.
void Sphere::jacobian(const Eigen::Ref<const Eigen::VectorXd> &x, Eigen::Ref<Eigen::MatrixXd> out) const override
{
    out = x.transpose().normalized();
}


9.1.2



Constraint



成员函数project

约束的其中一个基本特性就是映射方程


ompl::base::Constraint::project()

。该函数将输入看做可能不满足约束的状态并将其映射到约束子流形，生成一个满足约束的状态。该函数

默认使用的牛顿法在多数情形下效果良好。该函数可按照你自己的映射规则进行重写。比如在该球形示例中，可以将状态归一化以映射到球面上，再比如复杂机械臂的逆运动学。

  • 生成当前状态的雅克比；
  • 利用雅克比更新状态；
  • 将状态代入


    function()

    验证其是否满足约束。

重复以上步骤直到生成满足约束的状态。该函数为虚函数，可按需求重写，如逆运动学。


9.1.3 参数



ompl::base::Constraint

的性能受两个参数的影响。



a)


tolerance

：

表征偏离约束的容忍度，容忍度要求低则易获得规划结果。

tolerance被用于

ompl::base::Constraint::project()

和

ompl::base::Constraint::isSatisfied()

以判定状态满足约束。对于能承受宽容忍度的规划问题(如高顺应机器人)，应放宽容忍度。这通常将简化规划问题，因为约束更容易被满足。

可通过成员函数


setTolerance()

或

构造函数Constraint( )设置。如果使用的是构造函数： 

...
    // Set ambient and constraint dimension, along with tolerance (1e-3, in this case).
    Sphere() : ob::Constraint(3, 1, 1e-3)
...



b)

maxIterations

：


maxIterations被用于限制映射规则的迭代使用次数，当无法找到满足约束的构型时。当约束方程特别弱时应减小迭代次数，


反之特别强时，应增大迭代次数。通过成员函数

setMaxIterations()

设置。


9.2 定义约束状态空间


9.2.1 外围状态空间

定义约束状态空间前须先定义外围状态空间，此处为
\mathbb{R}^3
空间。 

// Create the ambient space state space for the problem.
auto rvss = std::make_shared<ob::RealVectorStateSpace>(3);
// Set bounds on the space.
ob::RealVectorBounds bounds(3);
bounds.setLow(-2);
bounds.setHigh(2);
rvss->setBounds(bounds);


9.2.2 实例化约束

约束实例将被用以创建约束状态空间。 

// Create our sphere constraint.
auto constraint = std::make_shared<Sphere>();


9.2.3

约束状态空间

及

约束状态空间信息

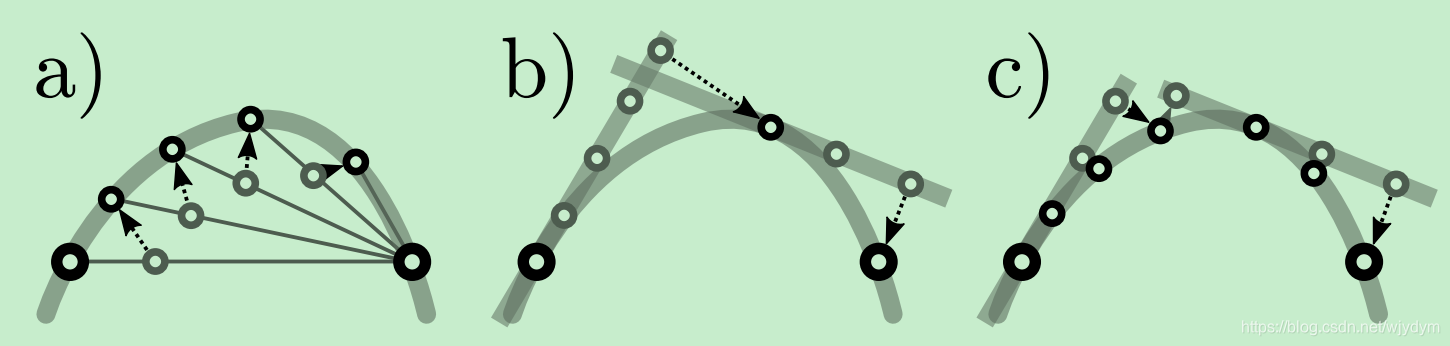
如图，存在3种预定义的受约束状态空间(继承自


ompl::base::ConstrainedStateSpace


)，其对子流形的采样和遍历方式与普通状态空间不同。

a)


Projected

 		b)


Atlas

 		c)


TangentBundle
图21 三种预定义约束状态空间的修正示意

另外约束状态空间

须对应使用



ob::ConstrainedSpaceInformation

。OMPL采用的约束空间实现方法见

论文

（约束运动规划详述见

论文

）。

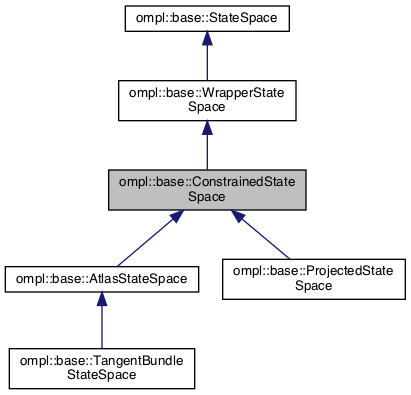
图22 预定义的约束状态空间

依靠前述定义的约束和外围状态空间，可以进一步定义约束状态空间。针对此例，我们将使

用

ompl::base::ProjectedStateSpace

，

其采用了projection operator-based methodology以满足约束。此处也可以使用


ompl::base::AtlasStateSpace

或

ompl::base::TangentBundleStateSpace

。


对应的，我们创建

ompl::base::ConstrainedSpaceInformation

，

它是在


ompl::base::SpaceInformation

的基础上增加了一点修饰以纳入约束。
 

// Combine the ambient space and the constraint into a constrained state space.
auto css = std::make_shared<ob::ProjectedStateSpace>(rvss, constraint);
// Define the constrained space information for this constrained state space.
auto csi = std::make_shared<ob::ConstrainedSpaceInformation>(css);



ompl::base::ConstrainedSpaceInformation

做的最重要的事之一为调用

ompl::base::ConstrainedStateSpace::setSpaceInformation

，允许遍历流形进行碰撞检测及离散测量计算。

9.3

内在限制

为确保约束规划正常工作，约束状态空间的基础状态空间和约束方程须满足以下假定。


9.3.1 连续内存

状态空间的内存分配是连续的double值，确保了可被视为

Eigen::VectorXd

。组合空间


CompoundStateSpace



无法应用于约束规划

，因其各子状态空间之间的内存不连续。


9.3.2 约束方程可微

约束方程应连续且可微，否则奇点将引发错误。


AtlasStateSpace

与

TangentBundleStateSpace

将奇点视为障碍物。


9.3.3 必须插值

满足约束的路径通常需经过插值才能被真实系统执行，无论简化或未简化的. 调

用

og::PathGeometric::interpolate()

即可，插值过的路径满足约束条件。由于插值可能失败，因此该步骤可能出错。


9.3.4 插值失败

插值的距离增量”delta”由


ob::ConstrainedStateSpace::setDelta()

设置决定。插值失败可能是因为约束中的奇点、约束子流形的高曲率以及很多其它方面的原因。非约束状态空间(如

RealVectorStateSpace

)因其解析性通常不会插值失败，因此作出插值永远不会失败的假定。而这种假定会在约束空间下插值失败时引起不可预见的问题。增大或减小

ConstrainedStateSpace


的”delta”或其偏离约束容忍度“tolerance”，以及调整其它超参数将修复这些问题。


9.3.5 超参数敏感性

约束状态空间通常对其一众超参数的调整较为敏感。虽已为超参数分配了合理的默认值，但面对众多约束规划问题，不同特性的约束子流形需对应设置不同的参数值。一些基本的经验法则如下：

  • For high-dimensional ambient state spaces, many parameters can be increased in magnitude. A brief non-exhaustive list follows.（基础状态空间维度增加，参数值应相应增大）

  • Generally, the step size for manifold traversal is related to the relative

    curvature

    of the underlying constraint submanifold. Less curvy submanifolds can permit larger step sizes (i.e., if the constraint defines a hyperplane, you can use a large step size). Play around with this value if speed is a concern, as the larger the step size is, the less time is spent traversing the manifold.（随曲率减小可增大步进距离，以缩短遍历时间）
  • For the atlas- and tangent bundle-based spaces, planners that rely on uniform sampling of the space may require a high exploration parameter so the constraint submanifold becomes covered quicker (e.g., BIT*). Additionally, planners that rely on

    ompl::base::StateSampler::samplerNear()

    may also require a high exploration or ρ parameter in order to expand effectively.（对于atlas和tangent两种约束空间，使用uniform sampling的规划器需要更大的参数以更快遍历。使用

    samplerNear()的规划器同样需要大参数值或者大

    ρ。）
  • And many others! In general, the projection-based space is less sensitive to poor parameter tuning than atlas- or tangent bundle-based space, and as such is a good starting point to validate whether a constrained planning problem is feasible.（projection-based约束空间对参数变化不敏感，可用来检测约束规划问题的可行性。）

9.4 Constraint Projection 对比

Projection Evaluator

在9.1.2中提到


Constraint

的成员函数

project()

。而2.3中提到的

ompl::base::ProjectionEvaluator

同样含有project()函数。被少数规划器用以估计覆盖范围，原理同样是对空间进行降维(但与constraint成员函数不同的是使用了正交概念)。可以使用一些采用了

ProjectionEvaluator

的规划器(例如

KPIECE1

、

ProjEST

、


SBL

等等

）完成约束规划任务。与2.3中一样，需要确保规划器能通过相同的命名找到状态空间中对应的

ProjectionEvaluator


。若使用了

ConstrainedProblem

，可以使用其成员函数setPlanner()在以规划器枚举类型名创建规划器时为其注册ProjectionEvaluator(本质与2.3一样，也是使用了规划器的setProjectionEvaluator()函数)： 

 bool spherePlanningOnce(ConstrainedProblem &cp, enum PLANNER_TYPE planner, bool output)
 {
     cp.setPlanner(planner, "myProjection");
     ……
 }

默认情况下，约束状态空间将使用


WrapperProjectionEvaluator

调用基础状态空间的默认

projection evaluator。当了解规划问题的空间结构时，可以自定义projection evaluator，

<球面示例>

。示例中使用了球面极坐标完成了降维，可以这么理解，

Projection Evaluator

为规划器提供了一个符合约束的状态，这样


Constraint

的成员函数

project()

拥有一个满足约束条件的输入，不用进行迭代。若使用了默认的


Projection Evaluator

，其输出未经处理，需要依靠迭代来生成符合约束的状态。因此若对约束能给出一个准确的降维描述，那么自定义一个

Projection Evaluator

，并重写其project()，这种直接获得符合约束的状态的方法要比迭代更节省运算。

9.5 定义求解问题

此处将规划问题定为沿球面从南极到北极，并躲避赤道上的障碍。定义约束条件下的求解问题与非约束条件下基本一致，使用一系列相同的工具。


9.5.1 SimpleSetup(



ompl::geometric::SimpleSetup



)
 

// Simple Setup
auto ss = std::make_shared<og::SimpleSetup>(csi);


9.5.2 状态评估器

此处为简单的开口带状障碍。 

bool obstacle(const ob::State *state)
{
    // As ob::ConstrainedStateSpace::StateType inherits from
    // Eigen::Map<Eigen::VectorXd>, we can grab a reference to it for some easier
    // state access.
    const Eigen::Map<Eigen::VectorXd> &x = *state->as<ob::ConstrainedStateSpace::StateType>();
    // Alternatively, we could access the underlying real vector state with the
    // following incantation:
    //   auto x = state->as<ob::ConstrainedStateSpace::StateType>()->getState()->as<ob::RealVectorStateSpace::StateType>();
    // Note the use of "getState()" on the constrained state. This accesss the
    // underlying state that was allocated by the ambient state space.
    // Define a narrow band obstacle with a small hole on one side.
    if (-0.1 < x[2] && x[2] < 0.1)
    {
        if (-0.05 < x[0] && x[0] < 0.05)
            return x[1] < 0;
        return false;
    }
    return true;
}
// Set the state validity checker in simple setup.
ss->setStateValidityChecker(obstacle);
图23 添加障碍后的约束状态空间


9.5.3 起点状态、终点状态设置

确保设置的状态

符合约束方程

，否则将引发错误。此处按要求设置为南极和北极。 

// Start and goal vectors.
Eigen::VectorXd sv(3), gv(3);
sv << 0, 0, -1;
gv << 0, 0,  1;
// Scoped states that we will add to simple setup.
ob::ScopedState<> start(css);
ob::ScopedState<> goal(css);
// Copy the values from the vectors into the start and goal states.
start->as<ob::ConstrainedStateSpace::StateType>()->copy(sv);
goal->as<ob::ConstrainedStateSpace::StateType>()->copy(gv);
// If we were using an Atlas or TangentBundleStateSpace, we would also have to anchor these states to charts:
//   css->anchorChart(start.get());
//   css->anchorChart(goal.get());
// Which gives a starting point for the atlas to grow.
ss->setStartAndGoalStates(start, goal);


9.5.4 规划器

选取规划器，


ompl::geometric

命名空间内，此处选择

ompl::geometric::PRM

。
 

auto pp = std::make_shared<og::PRM>(csi);
ss->setPlanner(pp);


9.5.5 求解

各项点已就位，最后配置求解环境。 

ss->setup();

同定义求解问题一样，求解过程与非约束问题基本一致。此处给予规划器5s的规划时间。 

// Solve a problem like normal, for 5 seconds.
ob::PlannerStatus stat = ss->solve(5.);
if (stat)
{
    // Path simplification also works when using a constrained state space!
    ss->simplifySolution(5.);
    // Get solution path.
    auto path = ss->getSolutionPath();
    // Interpolation also works on constrained state spaces, and is generally required.
    path.interpolate();
    // Then do whatever you want with the path, like normal!
}
else
    OMPL_WARN("No solution found!");


9.5.6 插值

直接求解得到的路径点通常较为稀疏，经过优化的路径更甚。欲获得较为密集，且符合约束条件的中间路径点时，需对路径进行插值。使用函数


ompl::geometric::PathGeometric::interpolate()

。

9.6

总结

上述使用PRM的规划结果如下图所示，黄色高亮线为简化路径。

简言之，区别于普通状态空间的部分为定义约束方程、定义外围空间、定义约束状态空间。

图24 结果示意

9.7

更多约束规划示例


文章

中提到的约束规划问题被编写为示例程序，见

ompl/demos/constraint

文件夹。这些示例融入了benchmarking，并能方便地配置约束空间的各超参数。并将规划结果以3D形式

Blender

文件展现，文件路径

ompl/demos/constraint/visualization。更多示例的

详细说明见

。

十、

使用ODESolver以实现含控制的规划

OMPL提供了一个

boost::numeric::odeint

包的封装类用于数值化求解微分方程。虽然存在其它的软件包(如GSL, ALGLIB, Scipy)可进行数值积分，但是odeint库功能多样、易于使用且外部依赖较少。

ODESolver类特别适于运动规划问题。它为使用者提供一个对象，能够求解具有
\dot{q} = f(q,u)
形式的方程，其中
q
代表当前系统状态，
u
代表状态
q
下用于系统的控制。ODESolver的使用可以方便使用者不必在其代码中操作数值积分，并且允许高级用户自定义积分方法。

10.1 理论基础

假设规划一个简化的类汽车系统问题，速度
v
和转向角
\phi
可直接控制。汽车的位姿可表示为(x,y,
\theta
)。则其位姿微分可表示为：

\left( \begin{array}{c} \dot{x}\\ \dot{y}\\ \dot{\theta} \end{array} \right) = \left( \begin{array}{c} v \cos(\theta)\\ v \sin(\theta)\\ v \tan(\phi) \end{array} \right)

这表明了一个给定的汽车状态(x,y,
\theta
)将如何随单一控制(
v, \phi
)变化。上式中左边为当前状态的微分，亦即该式求取的是状态值的微分而不是新状态本身。因此，当在给定时间段内实施控制后，该方程必须经过积分才能获取新状态。

对大多数非线性微分方程而言，难以计算其精确解。通过将时间离散化为小增量，在每段增量内重新估计系统，可求取方程近似解。然而该离散化操作将引入计算误差。较小的步长引入的误差小，但是计算时间长，因为迭代次数增加。 不关注各数值方法求取近似解的具体方式， 一言以蔽之，数值方法的阶次决定了解的精度，阶数高精度忧。例如，典型的

欧拉积分

为1阶，表明每次时间步长迭代的误差为
O(t^2)
，而全局误差为
O(t)
，其中
t
时间步长的大小。更多关于常微分方程数值积分理论的详细探讨见

Wikipedia

。

10.2 OMPL中ODESolver的使用

使用ODESolver前，须先定义描述系统ODE的函数。该函数必须按照如下形式： 

namespace oc = ompl::control;

void ODE(const oc::ODESolver::StateType& q, const oc::Control* u, oc::ODESolver::StateType& qdot)

向量
q
(StateType的数据类型为std::vector)表示系统当前状态，控制
u
表示向系统当前状态施加的输入，向量qdot用于存储计算输出。ODESolver使用

boost::numeric::odeint

计算数值积分，因此必须将状态值

ompl::base::State

转化为实值的可迭代容器
q
。
q
类似于调用

ompl::base::ScopedState::reals

获取的值。

10.3 定义ODE

假设规划问题为10.1中描述的类汽车系统。汽车的状态空间是

SE(2)

(位置x、y，以及方向角)，直接使用OMPL中预定义的状态空间

ompl::base::SE2StateSpace

。该系统的控制

ompl::control::ControlSpace

包含速度和转向角。根据以上分析，ODESolver的ODE可定义为： 

namespace oc = ompl::control;
void SimpleCarODE(const oc::ODESolver::StateType& q, const oc::Control* c, oc::ODESolver::StateType& qdot)
{
    // Retrieve control values.  Velocity is the first entry, steering angle is second.
    const double *u = c->as<ompl::control::RealVectorControlSpace::ControlType>()->values;
    const double velocity = u[0];
    const double steeringAngle = u[1];
    // Retrieve the current orientation of the car.  The memory for ompl::base::SE2StateSpace is mapped as:
    // 0: x
    // 1: y
    // 2: theta
    const double theta = q[2];
    // Ensure qdot is the same size as q.  Zero out all values.
    qdot.resize(q.size(), 0);
    qdot[0] = velocity * cos(theta);            // x-dot
    qdot[1] = velocity * sin(theta);            // y-dot
    qdot[2] = velocity * tan(steeringAngle);    // theta-dot
}

10.4 基本示例

使用ODESolver规划时，使用者必须实例化派生求解器。所有求解器的构造函数均需要当前状态空间信息类的智能指针SpaceInformationPtr，用于从

ompl::base::State

中提取值到容器中用于状态空间积分。ODE也应传入构造函数。最简单的求解器为

ompl::control::ODEBasicSolver

，使用四阶

龙格-库塔

积分。以上述汽车问题和定义的ODE为例，求解器使用如下代码片段初始化：

注：以下提及的SpaceInformation均为

ompl::control::SpaceInformation

，不是ompl::base::Spaceinformation。 

// SpaceInformationPtr is defined as the variable si.
ompl::control::ODESolverPtr odeSolver (new ompl::control::ODEBasicSolver<> (si, &SimpleCarODE));

基于控制的规划器还需要

ompl::control::StatePropagator

对象，用以定义系统在给定控制下如何运动。ODESolver通过静态函数

ompl::control::ODESolver::getStatePropagator

为该需求提供了封装。 

si->setStatePropagator(ompl::control::ODESolver::getStatePropagator(odeSolver));

以上为所有必须项，通过求解定义于ode中的微分方程，规划器对控制采样并使其作用于系统。某些系统中，post-numerical integration回调事件很有用。例如，ODE允许状态无限制地变化，但是一些系统并不允许这样的行为。在前述的汽车问题中，方向角
\theta
取值范围为[0,
2\pi
]，而积分结果可能越过该界限。在这样的情况下，定义一个于数值积分完成后触发的post-numerical integration回调事件将很有用： 

void postPropagate(const base::State* state, const Control* control, const double duration, base::State* result)
{
    ompl::base::SO2StateSpace SO2;
    // Ensure that the car's resulting orientation lies between 0 and 2*pi.
    ompl::base::SE2StateSpace::StateType& s = *result->as<ompl::base::SE2StateSpace::StateType>();
    SO2.enforceBounds(s[1]);
}

关于ODESolver和postPropagate方法还有一个注意点。如果系统中某些状态空间元素不经ODE操作改变(比如the current gear of a car’s transmission)，这些元素的值须显式地拷贝至结果状态。ODESolver将只更新状态空间的实值。含有未经实值化处理的元素的状态空间，post-integration回调事件可被用来由初始状态向结果状态传递信息。

一旦postPropagate方法已被定义，每一个状态被传播后，将通过函数指针自动调用postPropagate方法创建StatePropagator。 

si->setStatePropagator(ompl::control::ODESolver::getStatePropagator(odeSolver, &postPropagate));

10.5 选择一个

ODESolver

存在三个预定义的派生ODESolver，使用

boost::numeric::odeint

求解系统的常微分方程。作为类模板，它们均使用了一个表示相应数值积分方法的默认模板参数。


  • ompl::control::ODEBasicSolver

    。一种简单的显式ODE求解器。默认模板参数为4阶龙格-库塔积分。该求解器为boost::numeric::odeint中基本步进器概念的封装。

  • ompl::control::ODEErrorSolver

    。一种可补偿估计误差的显式求解器。默认模板参数为5阶Runge-Kutta Cash-Karp算法，其误差范围为4阶。该求解器为boost::numeric::odeint中误差步进器概念的封装。

  • ompl::control::ODEAdaptiveSolver

    。一种显式求解器，使用自适应时间步长以将估计误差控制在给定范围内。默认模板参数为5阶Runge-Kutta Cash-Karp算法，其误差范围为4阶，配合boost::numeric::odeint的受控Runge-Kutta步进器。该求解器必须支持boost::numeric::odeint的误差步进器概念。

图25 预定义的ODESolver

选择求解器以求解系统更像是一门艺术，它取决于一系列因素，例如方程的复杂度、估计方程结果的消耗。高阶方法更精确且更数值稳定，但是带来更高的计算消耗。


ompl::control::ODESolver

基类可用于新的用户自定义求解器。ODESolver基类不依赖于boost::numeric::odeint，用户可自己编写代码或使用第三方库实现数值积分。


版权声明：本文为wjydym原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。