重点
- B树的基本特点
- B树的建立、插入和删除操作
- B+树的基本概念
1. B树及其基本操作
1.1 概念
B树又称多路平衡查找树,B树中所有节点的孩子个数的最大值称为B树的阶m。
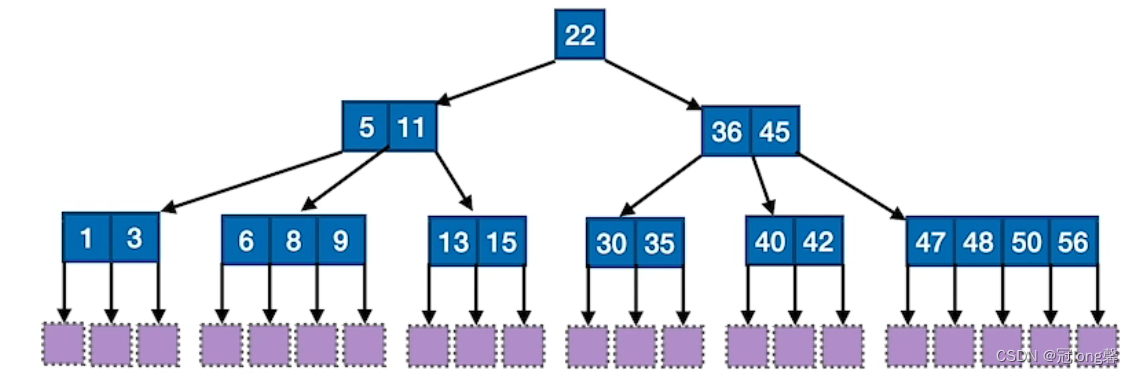
(1)性质
一棵m阶B树或为空树,或为满足一下特性的m叉树:
- 对任一节点,其所有子树高度相同。
-
根节点的子树数∈[2,m],关键字数∈[1,m-1]。其他节点的子树数∈[[m/2],m],关键字数∈[[m-2]-1,m-1]
。 -
所有非叶节点的结构如下:
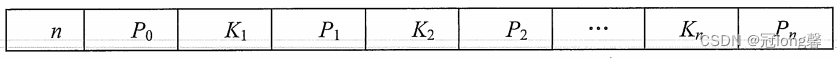
其关键字值满足子树0<关键字1<子树1<关键字2…。
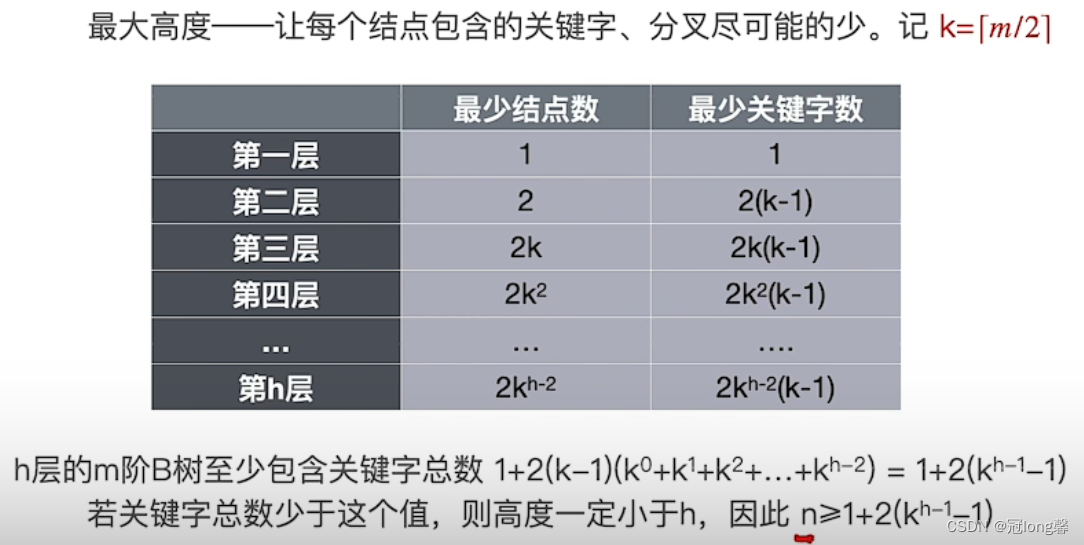
(2)高度
-
最小高度
:
h≥
log
m
(
n
+
1
)
h \geq \log_m(n+1)
h
≥
lo
g
m
(
n
+
1
)
让每个节点尽可能满,有m-1个关键字,m个分叉。即有
n≤
(
m
−
1
)
(
1
+
m
+
m
2
+
⋯
+
m
h
−
1
)
=
m
h
−
1
n \leq (m-1)(1+m+m^2+\cdots+m^{h-1})=m^h-1
n
≤
(
m
−
1
)
(
1
+
m
+
m
2
+
⋯
+
m
h
−
1
)
=
m
h
−
1
,因此
h≥
log
m
(
n
+
1
)
h \geq \log_m(n+1)
h
≥
lo
g
m
(
n
+
1
)
。
-
最大高度
:
h≤
log
[
m
/
2
]
(
n
+
1
2
)
+
1
h \leq \log_{[m/2]}(\frac{n+1}{2})+1
h
≤
lo
g
[
m
/
2
]
(
2
n
+
1
)
+
1
1.2 基本操作
(1)B树的查找
B树上的每一个结点都是有多个关键字的有序表。
-
在B树上找结点
-
在结点内找关键字
:现在有序表中查找,若没有找到则按照指针信息到子树中查找。查找到叶节点时,说明树中没有对应关键字,查找失败。
(2)B树的插入
核心要求:
-
对于m阶B树,除根节点外,结点关键字个数[m/2]-1
≤\leq
≤
n
≤\leq
≤
m-1。 - 子树0<关键字1<子树1<关键字2…
思路
-
定位
:
新元素一定插入到最底层的“终端节点“
,用查找确定插入位置。 -
分裂
:若原节点关键字数超过上限,则
从中间位置[m/2]将其中的关键字分为两部分。左部分包含的关键字放在原节点中,右部分包含的关键字放在新结点中,中间位置插入原节点的父节点
。若导致父节点的关键字个数也超过上限,则继续进行分裂操作,直到这个过程传到根节点为止。
①应该将中间位置插入到节点所属指针右边的位置。

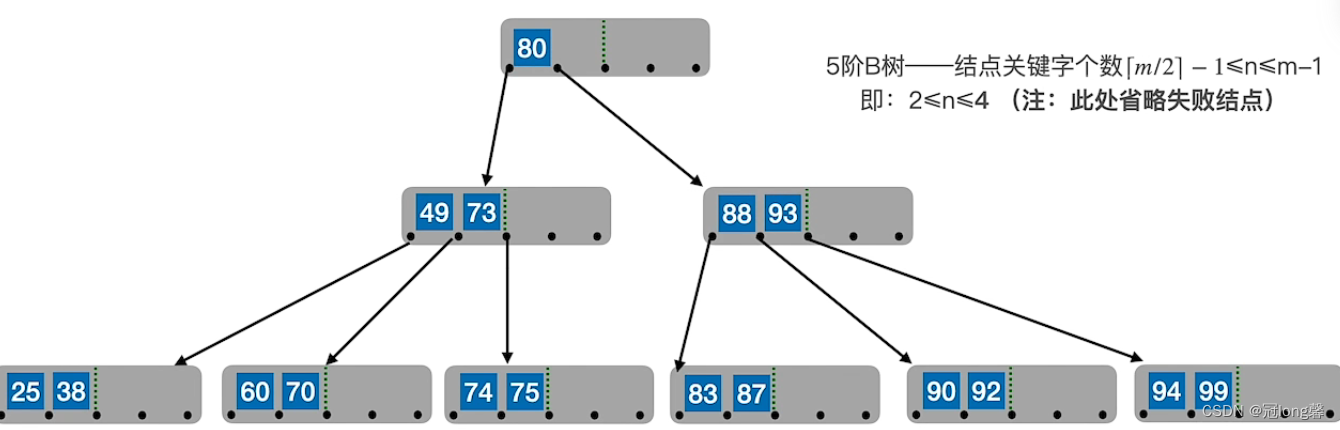
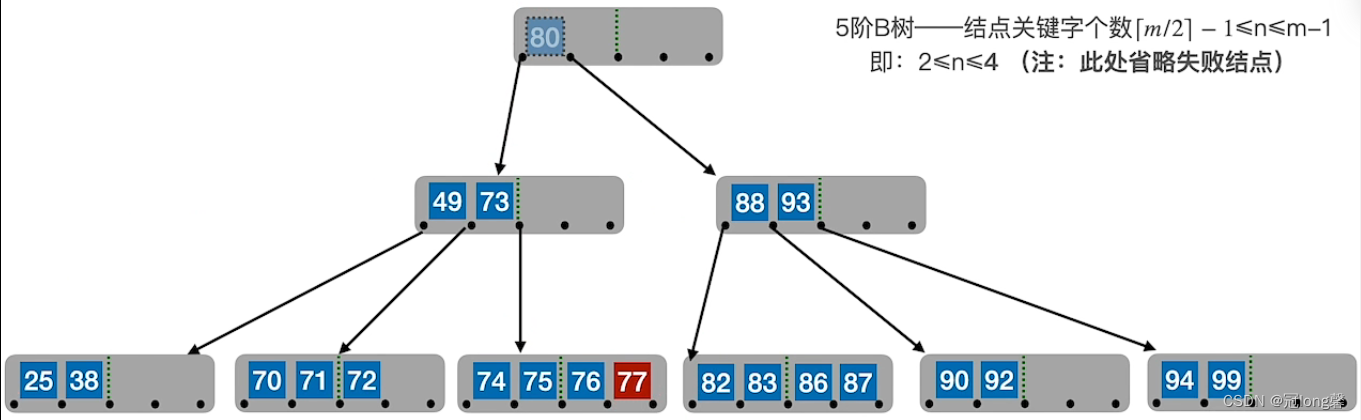
(3)B树的删除
-
非终端结点
:若删除关键字在非终端节点,则
用直接前驱或直接后继替代被删除的关键字,然后删除直接前驱或直接后继
。
①直接前驱:左侧指针子树中的最右下元素
②直接后继:右侧指针子树中的最左下元素
③对非终端结点的删除必然可以转化为对终端节点的删除操作。
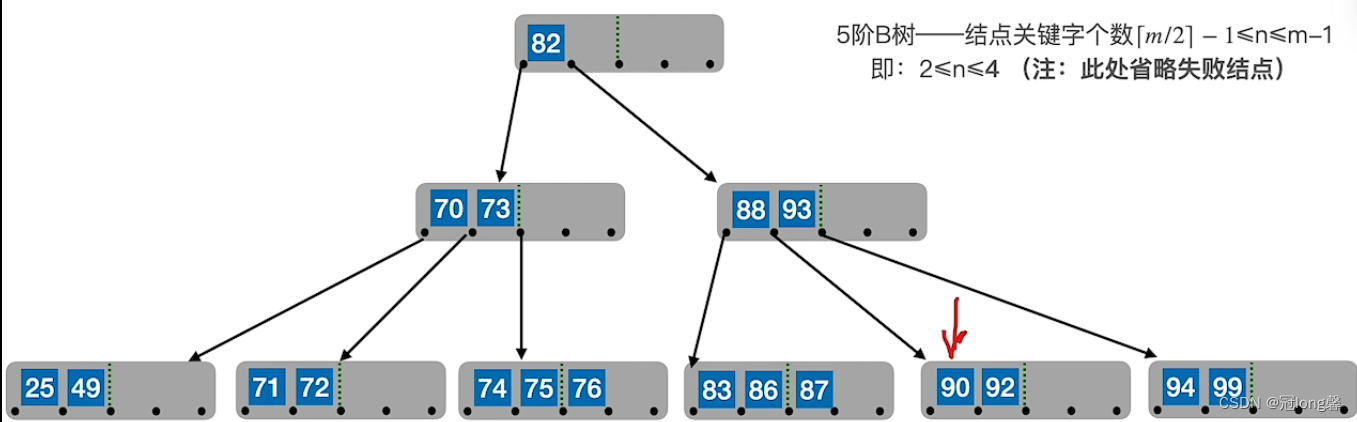
-
终端结点
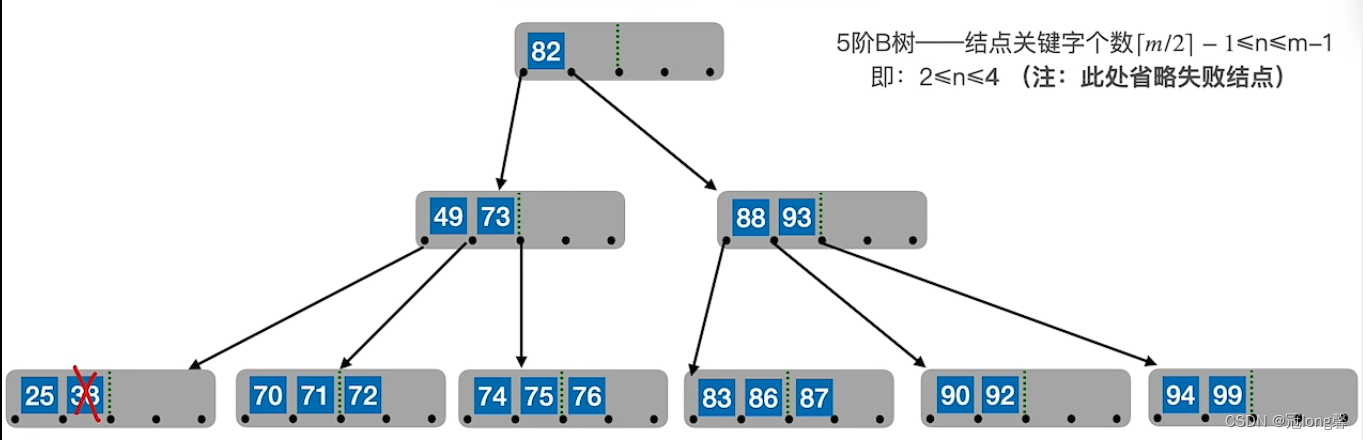
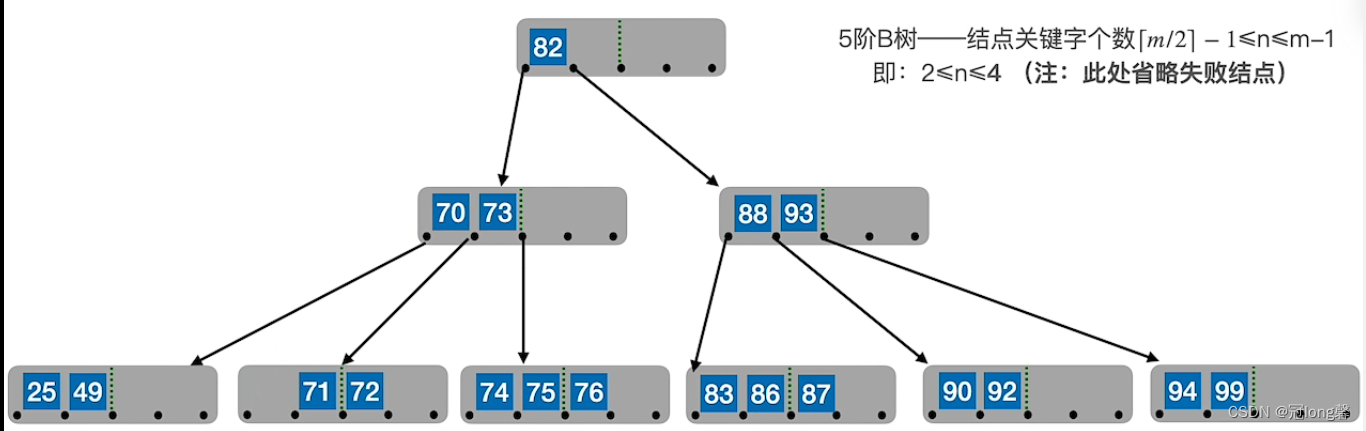
:若删除关键字在终端节点,则直接删除关键字。(要注意节点关键字个数是否低于下限[m/2]-1) -
关键字个数低于下限
:若被删除关键字所在结点删除后关键字个数低于下限,且与此结点右兄弟关键则个数还很宽裕,则需要调整该结点、右(左)兄弟结点及其双亲结点(
父子换位法
)。
①左兄弟宽裕时,用当前节点的前驱、前驱的前驱填补空缺。
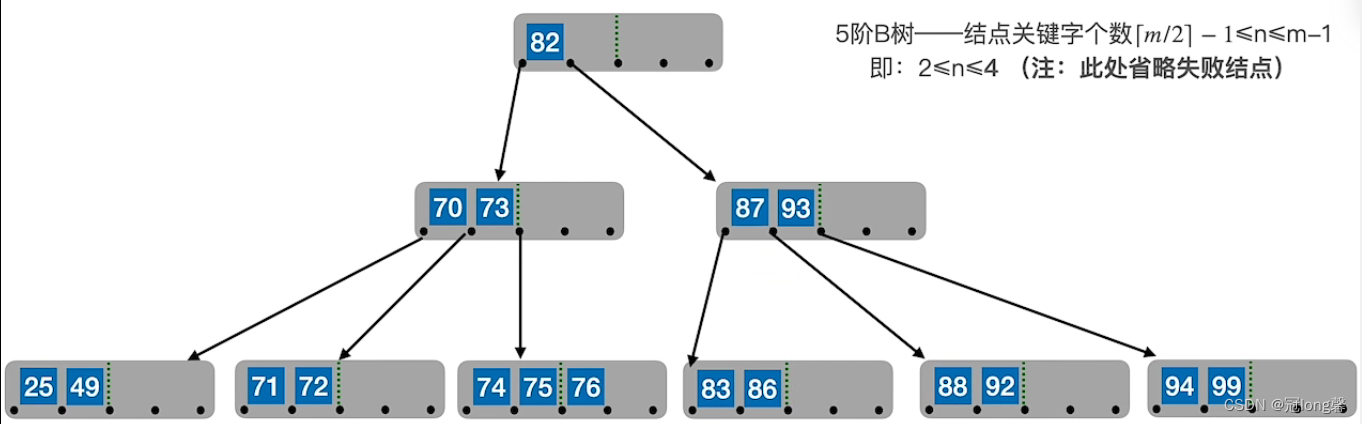
②右兄弟宽裕时,用当前节点的后继、后继的后继填补空缺。
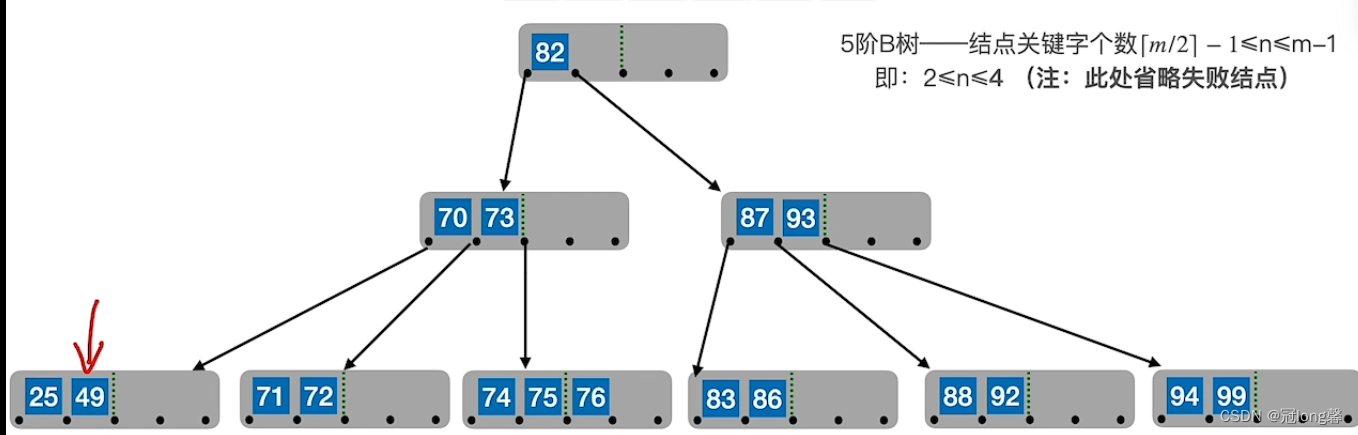
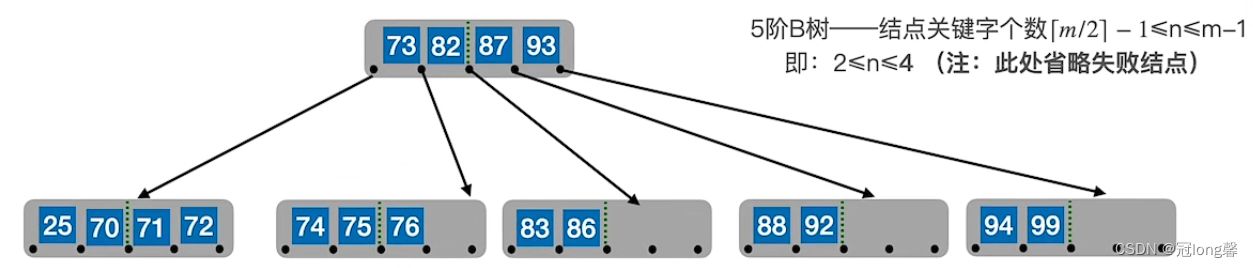
若兄弟不够借时,将兄弟节点及在双亲节点中间的关键字合并。若父节点的关键字个数低于下限时,则继续合并操作直到根节点
。
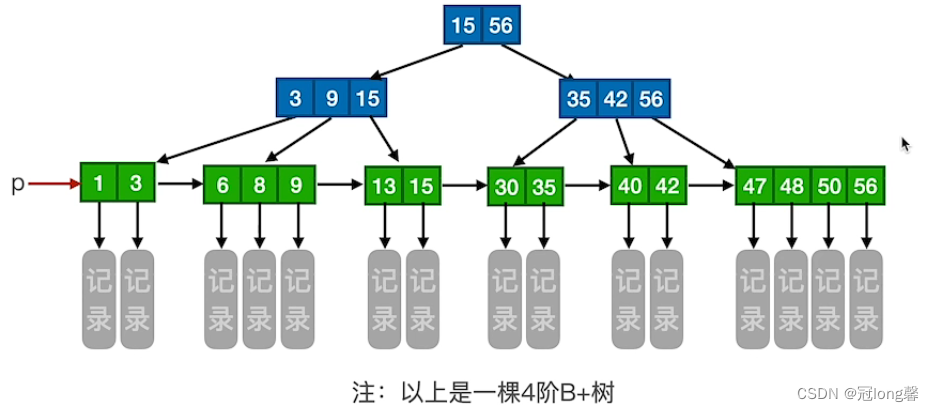
2. B+树的基本概念
(1)定义与性质
一棵m阶的B+树需满足下列条件:
- 每个分支结点最多有m棵子树。
-
非叶根节点至少有两颗子树(绝对平衡),其他每个分支结点至少有[m/2]棵子树。
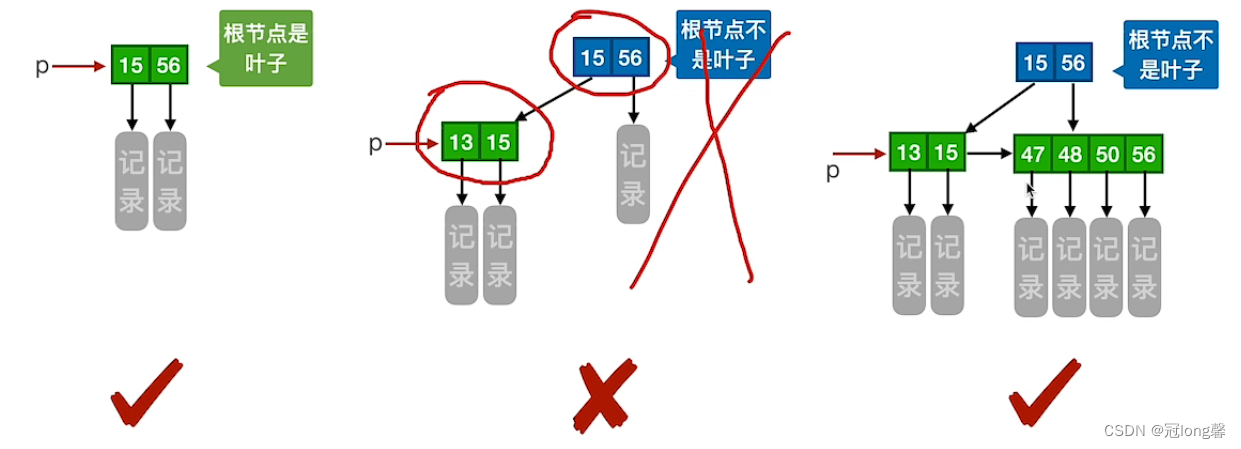
-
结点的子树个数与关键字个数相等
。 -
所有分支结点仅包含各个子节点中关键字的最大值,不包含对应关键字的存储信息
。 -
所有叶节点包含全部关键字及指向相应记录的指针
,叶节点中将关键字按大小顺序排列,并且
相邻叶节点按大小互相链接起来
。
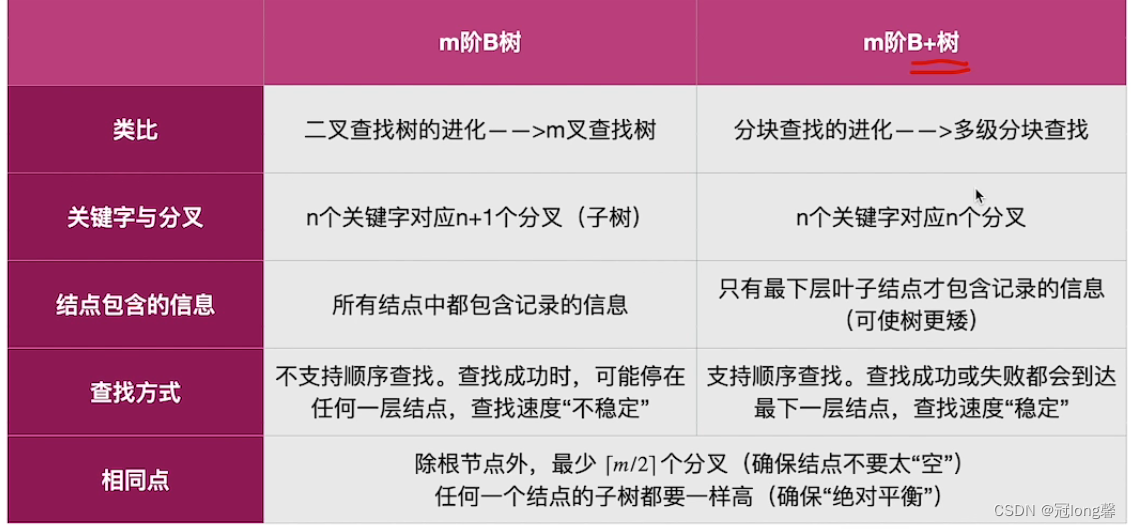
(2)B树与B+树的区别
-
B+树中n个关键字对应n棵子树,B+树中n个关键字对应n+1棵子树
. -
B+树中所有非叶节点仅起索引作用,而不包含关键字对应记录的存储地址
。B树中包含关键字及其存储信息。 -
非叶节点不含关键字对应记录的存储地址,使得磁盘块可以包含更多的关键字,使得
B+树的阶更大,树高更矮,读磁盘次数更少,查找更快
。