拟合性检验是用于分析实际次数与理论次数是否相同,适用于单个因素分类的计数数据。独立性检验用于分析各有多项分类的两个或两个以上的因素之间是否有关联或是否独立的问题。
2.卡方检验的应用条件
四格表:
1).随机样本数据;
2).卡方检验的理论频数不能太小。
两个独立样本比较可以分以下3种情况:
1.所有的理论数T≥5并且总样本量n≥40,用Pearson卡方进行检验。
2.如果理论数T<5但T≥1,并且n≥40,用连续性校正的卡方进行检验。
3.如果有理论数T<1或n<40,则用Fisher’s检验。
R×C表卡方检验应用条件:
1.R×C表中理论数小于5的格子不能超过1/5;
2.不能有小于1的理论数。我的实验中也不符合R×C表的卡方检验。可以通过增加样本数、列合并来实现。
3. Matlab实现
Matlab中有两个chi-square test相关函数:
4. Excel实现
Pearson χ2统计量
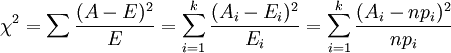
(i=1,2…)
利用Excel提供的CHIINV函数求临界值,如 =CHIINV(0.05, 5)
5. SPSS实现
类似Matlab,SPSS中也有两种方法:
分析——描述统计——交叉表
【注】a.使用第二种方法“交叉表”前,要先进行加权
b. 多于2行2列的R*C表,在交叉表——精确选项中应选Fisher精确检验
连续性校正卡方检验:仅适用于四格表资料,在n>40,所有期望频数均大于1,只有1/5单元格的期望频数大于1小于5时;
Fisher精确概率法:在样本含量<40或有格子的期望频数<1的列联表,应该采用该法;