博客

一 实验目的

实现一种用于车载网络的高精度实时入侵检测方法，该方法可以通过较少的工作量部署在当前的车载网关节点上。为达到此目的，所提出的入侵检测方法可以部署到车辆网关平台中的软件插件或者作为要加载到现有CAN总线上的硬件节点。设计实现一种基于固定数量的消息作为滑动窗口的信息熵监测算法，以及基于模拟退火算法对滑动窗口进行优化。

二 实验内容

1．给定固定大小的滑动窗口在CAN总线消息中实现基于信息熵检测的DoS攻击检测算法。

2．使用模拟退火算法改进实验一中算法的滑动窗口战略，优化决策条件，使得检测精度提高、假阳性率降低、响应时间缩短。

三 实验原理

1、CAN和DoS攻击

（1）CAN总线

CAN总线消息中，消息的优先级由其ID字段标识。正常情况下，在一定时间(或一定窗口)内取样得到的CAN总线消息，各ID段消息占据的比例应该不会出现大的波动，取样窗口的信息熵应处于一定的范围之内。

（2）DoS攻击

DoS攻击： 攻击者可以在总线上的短周期注入高优先级消息，影响CAN总线对于正常消息的处理，影响汽车电子系统的正常响应。

假设采样窗口的长度为w。由于DoS攻击的特性，在一个采样窗口内高优先级消息的比例会在短时间内增大，相应的低优先级的消息比例降低。这会导致采样窗口内信息熵的异常变化。

信息熵

：熵是信息学上代表随机变量的不确定度的度量。一个离散随机变量X的熵H(X)定义为

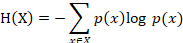
DoS攻击判断

：实验计算正常情况下CAN总线中信息熵的平均值a，标准差α,预测DoS攻击时设置决策条件区间（a-kα,a+kα），将信息熵超出决策条件的采样窗口预测为发生异常情况（即为DoS攻击）。其中k控制决策区间敏感度的常数。

2、性能评价指标

将一个采样（滑动）窗口看作一个块，那么定义：

1. 
   预测准确
   
   ：Ra=正确检测为攻击块的数目Da/攻击块总数Ta。
2. 
   假阳性率
   
   ：Rn=正常信息块被检测为攻击块的数目Dn/正常信息块的数目Tn。
3. 
   响应时间
   
   ：Rt=攻击开始时间At-攻击检测时间Dt。

3、模拟退火

模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。需要注意的是一定要徐徐冷却，也就是物体和外界温度相差越低，退火时间越长退火的效果就越好。这也就是这算法名字的由来。

该实验中的模拟退火步骤如下：

• 初始化 起始温度
  
t

  、下降率
  
t_dis

  、停止温度
  
t_min

  、温度下的寻找次数
  
step

• 生成初始解：窗口大小
  
w

  和 系数
  
k

  ，利用评价指标得到初始解分数
  
eva

• 生成新解，使用评价函数评价新解
  
eva_new

  • 如果新解Tn+1更优秀则接受新解。
  • 否则以一定概率p接受Tn+1
• 重复上一步骤，直到解足够优秀或温度降得足够低

四 实验条件

1、数据集：

• DoS_attack_dataset_no_zero.csv是未加入DoS攻击的正常CAN总线数据集；Add_DoS_attack_dataset1.csv是加了DoS攻击块的CAN总线数据集，DoS攻击块由ID=0标识。

2、建议使用python语言，可能需要的python包：pandas，math，matplotlib，numpy。

五 实验过程

1、计算正常信息熵

• 
  读取文件
  

• 
  滑动窗口
  

设置滑动窗口大小 w=100，比例系数 k = 2.5

• 
  计算信息熵
  

  • 
    信息熵
    

    以 w 的步长移动滑动窗口，得到各窗口内不同ID消息出现的频率，并计算窗口内的信息熵，信息熵公式如下，p（x）代表 ID=x 的信息块出现的频率

    

  • 
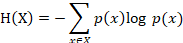
    均值和方差
    

    记录各窗口内的信息熵，最后得到无攻击下的信息熵
    
均值mean

    和
    
方差var


• 
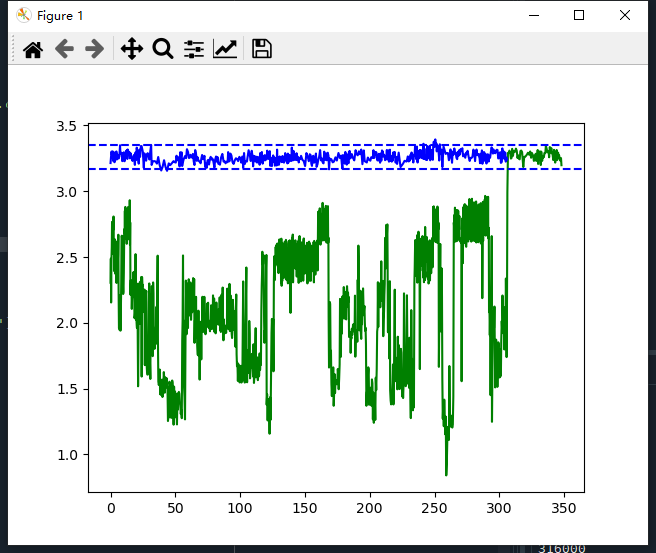
  绘图
  

绘制滑动窗口中的信息熵变化，并画出无攻击下的信息熵变化范围

• 
  代码
  

  • 无DOS攻击的信息熵
    
no_dos.py


    # DoS_attack_dataset_no_zero
    import pandas as pd
    import numpy as np
    import matplotlib.pyplot as plt
    
    # 1.读取csv文件
    df = pd.read_csv('data/DoS_attack_dataset_no_zero.csv', sep='\t')
    
    # 2.滑动窗口
    w=500
    k=2.5
    
    shang=[]  # 记录不同窗口的信息熵
    err_time=[]  # 记录时间戳
    for st in range(0,len(df),w):
        # 以w的步长移动窗口
        data = df.iloc[st:st+w]
        # 得到本窗口内第1条消息的时间戳的值
        end_time = data.iloc[0]['TimeStamp']
        err_time.append(end_time)
        # 得到窗口内不同ID消息出现的频率
        p_data = data['ID'].value_counts() / data['ID'].count()
        # 计算该窗口内的信息熵
        shang.append(-sum(p_data*np.log(p_data)))
        if st % 1000==0:
            print(st)
    
    # 计算无攻击下的信息熵均值和方差
    arr_mean = np.mean(shang)    
    arr_std = np.std(shang, ddof=1)
    print(arr_mean,arr_std)
    
    # 区间
    a=arr_mean-k*arr_std
    b=arr_mean+k*arr_std
    
    # 绘图
    plt.plot(err_time,shang,c='b')
    plt.axhline(y=a,ls='--',c='blue')
    plt.axhline(y=b,ls='--',c='blue')
    

  • 有DOS攻击的信息熵
    
dos.py


    # Add_DoS_attack_dataset1
    import pandas as pd
    import numpy as np
    import matplotlib.pyplot as plt
    
    # 读取csv文件
    df = pd.read_csv('data/Add_DoS_attack_dataset1.csv', sep='\t')
    w=500
    
    shang=[]
    err_time=[]
    k=2.5
    
    for st in range(0,len(df),w):
        # 以w的步长移动窗口
        data = df.iloc[st:st+w]
        # 得到本窗口内第1条消息的时间戳的值
        end_time = data.iloc[0]['TimeStamp']
        err_time.append(end_time)
        # 得到窗口内不同ID消息出现的频率
        p_data = data['ID'].value_counts() / data['ID'].count()
        # 计算该窗口内的信息熵
        shang.append(-sum(p_data*np.log(p_data)))
        if st % 1000==0:
            print(st)
    
    plt.plot(err_time,shang,c='g')
    

2、模拟退火

使用模拟退火算法更新参数

窗口大小w

和

比例系数 k


（1）读取数据

##1. 读取数据
df_no = pd.read_csv('data/DoS_attack_dataset_no_zero.csv', sep='\t')
df_dos = pd.read_csv('data/Add_DoS_attack_dataset1.csv', sep='\t')

（2）打表，标记各数据的攻击开始时间

初始化一个

dos_start

列表，用于记录每段连续攻击块的起始下标，若不属于攻击块，则下标置为-1

def attack_start(df_dos):
    pre_i = -1  # 下标初始化-1
    dos_start=[]
    df=df_dos.values
    flag=1  # flag=0代表出现（连续）攻击块
    for i in df[:,0]:
        if df[i,2]==0:  # 若是攻击块
            if flag==1:  # 且是新的连续攻击
                pre_i=i  # 起点置为当前下标
                flag=0   # 标记为连续攻击
        else:   # 若不是攻击块
            pre_i=-1  
            flag=1  # 标记为非攻击
        dos_start.append(pre_i)  # 记录下标
    return dos_start

##2. 打表，标记各数据的攻击开始时间
print("正在打表，标记攻击开始时间:")
dos_start=attack_start(df_dos)
print("打表完成")

（3）模拟退火

① 设定迭代次数和终止条件

初始温度为100，每次迭代温度下降，直至温度降到10

t = 100  # 初始温度
t_dis=0.98
t_min=10  # 停止温度

② 随机初始wk

随机初始化w和k

w=random.randrange(100,200)   # 窗口大小
k=random.uniform(1,3.5)   # 比例系数
x=[w,k]
print("初始解")
print("T = %.2f" % t,"w =",w,"k = %.2f"%k)

③计算信息熵和评估结果

用数据1计算无攻击下的信息熵的均值和方差。信息熵的正常范围取值为

（mean - k * var,mean + k * var）


用数据2评估是否存在攻击块。超出取值范围即视为攻击块。

评估指标：

• 预测准确：Ra=正确检测为攻击块的数目Da/攻击块总数Ta
• 假阳性率：Rn=正常信息块被检测为攻击块的数目Dn/正常信息块的数目Tn
• 响应时间：Rt=攻击开始时间At-攻击检测时间Dt

定义评估函数：

eva = 0.7*Ra-0.2*Rn-0.1*Rt

。可以自定义或查阅文献确定

def entropy(df_no,df_dos,x,dos_start,flag): 
    
    # 1.初始化
    num=0  # 攻击块数目
    ans=0  # 正确检测为攻击块个数
    err_ans=0 # 错误检测为攻击块个数
    t=[]  # 记录时间戳
    shang=[]  # 记录信息熵
    t_dos=[]
    shang_dos=[]
    df_no=df_no.values
    df_dos=df_dos.values
    
    # 2.用数据1计算信息熵均值和方差
    for st in range(0,len(df_no),x[0]):
        # 取出以st为起点，窗口大小为step的数据
        data = df_no[st:st+x[0]]
        # 得到本窗口内第1条消息的时间戳的值
        end_time = data[0,1]
        t.append(end_time)
        #得到窗口内不同ID消息出现的频率
        unique, counts = np.unique(data[:,2], return_counts=True)
        p_data = counts/np.sum(counts)
        # 计算熵
        shang.append(-sum(p_data*np.log(p_data)))

    # 计算均值和方差
    arr_std = np.std(shang, ddof=1)
    arr_mean = np.mean(shang)
    # 得到正常的信号区间
    a=arr_mean-x[1]*arr_std
    b=arr_mean+x[1]*arr_std
    
    # 3.用数据2检测受攻击块数
    res_time=[]  # 记录响应时间  
    for st in range(0,len(df_dos),x[0]):
        data = df_dos[st:st+x[0]]
        end_time = data[0,3]
        t_dos.append(end_time)
        unique, counts = np.unique(data[:,2], return_counts=True)
        p_data = counts/np.sum(counts)
        shang_t=-sum(p_data*np.log(p_data))  # 定义shang_t用于判断攻击块
        shang_dos.append(shang_t)
        
        # 若有ID=0,记录为攻击块
        if 0 in data[:,2]:
            num+=1
            # 是攻击块且正确检测
            if shang_t<a or shang_t>b:
                ans+=1
                # 计算响应时间
                dos_time=dos_start[st]  # 攻击更早开始，则有延时
                if dos_time==-1:
                    # temp=st
                    # while dos_start[temp]==-1:
                    #     temp+=1
                    dos_time=st    # 攻击在该窗口，当做无延迟
                res_time.append(df_dos[st,3]-df_dos[dos_time,3])
        else:
            # 不是攻击块被错误检测
            if shang_t<a or shang_t>b:
                err_ans+=1
            
    # 4.评估函数
    # 评估指标
    ra=ans/num  # 预测准确率
    rn=err_ans/(int(len(df_dos)/x[0])-num)  # 假阳性率
    rs=np.array(res_time)
    rs=np.mean((max(rs)-rs)/(max(rs)-min(rs)))  # 响应时间
    
    # 综合评估
    eva=0.4*ra+0.4*(1-rn)+0.2*rs
    print("预测准确率: %.2f"%ra,"假阳性率: %.2f"%rn,"响应时间: %.4f"%(1-rs),"评估指数: %.4f"%eva)
    if flag==1:
        plot_fig(t,shang,t_dos,shang_dos,a,b)
    return eva

④ 构造新解

def solution(x):
    x_new=[0,0]
    x_new[0] = int(x[0]+np.random.uniform(low=-10, high=10))
    while x_new[0]<0:
        x_new[0] = int(x[0]+np.random.uniform(low=-10, high=10))
    x_new[1] = x[1]+np.random.uniform(low=-0.3, high=0.3)
    while x_new[1]<0:
        x_new[1] = x[1]+np.random.uniform(low=-0.3, high=0.3)
    return x_new
    
x_new=solution(x)
# 新解的结果
eva_new=entropy(df_no,df_dos,x_new,dos_start,0)

⑤ 是否选择新解

在当前温度下寻找N次邻居生成N次新解，对于每次的新解：

• 若新解优于当前解，则将当前解更新

• 若新解不优于当前解，则以 p 的概率将当前解更新，p的公式如下：

  

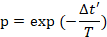
  • Δt = 新解的评估结果 – 旧解的评估结果

  • T 为当前温度

for i in range(step):
    # 构造新解w,k
    x_new=solution(x)
    print("T = %.2f" % t,"w =",x_new[0],"k = %.2f"%x_new[1])
    # 新解的结果
    eva_new=entropy(df_no,df_dos,x_new,dos_start,0)
    # 若新解更优秀，选择新解
    if eva_new>eva_cur:
        x=x_new
        eva_cur=eva_new
        print("新解更优,接受新解\n")
    else:
        # 否则，以 p 的概率接受新解
        p = math.exp(-(eva_cur - eva_new)*1000 / t)
        r = np.random.uniform(low=0,high=1)
        print("新解较差,以 %.2f 的概率接受新解"%p," → 随机 p = %.2f"% r)
        if r<p:
            x = x_new
            eva_cur = eva_new
            print("接受新解\n")
        else:
            print("拒绝新解\n")
    eva_ls.append(eva_cur)

⑥ 迭代

迭代上述过程，直至温度下降至阈值

3、加入模拟退火的完整代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import random
import math

# =============================================================================
# 计算信息熵均值和方差
# =============================================================================
def entropy(df_no,df_dos,x,dos_start,flag): 
    
    # 1.初始化
    num=0  # 攻击块数目
    ans=0  # 正确检测为攻击块个数
    err_ans=0 # 错误检测为攻击块个数
    t=[]  # 记录时间戳
    shang=[]  # 记录信息熵
    t_dos=[]
    shang_dos=[]
    df_no=df_no.values
    df_dos=df_dos.values
    
    # 2.用数据1计算信息熵均值和方差
    for st in range(0,len(df_no),x[0]):
        # 取出以st为起点，窗口大小为step的数据
        data = df_no[st:st+x[0]]
        # 得到本窗口内第1条消息的时间戳的值
        end_time = data[0,1]
        t.append(end_time)
        #得到窗口内不同ID消息出现的频率
        unique, counts = np.unique(data[:,2], return_counts=True)
        p_data = counts/np.sum(counts)
        # 计算熵
        shang.append(-sum(p_data*np.log(p_data)))

    # 计算均值和方差
    arr_std = np.std(shang, ddof=1)
    arr_mean = np.mean(shang)
    # 得到正常的信号区间
    a=arr_mean-x[1]*arr_std
    b=arr_mean+x[1]*arr_std
    
    # 3.用数据2检测受攻击块数
    res_time=[]  # 记录响应时间  
    for st in range(0,len(df_dos),x[0]):
        data = df_dos[st:st+x[0]]
        end_time = data[0,3]
        t_dos.append(end_time)
        unique, counts = np.unique(data[:,2], return_counts=True)
        p_data = counts/np.sum(counts)
        shang_t=-sum(p_data*np.log(p_data))  # 定义shang_t用于判断攻击块
        shang_dos.append(shang_t)
        
        # 若有ID=0,记录为攻击块
        if 0 in data[:,2]:
            num+=1
            # 是攻击块且正确检测
            if shang_t<a or shang_t>b:
                ans+=1
                # 计算响应时间
                dos_time=dos_start[st]  # 攻击更早开始，则有延时
                if dos_time==-1:
                    # temp=st
                    # while dos_start[temp]==-1:
                    #     temp+=1
                    dos_time=st    # 攻击在该窗口，当做无延迟
                res_time.append(df_dos[st,3]-df_dos[dos_time,3])
        else:
            # 不是攻击块被错误检测
            if shang_t<a or shang_t>b:
                err_ans+=1
            
    # 4.评估函数
    # 评估指标
    ra=ans/num  # 预测准确率
    rn=err_ans/(int(len(df_dos)/x[0])-num)  # 假阳性率
    rs=np.array(res_time)
    rs=np.mean((max(rs)-rs)/(max(rs)-min(rs)))  # 响应时间
    
    # 综合评估
    eva=0.5*ra+0.3*(1-rn)+0.2*rs
    print("预测准确率: %.2f"%ra,"假阳性率: %.2f"%rn,"响应时间: %.4f"%(1-rs),"评估指数: %.4f"%eva)
    if flag==1:
        plot_fig(t,shang,t_dos,shang_dos,a,b)
    return eva

# =============================================================================
# 构造新解
# =============================================================================
def solution(x):
    x_new=[0,0]
    x_new[0] = int(x[0]+np.random.uniform(low=-10, high=10))
    while x_new[0]<=30:
        x_new[0] = int(x[0]+np.random.uniform(low=-10, high=10))
    x_new[1] = x[1]+np.random.uniform(low=-0.3, high=0.3)
    while x_new[1]<=1:
        x_new[1] = x[1]+np.random.uniform(low=-0.3, high=0.3)
    return x_new

# =============================================================================
# 绘图
# =============================================================================
def plot_fig(t,shang,t_dos,shang_dos,a,b):
    plt.plot(t,shang,c='b',label='No_DOS_Attack')
    plt.plot(t_dos,shang_dos,c='g',label='Exist_DOS_Attack')
    plt.legend()
    plt.axhline(y=a,ls='--',c='y')
    plt.axhline(y=b,ls='--',c='y')
    
    # ax=fig.add_subplot(121)
    # ax.plot(t,shang,c='b',label='No_DOS_Attack')
    # ax.plot(t_dos,shang_dos,c='g',label='Exist_DOS_Attack')
    # ax.xlabel('TimeStamp')
    # ax.ylabel('Entropy')
    # plt.axhline(y=a,ls='--',c='y')
    # plt.axhline(y=b,ls='--',c='y')
    # plt.legend()
    # plt.show()

# =============================================================================
# 打表，标记各数据的攻击开始时间
# =============================================================================
def attack_start(df_dos):
    pre_i = -1  # 下标初始化-1
    dos_start=[]
    df=df_dos.values
    flag=1  # flag=0代表出现（连续）攻击块
    for i in df[:,0]:
        if df[i,2]==0:  # 若是攻击块
            if flag==1:  # 且是新的连续攻击
                pre_i=i  # 起点置为当前下标
                flag=0   # 标记为连续攻击
        else:   # 若不是攻击块
            pre_i=-1  
            flag=1  # 标记为非攻击
        dos_start.append(pre_i)  # 记录下标
    return dos_start
    
    
if __name__ == '__main__':
    
    ##1. 读取数据
    df_no = pd.read_csv('data/DoS_attack_dataset_no_zero.csv', sep='\t')
    df_dos = pd.read_csv('data/Add_DoS_attack_dataset1.csv', sep='\t')
    
    ##2. 打表，标记各数据的攻击开始时间
    print("正在打表，标记攻击开始时间:")
    dos_start=attack_start(df_dos)
    print("打表完成")
    
    ##3. 模拟退火优化w和k
    #3.1 设定迭代次数和终止条件
    t = 100  # 初始温度
    t_dis=0.98
    step=10  # 每个温度下迭代次数
    t_min=1  # 停止温度
    
    #3.2 随机初始解
    # w=random.randrange(100,200)   # 窗口大小
    # k=random.uniform(2,3)   # 比例系数
    w=100
    k=5
    x=[w,k]
    print("初始解")
    print("T = %.2f" % t,"w =",w,"k = %.2f"%k)
    
    # 初始解的结果
    eva_cur=entropy(df_no,df_dos,x,dos_start,0)
    eva_ls=[eva_cur]
    temp=8000
    
    #3.3 模拟退火
    print("\n模拟退火迭代:")
    while t>=t_min:
        for i in range(step):
            # 构造新解w,k
            x_new=solution(x)
            print("T = %.2f" % t,"w =",x_new[0],"k = %.2f"%x_new[1])
            # 新解的结果
            eva_new=entropy(df_no,df_dos,x_new,dos_start,0)
            # 若新解更优秀，选择新解
            if eva_new>eva_cur:
                x=x_new
                eva_cur=eva_new
                print("新解更优,接受新解\n")
            else:
                # 否则，以 p 的概率接受新解
                p = math.exp(-(eva_cur - eva_new)*temp / t)
                r = np.random.uniform(low=0,high=1)
                print("新解较差,以 %.2f 的概率接受新解"%p," → 随机 p = %.2f"% r)
                if r<p:
                    x = x_new
                    eva_cur = eva_new
                    print("接受新解\n")
                else:
                    print("拒绝新解\n")
        eva_ls.append(eva_cur)
        t = t_dis*t
        # print("T = %.2f" % t,"w =",w,"k = %.2f"%k)
        
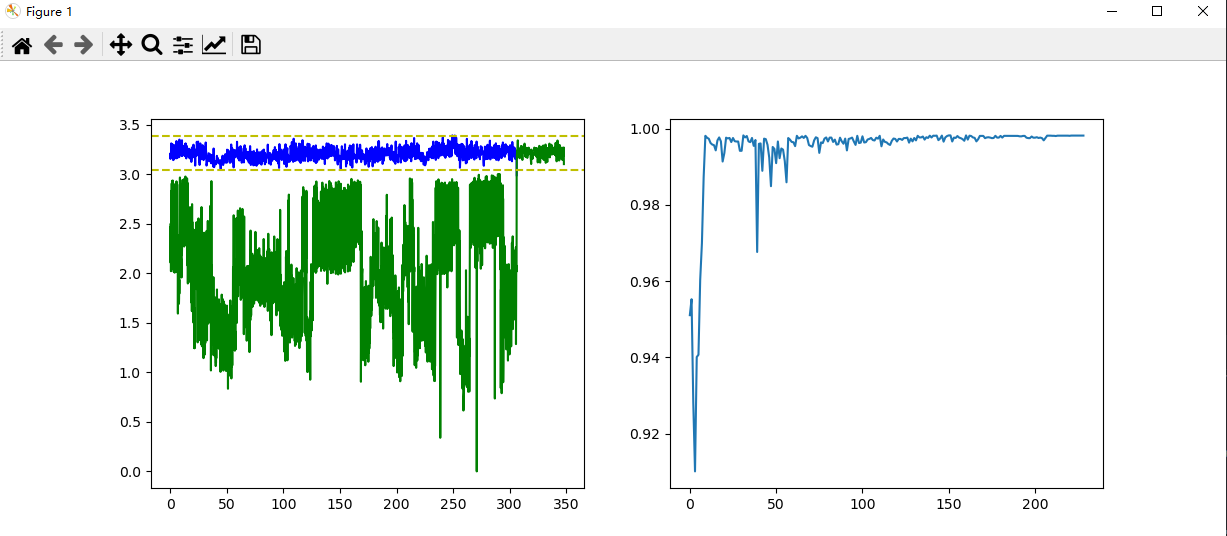
    ## 4. 输出结果并绘制图像
    # 4.1 绘制信息熵和判断范围图
    fig = plt.figure()
    ax = fig.add_subplot(121)
    entropy(df_no,df_dos,x,dos_start,flag=1)
    
    # 4.2 绘制评估指标变化图
    ax = fig.add_subplot(122)
    plt.plot(eva_ls)