1 递归(Recursion)
1.1 特点
(1)递归 – 循环,通过函数体来进行的循环;
(2)盗梦空间的梦境

1.2 递归状态
(1)示例

1.3 注意要点
(1)警惕堆栈溢出:如果递归求解的数据规模很大,调用层次很深,一直压入栈就会有堆栈溢出的风险;在代码中限制最大递归深度超过深度就抛错;
(2)警惕重复计算:通过比如散列表保存已求解的结果,空间复杂度从O(n) 变成O(1);
(3)警惕生产环境脏数据导致死循环:如果A的推荐人是B,B的推荐人是C,C的推荐人是A,解决方式是判断环;
1.4 递归思维要点
(1)不要人肉进行递归(最大误区),初学者可以在纸上画出递归的状态树,慢慢熟练之后一定要抛弃这样的习惯。一定要记住:直接看函数本身开始写即可。否则,永远没办法掌握、熟练使用递归;
(2)找到最近最简的方法,将其拆解成可重复解决的问题(找最近重复子问题)。原因是我们写的程序的指令,只包括 if else 、 for 和 while loop、递归调用;
(3)数学归纳法的思维,最开始最简单的条件是成立的,比如n=1,n=2的时候是成立的,且第二点你能证明当n成立的时候,可以推导出n+1也成立的;
1.5 递归代码模板
public void recur(int level, int param) {
// 1.递归终结条件(最先写)
if (level > MAX_LEVEL) {
// process result
return;
}
// 2.处理当前层逻辑
process(level, param);
// 3.下探到下一层
recur( level: level + 1, newParam);
// 4.清理恢复当前层
revertStates();
}
1.4 小结
碰到一个题目,就会找到他的重复性:
(1)最优重复性:动态规划;
(2)最近重复性:根据重复性的构造和分解,便有分治和回溯。
2 分治(Divide & Conquer)
2.1 特点
(1)分治和回溯,本质上就是递归,是递归的一个细分类。可以理解为分治和回溯,就是一种特殊的递归,或者是较为复杂的递归;
(2)大问题由细的子问题组成;
(3)分治的思想:本质是递归,在递归状态树的时候;找最近重复性,将大问题分为子问题分别解决,再组合子问题的结果为最终结果。具体分析:字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
2.2 递归状态树
(1)示例
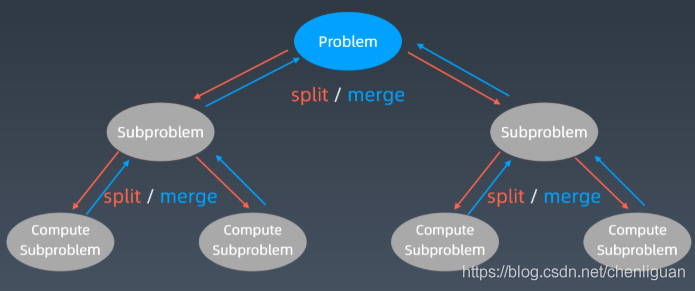
2.3 分治法的基本步骤
(1)分治算法能解决的问题,一般需要满足下面这几个条件:
(2)原问题与分解成的小问题具有相同的模式
(3)原问题分解成的子问题可以独立求解,子问题之间没有相关性
(4)具有分解终止条件,也就是说,当问题足够小,可以直接求解
(5)可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了
2.4 分治代码模板
public void recur(int level, int param) {
// 1.递归终结条件(最先写)
if (level > MAX_LEVEL) {
// process result
return;
}
// 2.处理当前层逻辑
process(level, param);
// 3.调用函数下探到下一层,解决更细节的子问题
int subresult1 = recur( level: level + 1, newParam);
int subresult2 = recur( level: level + 1, newParam);
int subresult3 = recur( level: level + 1, newParam);
// 4.将子问题的解的合并,产生最终结果
int result = processResult(subresult1, subresult2, subresult3, …);
// 5.清理恢复当前层
revertStates();
}
3 回溯(Backtracking)

3.1 特点
(1)回溯法采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算;再回到上一层,去试其他的可能答案。
(2)回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:①找到一个可能存在的正确的答案;②在尝试了所有可能的分步方法后宣告该问题没有答案。在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。
(3)最典型的应用是:八皇后问题、数独。
3.2 一般步骤
(1)针对所给问题,确定问题的解空间:首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解;
(2)确定结点的扩展搜索规则;
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
5 贪心算法(Greedy)
贪心算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。
贪心算法可以认为是动态规划算法的一个特例,相比动态规划,使用贪心算法需要满足更多的条件(贪心选择性质),但是效率比动态规划要高。
比如说一个算法问题使用暴力解法需要指数级时间,如果能使用动态规划消除重叠子问题,就可以降到多项式级别的时间,如果满足贪心选择性质,那么可以进一步降低时间复杂度,达到线性级别的。
5.1 特点
(1)特质:每一步都做出一个局部最优的选择,最终的结果就是全局最优。注意哦,这是一种特殊性质,其实只有一部分问题拥有这个性质。
比如你面前放着 100 张人民币,你只能拿十张,怎么才能拿最多的面额?显然每次选择剩下钞票中面值最大的一张,最后你的选择一定是最优的。
然而,大部分问题明显不具有贪心选择性质。比如打斗地主,对手出对儿三,按照贪心策略,你应该出尽可能小的牌刚好压制住对方,但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法,而得使用动态规划解决,参见前文「动态规划解决博弈问题」。
(2)每一步都需要选择,且不能回退。
(3)此方法可能鼠目寸光,未必当前选了最好的选择,全局就是最优,所以贪心算法需要满足一些前置条件方可使用合适。
(4)做题的时候贪心的思路要考虑的巧妙一点,比如从前往后贪心,或从后往前贪心。

5.2 场景
(1)贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。

(2)贪心法可以做为辅助算法,解决对结果不特别精确的问题

5.3 贪心、回溯、和动态规划的对比
(1)贪心:当下做局部最优判断;
(2)回溯:能够回退;
(3)动态规划:最优判断+回退;
5.4 例子
(1)当硬币可选集合固定:Coins = [20, 10, 5, 1],求最少可以几个硬币拼出总数。 比如 total = 36。前提条件:比如 Coin Change 这个题目,每个硬币都是倍数关系。
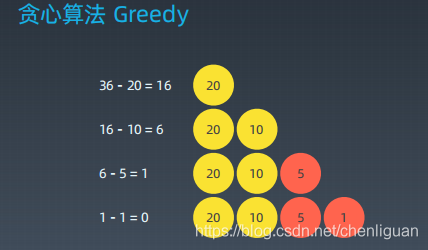
(2)反例

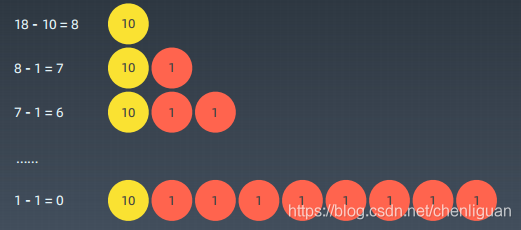
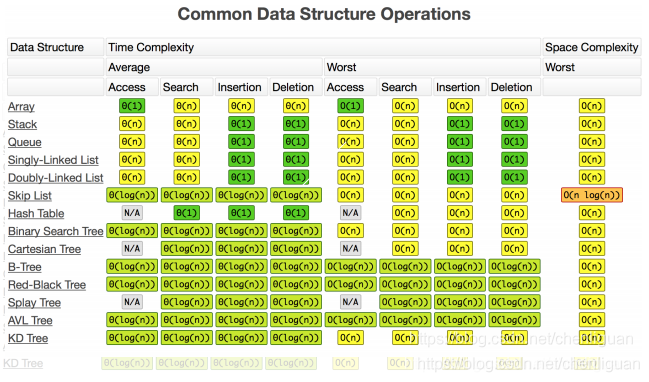
6 时间空间复杂度汇总