博客

随机过程（二）泊松过程

  • Post author:
  • Post category:其他


文章目录

泊松过程是一类较为简单的时间连续状态离散的随机过程。



1. 定义


计数过程


在这里插入图片描述


不同时间段内增量相互独立——独立增量过程


在这里插入图片描述


不同时间段内增量仅与时间差有关——平稳增量过程


在这里插入图片描述


泊松过程


在这里插入图片描述

由定义可知，泊松过程既是独立增量过程，也是平稳增量过程。

根据这个定义来判断是否是泊松过程，则需要判断是否满足三个条件。条件1容易判断；条件2通常可以通过对过程了解的情况去验证；条件3是较为难检验的。因此给出下面另一个定义。

在这里插入图片描述

简单理解即是，在充分小的时间内，最多有一个事件发生。



2. 基本性质



2.1 数字特征


均值函数


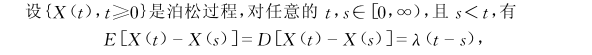
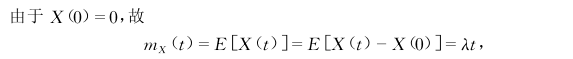
在这里插入图片描述

在这里插入图片描述


方差函数


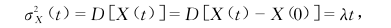
在这里插入图片描述


自相关函数


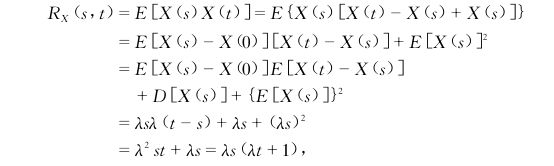
在这里插入图片描述


协方差函数


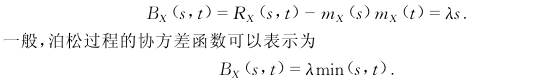
在这里插入图片描述


特征函数


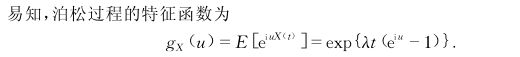
在这里插入图片描述



2.2 时间间隔与等待时间的分布

在这里插入图片描述


泊松过程时间间隔序列的分布是指数分布


在这里插入图片描述

该定理的结论是在平稳独立增量过程的假设前提下得到的，改假设的概率意义是指

过程在任意时刻都得从头开始

，即从任何时刻起过程独立于先前已经发生的一切（独立）；且

有与原过程完全一样的分布

（平稳）。


泊松过程等待时间的分布是



Γ

\Gamma






Γ





分布，该分布也叫爱尔兰分布


在这里插入图片描述



2.3 到达时间的条件分布

在这里插入图片描述


证明


在这里插入图片描述

在这里插入图片描述



3. 非齐次泊松过程

对泊松过程进行推广，允许时刻t的来到强度（速率）是t的函数。

在这里插入图片描述


非齐次泊松过程的概率分布


在这里插入图片描述



4. 复合泊松过程


定义


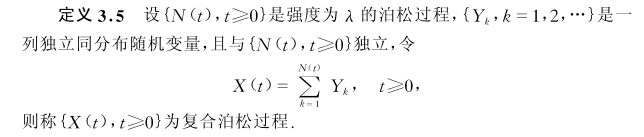
在这里插入图片描述


例子


在这里插入图片描述


复合泊松过程的性质


在这里插入图片描述


版权声明：本文为weixin_44523972原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。