博客

C/C++数据结构之深入理解红黑树原理和实现过程

  • Post author:
  • Post category:其他

红黑树

一、含义

红黑树是一个二叉排序树，是key-value结构。红黑树是强查找的数据结构。
强查找特性的数据结构有：
（1）红黑树。
（2）跳表。
（3）hash。
（4）B/B+数

1

2

3

4

5

6

7

8

9

header

红黑树具有一下性质：
（1）每个结点不是红的就是黑的；
（2）根结点是黑的；
（3）每个叶子结点是黑的；
（4）如果一个结点是红的，则它的两个儿子是黑的；
（5）对每个节点，从该结点到其子孙结点的所有路径上，都包含相同数目的黑结点；即黑高。这决定红黑树的平衡。
（6）一个结点到叶子节点最长的黑结点路径和最短黑结点路径 关系为 (2*n-1):1。

二、应用场景

（1）hashmap。
（2）CFS。完全公平算法
（3）epoll。
（4）定时器。
（5）nginx

三、代码实现红黑树

3.1、定义红黑树

/**********************定义红黑树 start***************************/
typedef int KEY_TYPE;

// 红黑树模板，提高复用性
#define RBTREE_ENTRT(name,type)	\
	struct name{				\
		struct type *right;		\
		struct type *left;		\
		struct type *parent;	\
		unsigned char color;	\
	}

typedef struct _rbtree_node {
	KEY_TYPE key;
	void *value;
#if 0
	struct _rbtree_node *right;
	struct _rbtree_node *left;
	struct _rbtree_node *parent;

	unsigned char color;
#else
	RBTREE_ENTRT(, _rbtree_node) node;
	//RBTREE_ENTRT(, _rbtree_node) node2;
#endif
}rbtree_node;

typedef struct _rbtree {
	rbtree_node *root;
	rbtree_node *nil;
}rbtree;

/**********************定义红黑树 end***************************/

3.2、红黑树的旋转

当红黑树的性质被破环时，需要触发旋转，进行调整。
旋转有两种方式：左旋和右旋。
红黑树插入或删除节点，最多需要旋转的次数是树的高度。
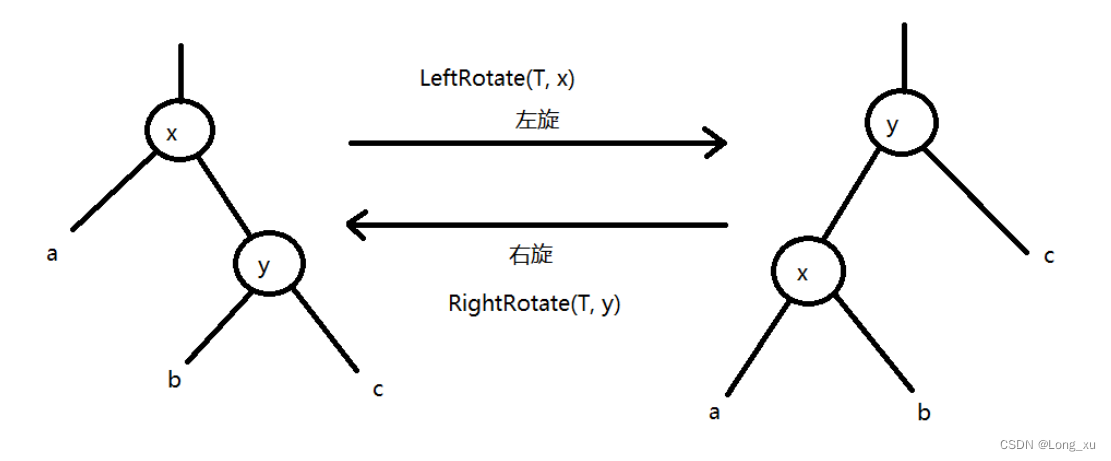
Rotate
以根结点示例：

左旋

右旋

6

root

4

2

1

3

5

8

7

9

1

2

3

4

5

6

7

8

9

root

左旋需要改变三个方向共六个指针的指向：X的右指针、Y的左指针，X父结点的指针；这三个指针是双向的，所以是六个指针（比如X的右指针指向Y，Y的父指针指向X）。即X的右指针改为指向Y的左结点，Y的左指针改为指向X，X的父结点指针改为指向Y。
右旋与左旋同理。

/**********************红黑树左旋 start***************************/
void rbtree_left_rotate(rbtree *T,rbtree_node *x)
{
	rbtree_node *y = x->node.right;
	// 1
	x->node.right = y->node.left;
	if (y->node.left != T->nil)
	{
		y->node.left->node.parent = x;
	}
	// 2
	y->node.parent = x->node.parent;
	if (x->node.parent == T->nil)
		T->root = y;
	else if (x == x->node.parent->node.left)
		x->node.parent->node.left = y;
	else
		x->node.parent->node.right = y;
	// 3
	y->node.left = x;
	x->node.parent = y;
}
/**********************红黑树左旋 end***************************/

/**********************红黑树右旋 start***************************/
/*
* x改为y，y改为x，右改为左，左改为右
*/
void rbtree_right_rotate(rbtree *T, rbtree_node *y)
{
	rbtree_node *x = y->node.left;
	// 1
	y->node.left = x->node.right;
	if (x->node.right != T->nil)
	{
		x->node.right->node.parent = y;
	}
	// 2
	x->node.parent = y->node.parent;
	if (y->node.parent == T->nil)
		T->root = x;
	else if (y == y->node.parent->node.right)
		y->node.parent->node.right = x;
	else
		y->node.parent->node.left = x;
	// 3
	x->node.right = y;
	y->node.parent = x;
}
/**********************红黑树右旋 end***************************/

3.3、红黑树插入结点

红黑树插入结点之前，它已经是一颗红黑树。插入的结点上的色是红色，因为这样不会改变黑高； 然后做调整。

红黑树插入结点时要插到底部。至于插入的key是否已存在，取决于业务场景，不属于红黑树的管理。

当插入结点时，可以推断出以下情况（比如插入的结点是z）：
（1）z是红色；
（2）z的父节点；
（3）z的祖父结点是黑色；
（4）z的叔结点不确定。

因此，插入情况：

右旋

父结点是左子树并且叔结点是黑色, z = 8

8

10

14

20

nil

调整后

8

10

14

nil

20

父结点是左子树并且叔结点是红色, z = 10

8

10

14

20

nil

调整后

8

14

20

10

nil

3.3.1、父结点是祖父结点的左子树的情况

（1）叔结点是红色的。

调整前 z=89,y=789

123

89

345

789

nil

调整后 z=345

123

345

789

89

nil

调整前 z=89,y=789

123

234

345

789

nil

调整后 z=345

123

345

789

89

nil 

if (z->node.parent == z->node.parent->node.parent->node.left)
{
	rbtree_node *y = z->node.parent->node.parent->node.right;
	if (y->node.color == RED)//叔父结点为红色
	{
		z->node.parent->node.color = BLACK;
		y->node.color = BLACK;
		z->node.parent->node.parent->node.color = RED;

		// 保证 Z 永远是红色，才能调整
		z = z->node.parent->node.parent;
	}
	else  //y==black
	{
		// ...
	}
}
else
{
	// ...
}

（2）叔结点是黑色的，而且当前结点是左孩子。
判断数是否一边重一边轻? 两个红节点相邻，并且z是父节点的左子树。以其祖父结点做右旋。
旋转前，将父结点改为黑色，祖父结点改为红色。

调整前 z=123,y=789

89

123

140

145

150

189

345

789

921

nil

nil

调整后 z=123

123

150

345

89

145

140

nil

189

789

nil

921 

rbtree_node *y = z->node.parent->node.parent->node.right;
if (y->node.color == RED)//叔结点为红色
{
	// ...
}
else  //y==black
{
	if(z==z->node.parent->node.left){
		z->node.parent->node.color = BLACK;
		z->node.parent->node.parent->node.color = RED;
		//祖父结点旋转
		rbtree_right_rotate(T, z->node.parent->node.parent);
	}
	// ...
}

（3）. 叔结点是黑色的，而且当前结点是右孩子
这种情况无法一步到位，需要经过中间桥梁–上述的【2】。即需要先转换为【2】中的开始，再由【2】转到最终平衡。
左旋之前需要将z=父节点。

调整后 z=123

89

123

140

145

150

189

345

789

nil

921

nil

调整前 z=150, y=789

345

123

89

150

145

189

140

nil

789

nil

921 

if (z == z->node.parent->node.right)
{
	z = z->node.parent;
	rbtree_left_rotate(T, z);
}
z->node.parent->node.color = BLACK;
z->node.parent->node.parent->node.color = RED;
//祖父结点旋转
rbtree_right_rotate(T, z->node.parent->node.parent);

3.3.2、父结点是祖父结点的右子树的情况

这种情况和【父结点是祖父结点的左子树的情况】同理。
具体代码实现如下：

rbtree_node *y = z->node.parent->node.parent->node.left;
if (y->node.color == RED)//叔父结点为红色
{
	z->node.parent->node.color = BLACK;
	y->node.color = BLACK;
	z->node.parent->node.parent->node.color = RED;

	// 保证 Z 永远是红色，才能调整
	z = z->node.parent->node.parent;
}
else {
	if (z == z->parent->left) {
		z = z->parent;
		rbtree_right_rotate(T, z);
	}

	z->parent->color = BLACK;
	z->parent->parent->color = RED;
	rbtree_left_rotate(T, z->parent->parent);
}

3.3.3、示例代码

/**********************红黑树插入 start***************************/
// 调整
void rbtree_insert_fixup(rbtree *T, rbtree_node *z)
{
	// 红黑树特性之一：如果一个结点是红的，则它的两个儿子是黑的
	while (z->node.parent->node.color == RED)
	{
		if (z->node.parent == z->node.parent->node.parent->node.left)
		{
			rbtree_node *y = z->node.parent->node.parent->node.right;
			if (y->node.color == RED)//叔父结点为红色
			{
				z->node.parent->node.color = BLACK;
				y->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;

				// 保证 Z 永远是红色，才能调整
				z = z->node.parent->node.parent;
			}
			else  //y==black
			{
				if (z == z->node.parent->node.right)
				{
					z = z->node.parent;
					rbtree_left_rotate(T, z);
				}
				z->node.parent->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;
				//祖父结点旋转
				rbtree_right_rotate(T, z->node.parent->node.parent);
			}
		}
		else
		{
			rbtree_node *y = z->node.parent->node.parent->node.left;
			if (y->node.color == RED)//叔父结点为红色
			{
				z->node.parent->node.color = BLACK;
				y->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;

				// 保证 Z 永远是红色，才能调整
				z = z->node.parent->node.parent;
			}
			else {
				if (z == z->node.parent->node.left) {
					z = z->node.parent;
					rbtree_right_rotate(T, z);
				}

				z->node.parent->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;
				rbtree_left_rotate(T, z->node.parent->node.parent);
			}
		}
	}
	T->root->node.color = BLACK;
}
// 插入到底部
void rbtree_insert(rbtree *T, rbtree_node *z)
{
	rbtree_node *y = T->nil;
	rbtree_node *x = T->root;
	while (x != T->nil)
	{
		y = x;
		if (z->key < x->key)
			x = x->node.left;
		else if (z->key > x->key)
			x = x->node.right;
		else
			return;
	}

	z->node.parent = y;
	if (y == T->nil)
		T->root = z;
	else {
		if (y->key > z->key)
			y->node.left = z;
		else
			y->node.right = z;
	}

	
	z->node.left = z->node.right = T->nil;
	z->node.color = RED;
	rbtree_insert_fixup(T, z);


}

/**********************红黑树插入 end***************************/

3.4、红黑树删除结点

红黑树删除的结点有几个情况：
（1）结点没有左右子树。

删除后

10

15

8

nil

16

nil

20

删除 z=13

8

10

20

13

15

16

nil

（2）结点有左子树或右子树。

删除后

10

15

8

13

20

删除 z=16

8

10

20

13

15

16

nil

代码实现：

	rbtree_node *x = T->nil;
	rbtree_node *y = T->nil;

	if ((z->node.left == T->nil) || z->node.right == T->nil)
		y = z;
	else
	{
		// ...
	}

	if (y->node.left != T->nil)
		x = y->node.left;
	else if (y->node.right != T->nil)
		x = y->node.right;

	x->node.parent = y->node.parent;
	if (y->node.parent == T->nil)
		T->root = x;
	else if (y == y->node.parent->node.left)
		y->node.parent->node.left = x;
	else
		y->node.parent->node.right = x;

（3）结点有左子树且有右子树

删除后

11

15

8

13

12

14

16

nil

20

中间状态

替换

10

15

8

13

12

14

16

nil

20

11

删除 z=10

8

10

11

20

13

14

15

16

nil

nil

12

代码实现：

rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
	while (x->node.left != T->nil) {
		x = x->node.left;
	}
	return x;
}

rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
	while (x->node.right != T->nil) {
		x = x->node.right;
	}
	return x;
}

rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x)
{
	if (x->node.right != T->nil)
	{
		return rbtree_mini(T, x->node.right);
	}

	rbtree_node *y = x->node.parent;
	while ((y != T->nil) && (x == y->node.right)) {
		x = y;
		y = y->node.parent;
	}
	return y;
}

rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) 
{
	rbtree_node *x = T->nil;
	rbtree_node *y = T->nil;

	if ((z->node.left == T->nil) || z->node.right == T->nil)
		y = z;
	else
	{
		y=rbtree_successor(T, z);
	}

	if (y->node.left != T->nil)
		x = y->node.left;
	else if (y->node.right != T->nil)
		x = y->node.right;

	x->node.parent = y->node.parent;
	if (y->node.parent == T->nil)
		T->root = x;
	else if (y == y->node.parent->node.left)
		y->node.parent->node.left = x;
	else
		y->node.parent->node.right = x;

	if (y != z)
	{
		z->key = y->key;
		z->value = y->value;
	}
	
	// 调整
	// ...

	return y;
}

3.4.1、当前结点是父结点的左子树的情况

（1）当前结点的兄弟结点是红色的。

调整后

271

366

190

nil

251

357

402

395

530

443

nil

删除后

271

366

190

nil

251

357

530

402

395

443

nil

删除 z=786

nil

190

251

271

366

357

395

402

443

530

786

（2） 当前结点的兄弟结点是黑色的，而且兄弟结点的两个孩子结点都是黑色的。

上色

172

487

nil

237

632

514

746

删除后

172

487

nil

237

632

514

746

删除 z=62

62

172

237

487

514

632

746

（3） 当前结点的兄弟结点是黑色的，而且兄弟结点的左孩子是红色的，右孩子是黑色的当前结点是父结点的左子树的情况。
（4） 当前结点的兄弟结点是黑色的，而且兄弟结点的右孩子是红色的。
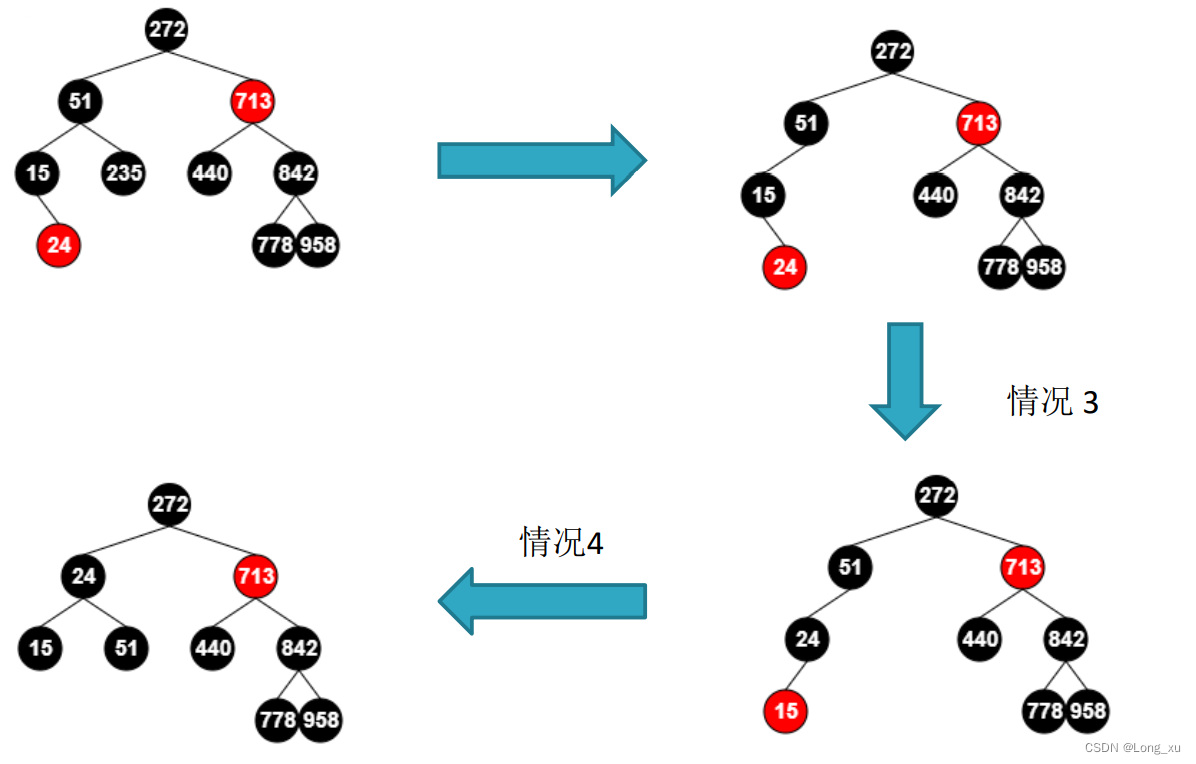
delete34

3.4.2、当前结点是父结点的右子树的情况

这种情况和【当前结点是父结点的左子树的情况】同理。

3.4.3、代码示例

/**********************红黑树删除 start***************************/
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
	while (x->node.left != T->nil) {
		x = x->node.left;
	}
	return x;
}

rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
	while (x->node.right != T->nil) {
		x = x->node.right;
	}
	return x;
}

rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x)
{
	rbtree_node *y = x->node.parent;
	if (x->node.right != T->nil)
	{
		return rbtree_mini(T, x->node.right);
	}

	
	while ((y != T->nil) && (x == y->node.right)) {
		x = y;
		y = y->node.parent;
	}
	return y;
}
//调整
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {

	while ((x != T->root) && (x->node.color == BLACK)) {
		if (x == x->node.parent->node.left) {

			rbtree_node *w = x->node.parent->node.right;
			if (w->node.color == RED) {
				w->node.color = BLACK;
				x->node.parent->node.color = RED;

				rbtree_left_rotate(T, x->node.parent);
				w = x->node.parent->node.right;
			}

			if ((w->node.left->node.color == BLACK) && (w->node.right->node.color == BLACK)) {
				w->node.color = RED;
				x = x->node.parent;
			}
			else {

				if (w->node.right->node.color == BLACK) {
					w->node.left->node.color = BLACK;
					w->node.color = RED;
					rbtree_right_rotate(T, w);
					w = x->node.parent->node.right;
				}

				w->node.color = x->node.parent->node.color;
				x->node.parent->node.color = BLACK;
				w->node.right->node.color = BLACK;
				rbtree_left_rotate(T, x->node.parent);

				x = T->root;
			}

		}
		else {

			rbtree_node *w = x->node.parent->node.left;
			if (w->node.color == RED) {
				w->node.color = BLACK;
				x->node.parent->node.color = RED;
				rbtree_right_rotate(T, x->node.parent);
				w = x->node.parent->node.left;
			}

			if ((w->node.left->node.color == BLACK) && (w->node.right->node.color == BLACK)) {
				w->node.color = RED;
				x = x->node.parent;
			}
			else {

				if (w->node.left->node.color == BLACK) {
					w->node.right->node.color = BLACK;
					w->node.color = RED;
					rbtree_left_rotate(T, w);
					w = x->node.parent->node.left;
				}

				w->node.color = x->node.parent->node.color;
				x->node.parent->node.color = BLACK;
				w->node.left->node.color = BLACK;
				rbtree_right_rotate(T, x->node.parent);

				x = T->root;
			}

		}
	}

	x->node.color = BLACK;
}

rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) 
{
	rbtree_node *y = T->nil;
	rbtree_node *x = T->nil;

	if ((z->node.left == T->nil) || (z->node.right == T->nil))
	{
		y = z;
	}
	else
	{
		y=rbtree_successor(T, z);
	}

	if (y->node.left != T->nil)
		x = y->node.left;
	else if (y->node.right != T->nil)
		x = y->node.right;


	x->node.parent = y->node.parent;
	if (y->node.parent == T->nil)
		T->root = x;
	else if (y == y->node.parent->node.left)
		y->node.parent->node.left = x;
	else
		y->node.parent->node.right = x;


	if (y != z)
	{
		z->key = y->key;
		z->value = y->value;
	}
	// 调整
	if (y->node.color == BLACK) {
		rbtree_delete_fixup(T, x);
	}

	return y;
}

/**********************红黑树删除 end***************************/

3.5、红黑树查找结点

/**********************红黑树查找 start***************************/
rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {

	rbtree_node *node = T->root;
	while (node != T->nil) {
		if (key < node->key) {
			node = node->node.left;
		}
		else if (key > node->key) {
			node = node->node.right;
		}
		else {
			return node;
		}
	}
	return T->nil;
}
/**********************红黑树查找 end***************************/

3.6、完整示例代码

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define RED				1
#define BLACK 			2

/**********************定义红黑树 start***************************/
typedef int KEY_TYPE;

// 红黑树模板，提高复用性
#define RBTREE_ENTRT(name,type)	\
	struct name{				\
		struct type *right;		\
		struct type *left;		\
		struct type *parent;	\
		unsigned char color;	\
	}

typedef struct _rbtree_node {
	KEY_TYPE key;
	void *value;
#if 0
	struct _rbtree_node *right;
	struct _rbtree_node *left;
	struct _rbtree_node *parent;

	unsigned char color;
#else
	RBTREE_ENTRT(, _rbtree_node) node;
	//RBTREE_ENTRT(, _rbtree_node) node2;
#endif
}rbtree_node;

typedef struct _rbtree {
	rbtree_node *root;
	rbtree_node *nil;
}rbtree;

/**********************定义红黑树 end***************************/

/**********************红黑树左旋 start***************************/
void rbtree_left_rotate(rbtree *T,rbtree_node *x)
{
	rbtree_node *y = x->node.right;
	// 1
	x->node.right = y->node.left;
	if (y->node.left != T->nil)
	{
		y->node.left->node.parent = x;
	}
	// 2
	y->node.parent = x->node.parent;
	if (x->node.parent == T->nil)
		T->root = y;
	else if (x == x->node.parent->node.left)
		x->node.parent->node.left = y;
	else
		x->node.parent->node.right = y;
	// 3
	y->node.left = x;
	x->node.parent = y;
}
/**********************红黑树左旋 end***************************/

/**********************红黑树右旋 start***************************/
/*
* x改为y，y改为x，右改为左，左改为右
*/
void rbtree_right_rotate(rbtree *T, rbtree_node *y)
{
	rbtree_node *x = y->node.left;
	// 1
	y->node.left = x->node.right;
	if (x->node.right != T->nil)
	{
		x->node.right->node.parent = y;
	}
	// 2
	x->node.parent = y->node.parent;
	if (y->node.parent == T->nil)
		T->root = x;
	else if (y == y->node.parent->node.right)
		y->node.parent->node.right = x;
	else
		y->node.parent->node.left = x;
	// 3
	x->node.right = y;
	y->node.parent = x;
}
/**********************红黑树右旋 end***************************/

/**********************红黑树插入 start***************************/
// 调整
void rbtree_insert_fixup(rbtree *T, rbtree_node *z)
{
	// 红黑树特性之一：如果一个结点是红的，则它的两个儿子是黑的
	while (z->node.parent->node.color == RED)
	{
		if (z->node.parent == z->node.parent->node.parent->node.left)
		{
			rbtree_node *y = z->node.parent->node.parent->node.right;
			if (y->node.color == RED)//叔父结点为红色
			{
				z->node.parent->node.color = BLACK;
				y->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;

				// 保证 Z 永远是红色，才能调整
				z = z->node.parent->node.parent;
			}
			else  //y==black
			{
				if (z == z->node.parent->node.right)
				{
					z = z->node.parent;
					rbtree_left_rotate(T, z);
				}
				z->node.parent->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;
				//祖父结点旋转
				rbtree_right_rotate(T, z->node.parent->node.parent);
			}
		}
		else
		{
			rbtree_node *y = z->node.parent->node.parent->node.left;
			if (y->node.color == RED)//叔父结点为红色
			{
				z->node.parent->node.color = BLACK;
				y->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;

				// 保证 Z 永远是红色，才能调整
				z = z->node.parent->node.parent;
			}
			else {
				if (z == z->node.parent->node.left) {
					z = z->node.parent;
					rbtree_right_rotate(T, z);
				}

				z->node.parent->node.color = BLACK;
				z->node.parent->node.parent->node.color = RED;
				rbtree_left_rotate(T, z->node.parent->node.parent);
			}
		}
	}
	T->root->node.color = BLACK;
}
// 插入到底部
void rbtree_insert(rbtree *T, rbtree_node *z)
{
	rbtree_node *y = T->nil;
	rbtree_node *x = T->root;
	while (x != T->nil)
	{
		y = x;
		if (z->key < x->key)
			x = x->node.left;
		else if (z->key > x->key)
			x = x->node.right;
		else
			return;
	}

	z->node.parent = y;
	if (y == T->nil)
		T->root = z;
	else {
		if (y->key > z->key)
			y->node.left = z;
		else
			y->node.right = z;
	}

	
	z->node.left = z->node.right = T->nil;
	z->node.color = RED;
	rbtree_insert_fixup(T, z);


}

/**********************红黑树插入 end***************************/

/**********************红黑树删除 start***************************/
rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
	while (x->node.left != T->nil) {
		x = x->node.left;
	}
	return x;
}

rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
	while (x->node.right != T->nil) {
		x = x->node.right;
	}
	return x;
}

rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x)
{
	rbtree_node *y = x->node.parent;
	if (x->node.right != T->nil)
	{
		return rbtree_mini(T, x->node.right);
	}

	
	while ((y != T->nil) && (x == y->node.right)) {
		x = y;
		y = y->node.parent;
	}
	return y;
}
//调整
void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {

	while ((x != T->root) && (x->node.color == BLACK)) {
		if (x == x->node.parent->node.left) {

			rbtree_node *w = x->node.parent->node.right;
			if (w->node.color == RED) {
				w->node.color = BLACK;
				x->node.parent->node.color = RED;

				rbtree_left_rotate(T, x->node.parent);
				w = x->node.parent->node.right;
			}

			if ((w->node.left->node.color == BLACK) && (w->node.right->node.color == BLACK)) {
				w->node.color = RED;
				x = x->node.parent;
			}
			else {

				if (w->node.right->node.color == BLACK) {
					w->node.left->node.color = BLACK;
					w->node.color = RED;
					rbtree_right_rotate(T, w);
					w = x->node.parent->node.right;
				}

				w->node.color = x->node.parent->node.color;
				x->node.parent->node.color = BLACK;
				w->node.right->node.color = BLACK;
				rbtree_left_rotate(T, x->node.parent);

				x = T->root;
			}

		}
		else {

			rbtree_node *w = x->node.parent->node.left;
			if (w->node.color == RED) {
				w->node.color = BLACK;
				x->node.parent->node.color = RED;
				rbtree_right_rotate(T, x->node.parent);
				w = x->node.parent->node.left;
			}

			if ((w->node.left->node.color == BLACK) && (w->node.right->node.color == BLACK)) {
				w->node.color = RED;
				x = x->node.parent;
			}
			else {

				if (w->node.left->node.color == BLACK) {
					w->node.right->node.color = BLACK;
					w->node.color = RED;
					rbtree_left_rotate(T, w);
					w = x->node.parent->node.left;
				}

				w->node.color = x->node.parent->node.color;
				x->node.parent->node.color = BLACK;
				w->node.left->node.color = BLACK;
				rbtree_right_rotate(T, x->node.parent);

				x = T->root;
			}

		}
	}

	x->node.color = BLACK;
}

rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) 
{
	rbtree_node *y = T->nil;
	rbtree_node *x = T->nil;

	if ((z->node.left == T->nil) || (z->node.right == T->nil))
	{
		y = z;
	}
	else
	{
		y=rbtree_successor(T, z);
	}

	if (y->node.left != T->nil)
		x = y->node.left;
	else if (y->node.right != T->nil)
		x = y->node.right;


	x->node.parent = y->node.parent;
	if (y->node.parent == T->nil)
		T->root = x;
	else if (y == y->node.parent->node.left)
		y->node.parent->node.left = x;
	else
		y->node.parent->node.right = x;


	if (y != z)
	{
		z->key = y->key;
		z->value = y->value;
	}
	// 调整
	if (y->node.color == BLACK) {
		rbtree_delete_fixup(T, x);
	}

	return y;
}

/**********************红黑树删除 end***************************/

/**********************红黑树查找 start***************************/
rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {

	rbtree_node *node = T->root;
	while (node != T->nil) {
		if (key < node->key) {
			node = node->node.left;
		}
		else if (key > node->key) {
			node = node->node.right;
		}
		else {
			return node;
		}
	}
	return T->nil;
}
/**********************红黑树查找 end***************************/


/**********************红黑树使用示例 start***************************/
// 遍历
void rbtree_traversal(rbtree *T, rbtree_node *node) {
	if (node != T->nil) {
		rbtree_traversal(T, node->node.left);
		printf("key:%d, color:%d\n", node->key, node->node.color);
		rbtree_traversal(T, node->node.right);
	}
}

int main() {

	int keyArray[20] = { 24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15 };

	rbtree *T = (rbtree *)malloc(sizeof(rbtree));
	if (T == NULL) {
		printf("malloc failed\n");
		return -1;
	}

	T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
	T->nil->node.color = BLACK;
	T->root = T->nil;

	rbtree_node *node = T->nil;
	int i = 0;
	for (i = 0; i < 20; i++) {
		node = (rbtree_node*)malloc(sizeof(rbtree_node));
		node->key = keyArray[i];
		node->value = NULL;

		rbtree_insert(T, node);

	}

	rbtree_traversal(T, T->root);
	printf("----------------------------------------\n");

	for (i = 0; i < 20; i++) {
		printf("search key = %d\n", keyArray[i]);
		rbtree_node *node = rbtree_search(T, keyArray[i]);
		printf("delete key = %d\n", node->key);
		rbtree_node *cur = rbtree_delete(T, node);
		free(cur);
		printf("show rbtree: \n");
		rbtree_traversal(T, T->root);
		printf("----------------------------------------\n");
	}
}

/**********************红黑树使用示例 end***************************/

四、使用红黑树示例


/**********************红黑树使用示例 start***************************/
// 遍历
void rbtree_traversal(rbtree *T, rbtree_node *node) {
	if (node != T->nil) {
		rbtree_traversal(T, node->node.left);
		printf("key:%d, color:%d\n", node->key, node->node.color);
		rbtree_traversal(T, node->node.right);
	}
}

int main() {

	int keyArray[20] = { 24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15 };

	rbtree *T = (rbtree *)malloc(sizeof(rbtree));
	if (T == NULL) {
		printf("malloc failed\n");
		return -1;
	}

	T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
	T->nil->node.color = BLACK;
	T->root = T->nil;

	rbtree_node *node = T->nil;
	int i = 0;
	for (i = 0; i < 20; i++) {
		node = (rbtree_node*)malloc(sizeof(rbtree_node));
		node->key = keyArray[i];
		node->value = NULL;

		rbtree_insert(T, node);

	}

	rbtree_traversal(T, T->root);
	printf("----------------------------------------\n");

	for (i = 0; i < 20; i++) {
		printf("search key = %d\n", keyArray[i]);
		rbtree_node *node = rbtree_search(T, keyArray[i]);
		printf("delete key = %d\n", node->key);
		rbtree_node *cur = rbtree_delete(T, node);
		free(cur);
		printf("show rbtree: \n");
		rbtree_traversal(T, T->root);
		printf("----------------------------------------\n");
	}
}

/**********************红黑树使用示例 end***************************/

五、总结

  1. 红黑树是一种二叉树，中序遍历绝对有序。当红黑树的性质被破环时，需要触发旋转，进行调整。

  2. 旋转有两种方式：左旋和右旋。

  3. 红黑树具有以下性质：
    （1）结点不是红色就是黑色；
    （2）每个叶子结点一定是黑色；
    （3）根节点一定是黑色；
    （4）如果一个结点是红的，则它的两个儿子是黑的；
    （5）对每个节点，从该结点到其子孙结点的所有路径上，都包含相同数目的黑结点；即黑高。这决定红黑树的平衡。

  4. 红黑数平衡主要是平衡黑高，即任一结点到其子叶子结点的黑色结点数量相同。红黑树的插入和删除会影响红黑树的性质，需要做调整。

在这里插入图片描述

版权声明：本文为Long_xu原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。