本人的很多知识都是从西瓜书中摘录来的,只是在这基础上加上一些自己理解
精度和错误率
精度和错误率一般是在分类问题中用来衡量模型的型能的评估指标,我们通常将分类错误的样本数占样本总数的比例称为错误率。所以比如有a个样本分错了,总样本数为m个样本。
那么错误率=a/m
而精度正是和错误率相反的一个性能指标,我们通常把1-a/m称为精度
误差分析
在训练过程中,我们一般会出现两种误差
1.第一种在训练集上出现的误差一般称为训练误差,或者说是经验误差。
2.在新样本上的误差我们一般称为泛化误差
过拟合和欠拟合
其实我觉得这个两个已经非常熟悉的概念。
但是还是在这里提一下吧
过拟合:简单来说就是在模型在训练集上表现很好,在新样本上泛化能力非常弱。为什么会出现这种情况呢,因为我们的模型学习了太多训练集中的特征,不光一些我们需要的特征还有一些噪声一起学习进去了。
欠拟合:欠拟合则是模型在训练集上的表现就不太好,一般我们认为出现欠拟合则是模型没有学习到一些该有的特征

这幅图可以很清楚的展示欠拟合和过拟合的基本概念
评估方法
这里我介绍西瓜书中给的三种评估方法
留出法
其实我们在初学过程中经常用到的就是留出法,留出法是什么意思呢。简单理解就是对数据进行分层抽样(有的时候还不是分层抽样)
其实像经常我个人在目前初学阶段,划分数据集都是直接用sklearn的train_test_split方法来按照比例划分。有的时候也是自己根据数据集的长度来按照比例划分。sklearn的方法可以设置随机数来打乱数据。但是针对于分类问题,关于数据分类这个问题还是有很多细节问题需要注意的
我们一般做的是将70%的数据集切分为训练集,30%的数据集切分为验证集
但是这里我有一个疑问,以二分类任务为例,若原样本数据正反例分布本就没有经过过采样或者欠采样而使得正反例数据数量相同,那么按照留出法进行分层采样后是不是划分出的数据不平衡性会更大呢?
留出法虽然是我们经常使用的方法,但是留出法一次划分训练后的结果是不稳定的,所以我们通常采用若干次随机划分,再对重复实现的结果求平均值
留出法有个非常明显的缺点:若划分出来的训练集样本数量相比于样本总量而言比较小,会导致验证集相比比较大,同时会影响模型学习整个样本数据的分布特征。
同理,若训练集样本数量接近样本总量,那么验证集的数量就相对而言比较小,模型的泛化能力就得不到很好的体现。
这个问题目前没有很好的解决方法,所以一般把2/3-4/5的数据集作为训练集,剩余的作为测试集
交叉验证法
交叉验证法是不同于留出法的一种数据划分方法
其思路是:首先将数据集划分为K个大小相近的互斥子集。并为保证每个子集尽量拟合数据分布趋势。划分子集时通常采用分层抽样的方式。
在划分数据集后,形成一个K-1个训练集和1个测试集,随后对数据进行K次训练,每次以其中1个为测试集,剩下的K-1个作为训练集。
最后对K个测试集进行测试并得到结果后取平均值
我们常用的K值有5,10,20。最常用的是10,所以通常称为10折交叉验证法

在交叉验证法中,为避免采用同一划分子集方式引起的误差,我们通常使用 P次不同划分子集方式
所以最后我们的方法是P次K折交叉验证
交叉验证法的特例是留一法,每次用1个样本作为测试集,其他作为训练集。这样就需要对数据训练K轮
交叉验证法的优缺点
优点:能极大保证训练集和样本总量的分布接近
缺点:若数据量过大,则需要非常大的计算量
自助法
交叉验证法同样存在与留出法一样的缺点,那么为了更加有效的避免这个缺点。自助法由此而生
假设有m个样本的训练集D,我们每次从D中随机取一个样本放入D’中,再将这个样本放回D中。重复m次,我们就得到了一个与D数量一样的数据集D‘
那么我们取每个样本抽到m次的概率
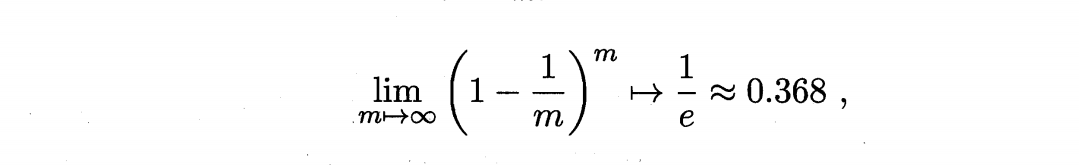
通过计算公式可以得知,每次划分数据集后,大概D中会有36.8%的数据未出现在D’中,这样我们以D‘为训练集,D-D’为测试集。这样的测试结果我们称为包外估计。
自助法的缺点:自助法会改变数据原有的分布
调参
调参其实是我们自己对模型中的一些参数进行修改,从而影响模型的效果