目录
一、什么是推荐算法
推荐算法(recommendation algorithm)是
机器学习和数据挖掘领域
的一个重要应用。它是指根据用户的历史行为、兴趣偏好、社交关系等因素,预测用户对商品、服务、新闻、音乐等信息的偏好,并向用户推荐相关的信息。推荐算法能够帮助用户发现感兴趣的内容,提升用户体验,同时也为商家和平台提供了一种个性化营销和服务的手段。
目前常用的推荐算法包括:
(1)基于
内容
的推荐算法:基于内容相似度计算,对物品进行推荐。例如推荐相似类型的电影、书籍、音乐等。
(2)
协同过滤推荐
算法:通过观察大量用户的历史行为数据,发现用户间可能存在的兴趣相似性,进而发现用户之间的关联关系,从而为每个用户推荐与其兴趣相关的物品。协同过滤算法可以分为基于用户的协同过滤算法和基于物品的协同过滤算法。
(3)
混合
推荐算法:结合多种推荐算法的优点,采用多层推荐策略,用于提高推荐的准确性和推广的效果。例如综合基于内容和协同过滤算法的混合推荐算法。
(4)基于
矩阵分解
的推荐算法:把用户-商品评分矩阵分解为多个低维度的矩阵,然后通过计算用户和商品向量的内积来预测评分和推荐物品。矩阵分解算法包括SVD分解、非负矩阵分解等。
除了以上常用的推荐算法之外,还有一些新的研究方向,例如
基于深度学习
的推荐算法、基于
知识图谱
的推荐算法等。
推荐算法在电商、社交媒体、新闻门户、视频音乐平台等应用场景中得到了广泛的应用。随着用户数据的增加和算法技术的发展,推荐算法将在未来得到更加广泛和深入的应用。
二、学习矩阵分解之前,先了解一下协同过滤
2.1 什么是协同过滤
协同过滤是一种常见的推荐系统算法,其基本思想是
利用用户行为来推荐物品
。具体地说,协同过滤通过分析用户历史行为数据,寻找其他用户或商品的相关性,然后根据这种相关性推荐未曾接触过的商品或者其他感兴趣的资源。
协同过滤算法可以分为基于
用户的协同过滤
和基于
物品的协同过滤
两种类型。
基于用户的协同过滤假设相似的用户在过去行为上具有相似的品味,因此给一个目标用户推荐和其邻居们常用的商品/内容。具体实现方式是通过计算用户之间的相似度,找到和目标用户最相似的 K 个用户,然后将这些用户喜欢的商品加权合并并推荐给目标用户。
基于物品的协同过滤则假设相似的商品最可能被一些用户共同购买或使用。首先计算物品之间的相似度,然后找到目标用户喜欢的物品集合,根据这个集合中的物品相似度推荐
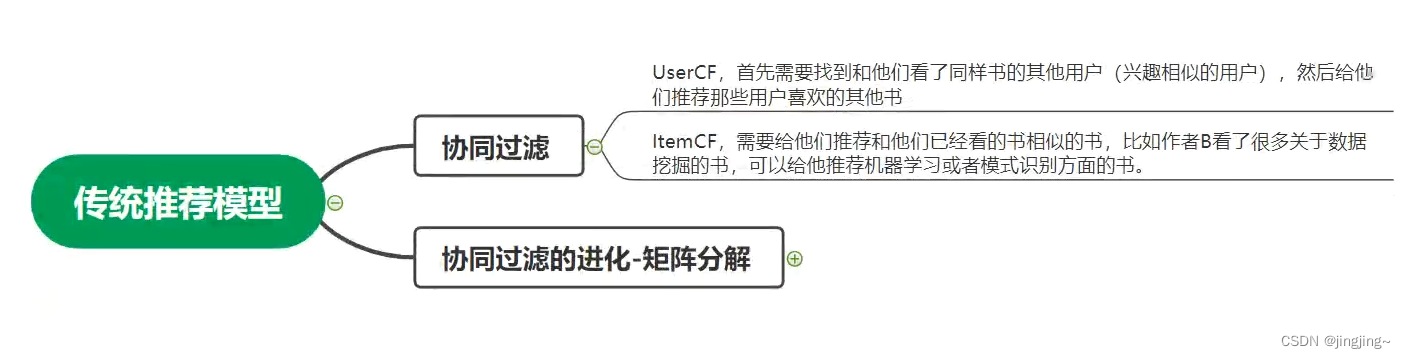
举例:

基于用户的协同过滤:比如小明阅读了《机器学习》和《线性代数》 那么 系统会根据小红阅读了《机器学习》从而推荐《线性代数》给小红
基于商品的协同过滤:比如小明喜欢数学(机器是不知道的),小明买了《线性代数》,《高等数学》,《离散数学》 现在要从《微积分》和《土木工程》里推荐一本给小明, 因此系统会推荐《微积分》给小明。
2.2 协同过滤存在的问题
协同过滤还存在一些问题,
矩阵分解相当于协同过滤的一个优化
比如:
协同过滤当中处理
稀疏矩阵
能力较弱:在一个稀疏阵中,不容易找到有用的信息
协同过滤当中,相似度矩阵维护
难度较大
:比如:用户相似度矩阵mxm,商品相似度矩阵nxn,在1亿×1亿的矩阵中,很难去计算。
三、矩阵分解
3.1什么是矩阵分解
矩阵分解(Matrix Factorization)是指把一个
复杂的矩阵分解成两个或多个简单的矩阵乘积的过程
。它是线性代数中的重要概念,并且在机器学习、推荐系统等领域中得到了广泛应用。
通常情况下,一个矩阵可以分解成多个简单矩阵的乘积形式,其中的一些简单矩阵也被称为矩阵的因子。常见的矩阵分解方法包括5种:
1.特征值分解:

2.奇异值分解(SVD)分解(Singular Value Decomposition):
任何一个实矩阵,其奇异值分解一定存在。




缺点:
(1)、传统的SVD分解,会要求原始矩阵是
稠密的
,而我们这里的这种矩阵一般情况下是
非常稀疏的
,如果想用奇异值分解,就必须对
缺失的元素进行填充
,而一旦补全,
空间复杂度就会非常高
,且
补的不一定对
。
(2)、然后就是SVD分解计算
复杂度
非常高,而我们的用户-物品矩阵非常大,所以基本上无法使用。
结论:
不适合用于解决大规模稀疏矩阵的矩阵分解问题
3.BasicSVD:下面详细讲解。
4.RSVD:RSVD是对BasicSVD的进一步优化,BasicSVD基础加上了
正则项 防止过拟合
。


RSVD的再进一步优化:加上一个偏置项

5.SVD++:再进一步改进
改进方向:(1)引入用户评过分的
历史物品
(2)物品之间的
某种关联
,会影响物品的评分(比如对逃学威龙1评分高的人,可能也会给逃学威龙2高评分)
(3)将这种关联对评分结果
产生的影响
,交给模型去学习
其中,
BasicSVD、RSVD和SVD++
已落实工业
矩阵分解在机器学习、推荐系统、计算机视觉等领域中有着广泛的应用,例如使用SVD分解进行推荐系统中的矩阵分解进行优化问题求解等。
3.2这里主要介绍BasicSVD算法
矩阵分解有好多种,主要是这5中
MF 是 Matrix Factorization 的缩写,即矩阵分解。在机器学习和推荐系统中,MF 是一种常见的矩阵分解算法,它通过将一个稀疏矩阵分解成两个低秩矩阵的乘积的形式来进行推荐。
具体地说,MF 算法将
用户-物品评分矩阵分解
成两个较小的矩阵,分别是用户矩阵和物品矩阵,矩阵的秩(rank)较小,可以看作对原始矩阵中的隐含特征进行了编码。而对于一个新用户或新商品,将其转化为向量表示,然后计算向量和低秩矩阵的乘积,就可以得到推荐评分。
MF算法背后的核心思想是信息隐藏,即假设用户-物品评分矩阵中存在着一些隐含的因素,例如用户的评分习惯、商品的属性等。MF算法可以通过分解矩阵来发现这些隐含因素,并基于这些因素进行推荐。
MF 算法通常采用
梯度下降
等优化算法来求解用户和物品矩阵,同时也可以加入
正则化
等技术来
避免过拟合和提高泛化能力
。
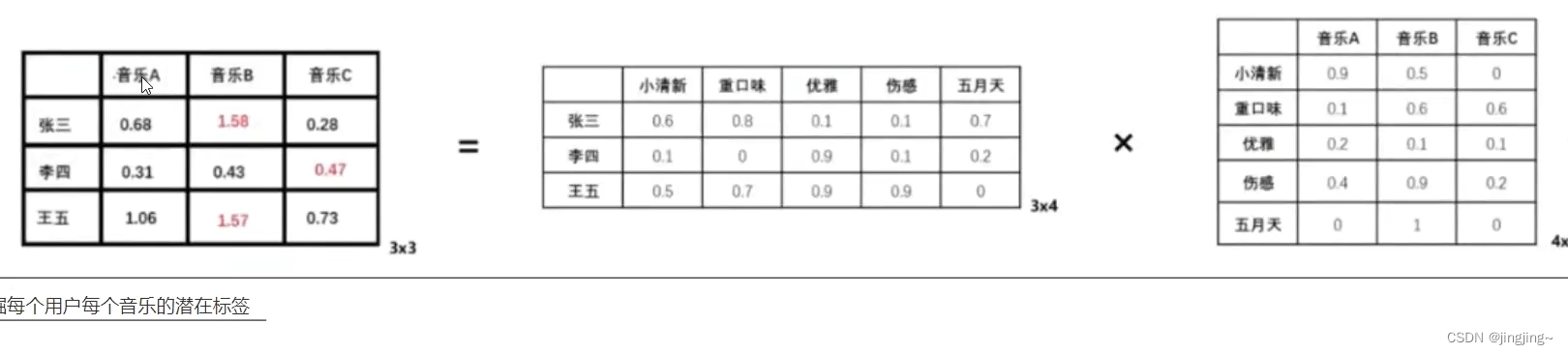
一个矩阵n×m 一定可以分解 n×k 和k×m的两个矩阵
比如
:
挖掘每个用户每个音乐的潜在标签
3×3=(3×4)×(4×3)
3.3实际应用
将矩阵分解问题转化为最优解问题,通过梯度下降进行优化。
首先,预测函数(
预测函数就是来求预测矩阵的
)
1.矩阵是
稀疏
的
2.隐含特征是不可解释的,不知道具体的含义,是需要模型自己去学的
3.
k代表
你所挖掘的
标签个数
,k越大,你的表达信息就越强
4.通过用户矩阵和物品矩阵,预测评分。公式:

其次,损失函数


然后,优化目标
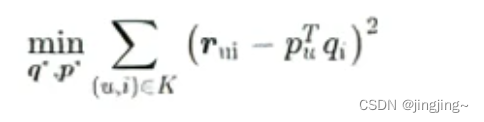
最后,梯度下降(求梯度和更新)
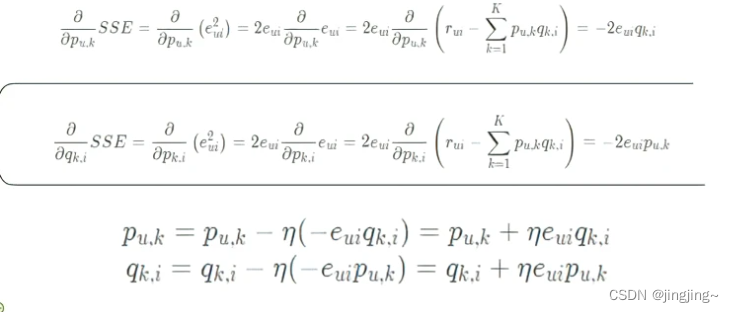
步骤:
1初始化参数矩阵P和Q
2通过两个隐向量乘积得到预测值pred
3根据label和pred计算损失
4通过梯度下降的方式更新两个隐向量的值
5未评过分的当做测试集,通过两个隐向量就可以得到测试集的label的值
6填充完矩阵
损失函数就是预测值和真实的差值:0.02,0.01
改变p和q的值,使差值无限小,梯度下降就是不断的更新迭代。
3.4代码实现
# -*- coding: utf-8 -*-
"""
Created on Sat Apr 22 15:12:05 2023
@author: Lenovo
"""
# !/usr/bin/env python
# encoding: utf-8
__author__ = 'Scarlett'
#矩阵分解在打分预估系统中得到了成熟的发展和应用
# from pylab import *
import matplotlib.pyplot as plt
from math import pow
import numpy
def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):
Q=Q.T # .T操作表示矩阵的转置
result=[]
for step in range(steps):
for i in range(len(R)):
for j in range(len(R[i])):
if R[i][j]>0:
eij=R[i][j]-numpy.dot(P[i,:],Q[:,j]) # .dot(P,Q) 表示矩阵内积
for k in range(K):
P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
eR=numpy.dot(P,Q)
e=0
for i in range(len(R)):
for j in range(len(R[i])):
if R[i][j]>0:
e=e+pow(R[i][j]-numpy.dot(P[i,:],Q[:,j]),2)
for k in range(K):
e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
result.append(e)
if e<0.001:
break
return P,Q.T,result
if __name__ == '__main__':
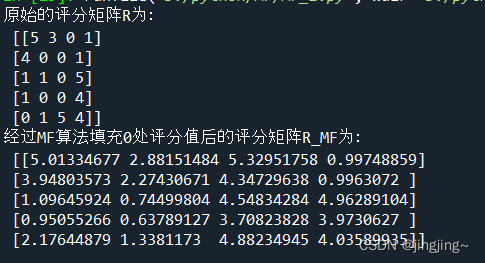
R=[
[5,3,0,1],
[4,0,0,1],
[1,1,0,5],
[1,0,0,4],
[0,1,5,4]
]
R=numpy.array(R)
N=len(R)
M=len(R[0])
K=2
P=numpy.random.rand(N,K) #随机生成一个 N行 K列的矩阵
Q=numpy.random.rand(M,K) #随机生成一个 M行 K列的矩阵
nP,nQ,result=matrix_factorization(R,P,Q,K)
print("原始的评分矩阵R为:\n",R)
R_MF=numpy.dot(nP,nQ.T)
print("经过MF算法填充0处评分值后的评分矩阵R_MF为:\n",R_MF)
#-------------损失函数的收敛曲线图---------------
n=len(result)
x=range(n)
plt.plot(x,result,color='r',linewidth=3)
plt.title("Convergence curve")
plt.xlabel("generation")
plt.ylabel("loss")
plt.show()运行结果:
损失函数图:

# -*- coding: utf-8 -*-
"""
Created on Fri Apr 21 18:13:42 2023
@author: Lenovo
"""
import random
import math
import numpy as np
class SVD(object):
def __init__(self,rating_data,F,alpha=0.1,lmbd=0.1,max_iter=1000):
#F 为隐因子个数
#lmbd 为正则化
# alpha 为学习率
# max_iter 最大迭代次数
self.F=F # 隐因子个数
self.P=dict() #R=PQ^T,代码中的Q相当于转置 创建空的P矩阵
self.Q=dict() #创建空的Q矩阵 dict () 函数用于创建一个字典
self.alpha=alpha #学习率
self.lmbd=lmbd #正则化 是机器学习中对原始损失函数引入额外信息,以防止过拟合提交准确
self.max_iter=max_iter #迭代次数
self.rating_data=rating_data#读入数据
#随机初始化矩阵P和Q
#user表示A,B,C rates表示
for user, rates in self.rating_data:
self.P[user] = [random.random() / math.sqrt(self.F)
for x in range(self.F)]
#print(self.rating_data)
#print(rates)
#print(self.P)
#print(user)
for item, _ in rates:
if item not in self.Q:
self.Q[item]=[random.random() / math.sqrt(self.F)
for x in range(self.F)]
#print(self.Q)
def train(self):
"""
随机梯度下降法训练参数P和Q
: return :
"""
for step in range(self.max_iter):#遍历次数max_iter
for user, rates in self.rating_data:
for item, rui in rates:
hat_rui = self.predict(user,item)#预测得分
err_ui = rui - hat_rui#计算误差
for f in range(self.F):#梯度下降更新
self.P[user][f] += self.alpha *(err_ui * self.Q[item][f] - self.lmbd * self.P[user][f])
self.Q[item][f] += self.alpha *(err_ui * self.P[user][f]- self.lmbd * self.Q[item][f])
self.alpha*= 0.9#每次迭代步长要逐步缩小
def predict(self, user, item):
#预测用户user对物品item的评分
return sum(self.P[user][f] *self.Q[item][f] for f in range(self.F))
if __name__ == '__main__':
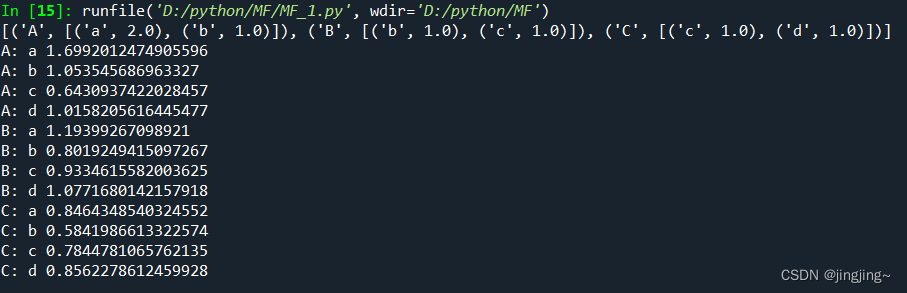
#用户有A BC,物品有abc d
rating_data = list()#定义列表
rate_A =[('a',2.0),('b',1.0)]
rating_data.append(('A', rate_A)) #在A的列表末尾添加新的对象
rate_B=[('b',1.0),('c',1.0)]
rating_data.append(('B', rate_B))
rate_C= [('c', 1.0),( 'd', 1.0)]
rating_data.append(('C',rate_C))
#print(1en(rating_data))
print(rating_data)
svd = SVD(rating_data,2)#2表示隐因子个数
svd.train()
for item in ['a', 'b', 'c', 'd']:
print("A:",item, svd.predict('A', item)) #计算用户A对各个物品的喜好程度
for item in ['a', 'b', 'c', 'd']:
print("B:",item, svd.predict('B', item)) #计算用户B对各个物品的喜好程度
for item in ['a', 'b', 'c', 'd']:
print("C:",item, svd.predict('C', item)) #计算用户C对各个物品的喜好程度
运行结果:
加了
正则项
整理:
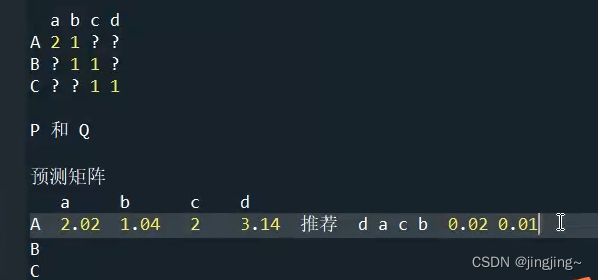
原矩阵: 可分解为PQ两个矩阵 P:3X2 Q:4X2 转置是2X4
a b c d
A 2 1 ? ?
B ? 1 1 ?
C ? ? 1 1
预测矩阵:
a b c d
A 1.699 1.053 0.643 1.015
B 1.193 0.801 0.933 1.077
C 0.846 0.584 0.784 0.856
没加
正则项

预测矩阵:
a b c d
A 1.820 1.106 1.275 1.272
B 1.195 0.903 1.059 0.894
C 1.251 0.830 0.964 0.897
在这个矩阵分解过程中变化不是很大。
四、总结分析矩阵分解的优缺点
主要是与协同过滤进行对比(
优点
):
(1)泛用性强,在一定程度上解决了稀疏矩阵的问题
(2)空间复杂度低
比如:用户相似度矩阵:nXn 1亿X1亿
商品:mXm 100亿X100亿
矩阵分解 nXK KXm
1000X(100亿+1亿)
(3)更好的扩展和灵活性
局限性
:
缺乏历史交互信息
与协同过滤一样,无法利用用户特征、物品特征、上下文特征
参考文献
[EB/OL].https://www.bilibili.com/video/BV1P44y1s7T2/?spm_id_from=333.999.0.0&vd_source=ce838d56b689e47d2bdd968af2d91d20