
这篇基主要覆盖官方视频的第1讲和第2讲,第12讲,和 AN5021的一小部分。主要介绍旋转,旋转矩阵和参考坐标系的知识
描述三维空间物体状态需要6维坐标
想要描述一个刚体在空间中的状态(姿态+位置)至少需要6个数字,三轴坐标+三个角度:
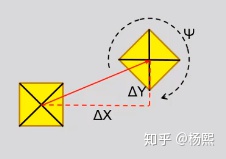

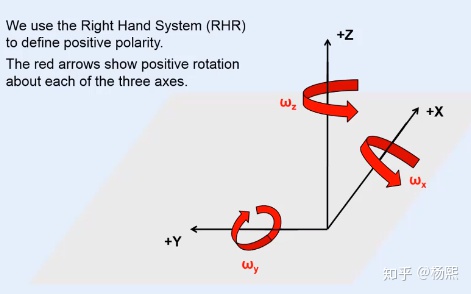
我们使用右手系
我们全部采用右手系,啥叫右手系呢,分两个小知识点:
- 拿出右手,三个指头分别指向XYZ
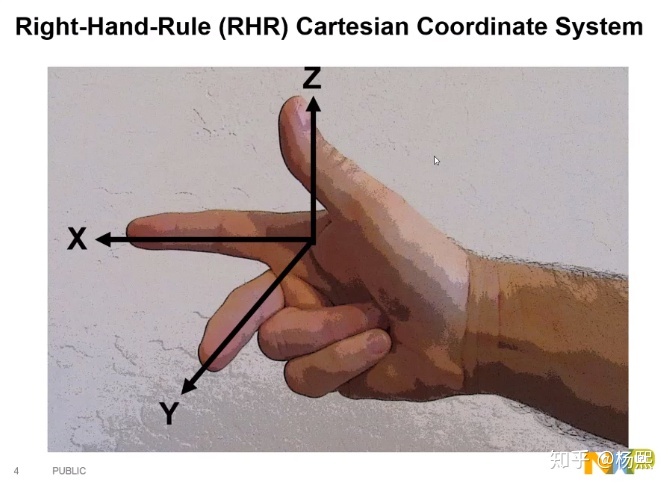
- 角速度: 大拇指指向轴向,四指转向即为角速度正方向:

常用参考坐标系
- NED( XYZ分别指向 North-East-Down,北东地)
- ENU( XYZ 分别指向 East-North-Up 东北天)
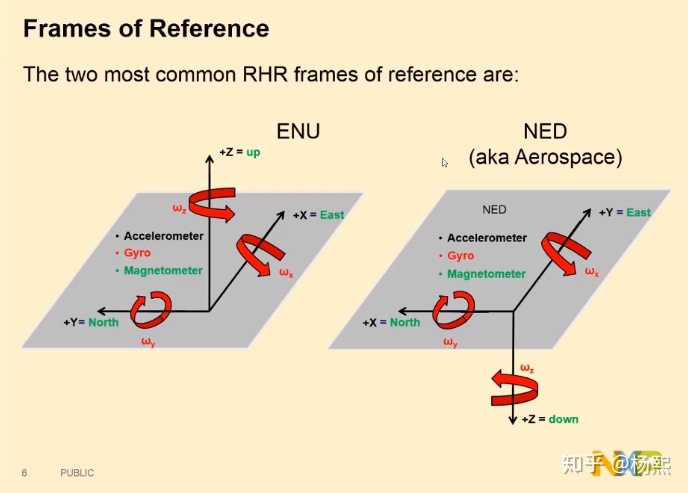
本笔记大部分以NED为准
姿态的数学表示概览
下面介绍描述姿态的部分:有以下几种数学表示来描述刚体在3维空间的姿态:
- 欧拉角: (Roll, Pitch, Yaw) 有顺序欧拉死锁的问题, 计算起来也比较复杂
- 旋转矩阵: 用一个3×3矩阵来描述物体的姿态,占内存大,计算量大
- 轴角对: 用一个轴(x,y,z)和一个角度来描述物体的姿态,直观,但是不好用,计算起来不方便
- 四元数: 类似轴角对,也是用4个数字 比轴角对更抽象一些。但是各种数学性质良好啊。大家一般计算都用这个
欧拉角(Euler Angles)
欧拉角用三个角度表示一个物体运动的姿态,分别叫Roll,Pitch,Yaw, 注意欧拉角有旋转顺讯这么一说,即先转什么轴,再转什么轴,最后转什么轴。说欧拉角必须讲顺序
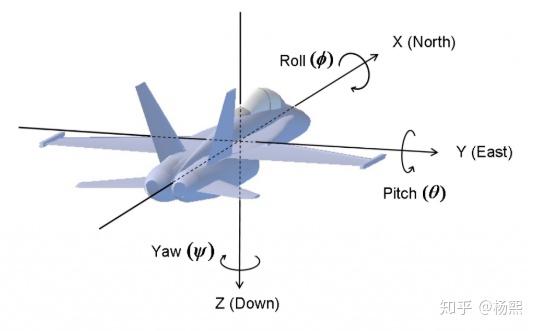
总结:定义机头方向为X轴,翅膀方向为Y,然后用右手定则确定Z方向.
-
绕 Z 轴方向旋转: 航向角yawpsi
范围: -180° – 180°
-
绕 Y 轴方向旋转: 俯仰角pitchtheta
范围: -90°-90°
-
绕 X 轴方向旋转:横滚角rollphi
范围: -180°-180°
- 欧拉角很直观,三个图,不怎么用文字就可以说明了。但欧拉角两个致命缺点(特点):
-
欧拉角有顺序这么一说: 先转哪个轴,再转哪个轴,最后转哪个轴。 不同的转法最后的欧拉角的值也不一样(这也是为什么网上的四元数转欧拉角公式不统一的原因),最流氓的就是给一个四元数转欧拉角公式,而不告诉你欧拉角的旋转顺序是啥。额。所以,记住:
说到欧拉角,不仅仅是三个值,一定还要跟上说你的旋转顺序是啥
。

- 著名的欧拉死锁问题:
任何只用三个数来表示刚体姿态的表述方法都会存在死锁问题. 这是数学问题,无法避免。可以通过四元数或者更多数字的表示方法(如DCM)来解决。

轴角对(Aixs-Angle) 和等效旋转矢量(Rotation Vector)
绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。这是除了欧拉角外,最直观的一种表述方法
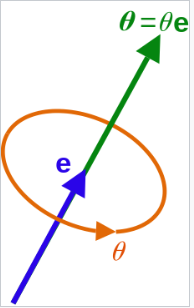
例:
绕旋转轴为
,旋转90°可以表示为如下形式(实际上就是绕着Z轴转90度)
旋转矢量:
旋转矢量和轴角对非常类似,轴角对使用4个数来描述姿态。根据欧拉定理,使用三个数就可以完整的描述姿态,所以轴角对存在冗余。旋转矢量实际上就是把轴角对进行”压缩”。怎么压缩呢? 就是把轴进行单位化,把角乘到轴向量上:
设把轴角对的轴进行单位化为
,转过的角度为
。那么定义旋转矢量为:
。旋转矢量是把轴角对进行压缩,使用三个数来表示旋转
旋转矩阵
让我们来研究一下坐标系的旋转:先简单的针对二维平面:
假设有一个在B系(body,物体坐标系)上的向量A,那么在N系下(E系,地球系,固定系)下,A是怎么表示的呢?
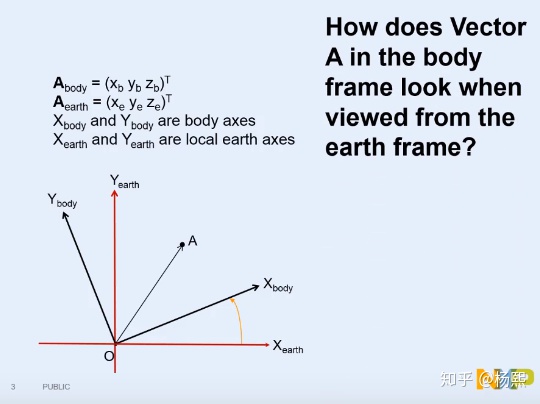
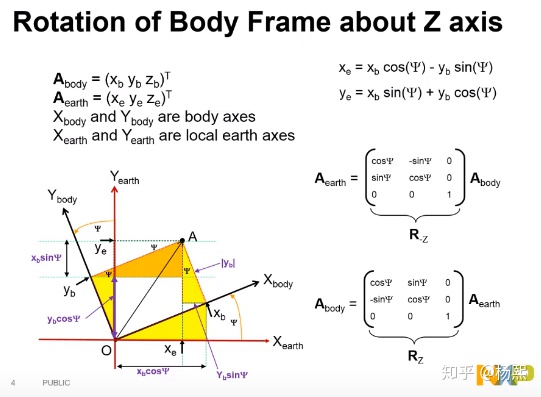
答案就是:
上面这个二维的例子也可以看做三维空间里的旋转,只不过X,Y不转,只绕Z轴旋转
:
绕Z轴旋转公式:
反之可表示为:
注意:(旋转矩阵是正交矩阵,转置即为取逆)
由此,我们可以推广出三维空间绕三个轴的旋转公式:(注意都是从 N系到B系)
绕X轴旋转:
绕Y轴旋转:
绕Z轴旋转:
把这三个旋转组合起来:可以得到欧拉角到旋转矩阵的转换公式:
(假设NED坐标系):
注意,这个公式是针对NED,旋转顺序先Z再Y再X的顺序来旋转,如果旋转顺序不是这个,这个公式也就不一样了
旋转矩阵小角度近似
当小角度近似时,有:
, 其中
代表三维向量的反对称矩阵:
旋转矩阵求导
我们在对小角度近似矩阵C对求时间求导,可得:
,其中
是什么?它是三轴陀螺仪的角速度啊!是可以从传感器里读出来的值!这样陀螺仪的数据就和姿态联系上了。天啊!陀螺仪数据组成插积矩阵然后进行积分就可以得到姿态!
关于坐标系变换 多讲一点,引申一下
如果有悟性的话,可以悟道:
- 旋转矩阵可以把一个B系的向量转到N系,或者反之。
- 旋转矩阵和陀螺输出有关系,而且是微分的关系
-
如果
或者
(第一个是重力! 第二是地磁场!)其中
是地磁倾角。 这样我们就可以根据这两个在N系下不变的向量来制作一个所谓”虚拟陀螺仪”的东西了!
参考(除NXP传感器融合资料外)
- Paul D.Groves GNSS与惯性及多传感器组合导航系统原理