博客

DCT变换和DFT变换

1：DFT变换

这里我只谈论二维的DFT变换，有关一维的DFT，请查看一下博客，里面有详细介绍：

https://blog.csdn.net/IMWTJ123/article/details/79831242

根据上面的公式，我们可以得到对应的离散傅里叶变换呃代码，下面是matlab版本的代码，和公式(12)是一一对应的，时间复杂度为（MN)^2，通常记成N^4，因此对于一个512*512的图片来说，计算量就已经很大了，更不用说别的高分辨率图像了，下面的代码输入block_struct是为了方便做blockproc，如果直接将图像的值赋给f就可以直接做DFT：

function F =  dft2(block_struct)

f=block_struct.data;
[M, N] = size(f);
F = zeros(M,N);

for k = 0:M-1
    for l = 0:N-1
        F(k+1,l+1) = dft_atomic_sum(f,k,l,M,N);
    end
end

%% computing a core of DFT2
function F_kl = dft_atomic_sum(f,k,l,M,N)

F_kl = 0;

for m=0:M-1
    for n=0:N-1
        F_kl = F_kl + f(m+1,n+1)*exp(-i*2*pi*( k*m/M   + l*n/N) );        
    end
end

因此，常用的方法就是先将图像划分为8*8的块，然后对每个块执行DFT变换：

fun_dft = @(block_struct) dft2(block_struct);
after_DFT=blockproc(Y,[8,8],fun_dft);

这样的时间复杂度就降低了很多，变成了O（8*8*block_num），其中block_num就是块的个数，因此现在常用的FFT算法，该算法的介绍很多，本文主要介绍原始DFT，对FFT感兴趣的可以查阅相关资料。

2：IDFT

IDFT为离散傅里叶变换的逆变换，公式如下;

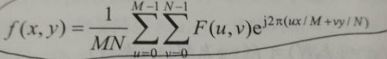
相应的代码如下，是根据DFT2改编的：

function F =  idft2(block_struct)

f=block_struct.data;
[M, N] = size(f);
F = zeros(M,N);

for k = 0:M-1
    for l = 0:N-1
        F(k+1,l+1) = idft_atomic_sum(f,k,l,M,N);
    end
end

%% computing a core of DFT2
function F_kl = idft_atomic_sum(f,k,l,M,N)

F_kl = 0;

for m=0:M-1
    for n=0:N-1
        F_kl = F_kl + f(m+1,n+1)*exp(i*2*pi*(k*m/M+l*n/N));        
    end
end

F_kl = 1/N * 1/M * F_kl ;

同样需要对图像的8*8的块进行IDFT，代码如下：

fun_idft=@(block_struct) idft2(block_struct);
after_iDFT=blockproc(after_DFT,[8,8],fun_idft);
after_iDFT=abs(after_iDFT);

可以试验一下，先进行DFT，然后进行IDFT，可以无损的恢复回来：

img=magic(8)
block_struct.data=img
after_dft=dft2(block_struct)
after_inverse_dft=abs(idft2(after_dft))
after_inverse_dft==img

3: DCT

同样的，我只对二维的DCT变换做一些介绍，一维的DCT以及相应理论可以查看下面这篇论文：

https://blog.csdn.net/qq_20613513/article/details/78744101

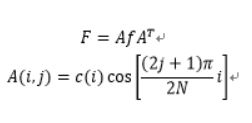
产生DCT变换矩阵A的代码如下：

N=8;
A=zeros(N);
 for i=0:N-1
    for j=0:N-1
        if i==0
            a=sqrt(1/N);
        else
            a=sqrt(2/N);
        end            
        A(i+1,j+1)=a*cos(pi*(2*j+1)*i/(2*N));
    end
 end

同理，对8*8块进行DCT变换的代码如下，如果不想使用8*8分块进行DCT，那么需要产生一个N*N大小的DCT变换矩阵A，然后使用F=AfA’计算：

fun = @(block_struct) A*(block_struct.data)*A';
after_DCT=blockproc(image,[8,8],fun);

4：IDCT

离散余弦变换的逆变换，逆变换非常简单，只需要令f=A’FA就可以了：

fun2 = @(block_struct) A'*(block_struct.data)*A;
inverse_DCT=blockproc(after_zigzag,[8,8],fun2);

5：实验结果

中间的DCT结果是我使用zigzag保留前16个系数，其余都置零得到的结果：

下面是使用DFT变换之后的结果，第二幅图是使用abs(after_dft)得到的频谱图，第三幅图是使用angle(after_dft)得到的相位图，IDFT是逆变换之后的得到的恢复的图像。