
2022年春季学期
计算学部《软件构造》课程
**Lab 2实验报告
**
| 姓名 | 李启明 |
|---|---|
| 学号 | 120L021920 |
| 班号 | 2003006 |
| 电子邮件 | 1094583745@qq.com |
| 手机号码 | 15645157396 |
目录
3.1.1 Get the code and prepare Git repository
3.1.2 Problem 1: Test Graph <String>
3.1.3 Problem 2: Implement Graph <String>
3.1.3.1 Implement ConcreteEdgesGraph
3.1.3.2 Implement ConcreteVerticesGraph
3.1.4 Problem 3: Implement generic Graph<L>
3.1.4.1 Make the implementations generic
3.1.4.2 Implement Graph.empty()
3.2 Re-implement the Social Network in Lab1
实验目标概述
本次实验训练抽象数据类型(ADT)的设计、规约、测试,并使用面向对象
编程(OOP)技术实现 ADT。具体来说:
⚫针对给定的应用问题,从问题描述中识别所需的 ADT;
⚫设计 ADT 规约(pre-condition、post-condition)并评估规约的质量;
⚫根据 ADT 的规约设计测试用例;
⚫ADT 的泛型化;
⚫根据规约设计 ADT 的多种不同的实现;针对每种实现,设计其表示
(representation)、表示不变性(rep invariant)、抽象过程(abstraction
function)
⚫使用 OOP 实现 ADT,并判定表示不变性是否违反、各实现是否存在表
示泄露(rep exposure);
⚫测试 ADT 的实现并评估测试的覆盖度;
⚫使用 ADT 及其实现,为应用问题开发程序;
⚫在测试代码中,能够写出 testing strategy 并据此设计测试用例。
实验环境配置
简要陈述你配置本次实验所需环境的过程,必要时可以给出屏幕截图。
特别是要记录配置过程中遇到的问题和困难,以及如何解决的。
在这里给出你的GitHub Lab2仓库的URL地址(Lab2-学号)。
实验过程
请仔细对照实验手册,针对两个问题中的每一项任务,在下面各节中记录你的实验过程、阐述你的设计思路和问题求解思路,可辅之以示意图或关键源代码加以说明(但千万不要把你的源代码全部粘贴过来!)。
Poetic Walks
这个实验的主要目的是测试 ADT 的规约设计和 ADT 的多种不同的实现,并练习 TDD 测试优先编程的编程习,在后面练习 ADT 的泛型化。
Get the code and prepare Git repository
如何从GitHub获取该任务的代码、在本地创建git仓库、使用git管理本地开发。
Problem 1: Test Graph <String>
首先,我们只需测试(而后实现)带有String类型顶点标签的图。稍后,我们将扩展到其他类型标签。
为了在多种Graph接口的实现上兼容运行我们的测试,以下给出测试步骤:
测试策略与对Graph.empty()静态方法的测试在GraphStaicTest.java中。由于该方法为静态方法,将只有一种实现方式,并且我们只需要运行一次测试。该部分测试已经给出,我们可以改变或添加内容,或不做改变。
在GarphInstanceTest.java中,对实例方法的测试使用emptyInstance()方法创建一个空图,并对Graph接口中的各个方法进行输入划分并测试。其中对起始空点的测试testInitialVerticesEmpty()已经在GraphInstancesTest.java文件中给出。
对Graph接口中方法的测试策略大致可以阐述如下:
1) 将图划分为空图和非空图
2) 将图中用于测试的顶点分为两组,一组已经存在于图中,另一组不存在于图中。
3) 将图中用于测试的边根据端点在图中的存在性和边权的性质分组,根据端点存在性分为“两点存在”、“只有一点存在”和“两点不存在”三组;根据边权的性质将边分为“边权为0”和“边权为正整数”两组;
4) 测试方法的实现调用Graph接口提供的add(), remove(), set, sources, targets, vertices()等方法充分覆盖对输入集的划分。
Problem 2: Implement Graph <String>
首先查看了一下Graph的代码,这里边已经写好了一些空的方法,需要我们具体的用边和点来表示Graph,来实现他给我们提供的Graph接口。从这里开始,实验开始要求我们对程序设计的规范化:要求注明AF、RI以及避免产生rep exposure的方法的信息,要求设计出合理的检查函数checkRep(),要求设计出合理的构造器、观察器,要求重写equals方法、hashCode方法以及toString方法。这里简单介绍以下相关概念的理解:
**Abstraction function:**抽象函数(AF),可以看作我们设计的类的成员变量到这些变量所表示的抽象概念的映射。换言之就是我们如何用自己声明的具体变量去表示求解问题时的抽象对象,在本实验中即图的信息:怎样表示这个图包含了哪些顶点与哪些边;
**Representation invariant:**表示不变量(RI),所有值的一个包含所有合法的值的一个子集,也可以看作对合法信息的一种描述:对于每个变量,怎样的数据(参数)是合法的,怎样的数据(参数)是不合法的;
**Safety from rep exposure:**防止表示泄露,在代码提供至客户方时,为防止关键信息被修改导致程序崩溃或产生bug,需要对关键数据进行保护,最典型的方法就是使用私有类型变量以及不可变类型变量;
**hashCode与equals:**每一个具体对象在java中都自带有hashCode与equals方法,前者用于对对象进行查找,而后者用于对对象进行对比。在实验中,如果需要使用到这两个方法,则需要对其进行重写。
Implement ConcreteEdgesGraph
这一部分要求我们使用边来实现Graph结构
-
首先我们实现Edge类
先给出三个必要的Field,其中分别代表源点,目标点,和权值。
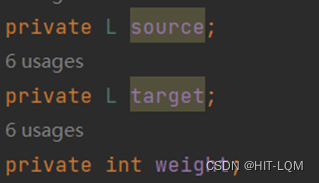
然后我们设计规约

后续可以依据次规约来设计checkRep函数;
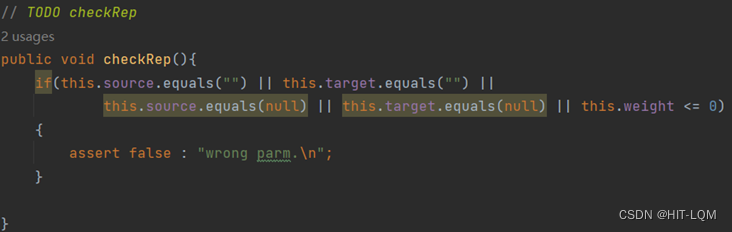
接下来编写Edge类的constructor
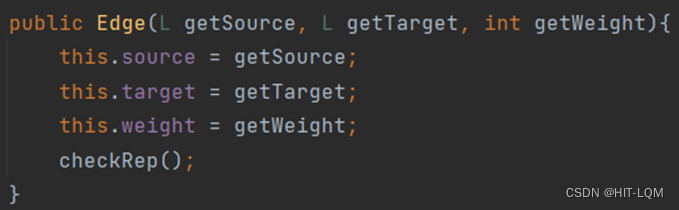
然后依次实现Edge类的方法:
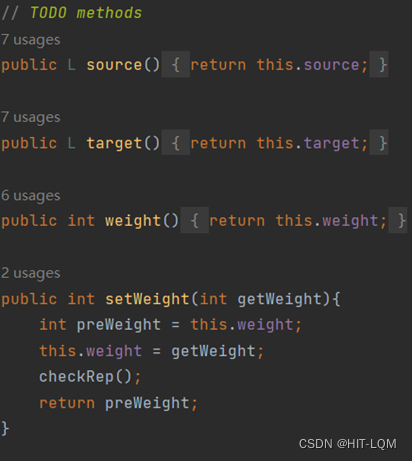
在重写equals的方法时,也要同时重写hashCode方法
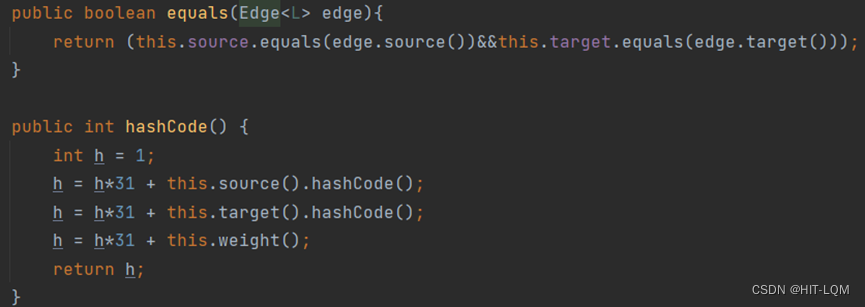
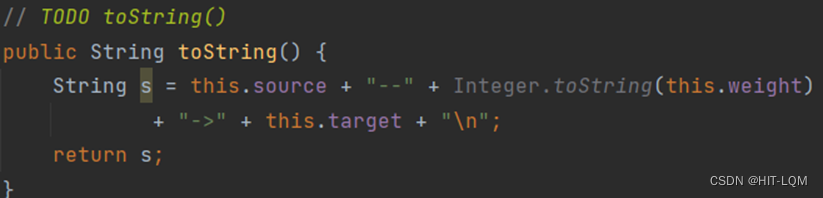
最终我们按照要求来实现打印函数toString
完成设计后,我们对Edge类进行了测试,其基本思想请见Problem1。测试验证表明,我们实现了上述要求的基本功能。
-
接下来我们继续实现concrete
首先定义点vertices和边edges
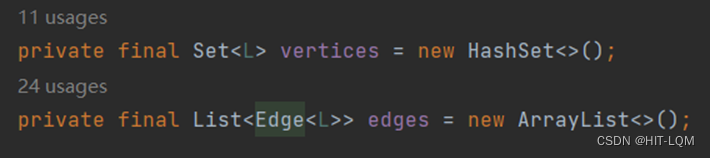
然后给出规约

构造性方法,只需定义一个空图即可
随后我们实现checkRep函数
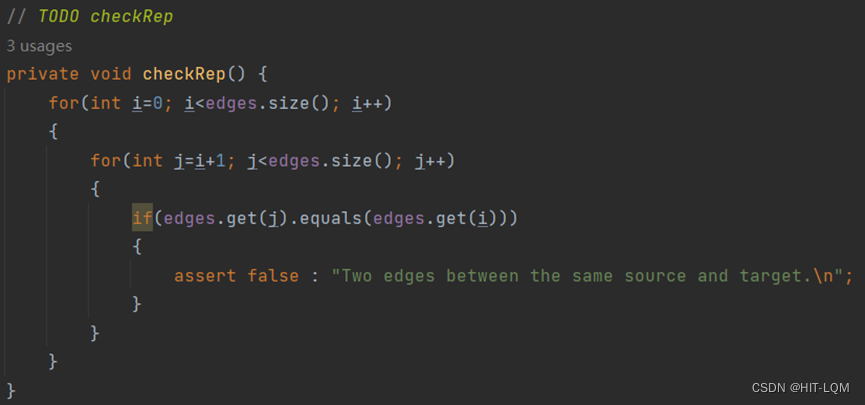
随后我们实现ConcreteEdegsGraph类的其他方法:
public boolean add(L vertex):
根据函数规约,只需遍历vertices集合,查找有无与点vertex相同的点即可。若存在,则返回false;不存在,则在vertices集合中添加点vertex,然后返回true;
public int set(L source, L target, int weight):
根据函数规约,该方法主要分三种操作:修改已有的边,移除已有的边,添加新的边。因此,先遍历edges集合,若存在对应端点的边,则根据weight的值进行修改权值/删除该边的操作,并返回原权值;若不存在对应的边,则判断weight的值是否为0,若不为0,则添加该边至edges集合中,并将不存在于vertices集合中的点添加到vertices集合中,然后返回0,否则不做任何操作,直接返回0。
public boolean remove(L vertex):
根据函数规约,先将edges集合中所有以vertex为源点/终点的边全部移除,然后根据hashSet类中remove()方法的定义及返回值,函数只需返回vertices.remove(vertex)即可。
public Set<L> vertices():
根据函数规约,这里只需要返回由图的顶点构成的集合即可。注意到保证数据信息不泄露,需要返回一个由vertices集合复制的新集合。
public Map<L, Integer> sources(L target):
根据函数规约,函数需要返回所有直接指向target的点以及与之对应的边的权值。这里规定了返回值的类型为Map,故只需要生成一个Map然后遍历edges集合寻找所有以target为终点的边并将其源点作为键名、权值作为键值添加到新生成的Map中,最后返回该Map即可。
public Map<L, Integer> targets(L source):
根据函数规约,函数需要返回所有source直接指向的点以及与之对应的边的权值。这里规定了返回值的类型为Map,故只需要生成一个Map然后遍历edges集合寻找所有以source为源点的边并将其终点作为键名、权值作为键值添加到新生成的Map中,最后返回该Map即可。
public String toString():
函数需要将图的所有信息打印出来,即所有的点与边的信息。故先将所有的点的名称打印出来,随后遍历edges集合,循环调用Edge类的toString方法即可。
最后对上述的类设计测试,以此检验上述功能
Implement ConcreteVerticesGraph
和上一问比较类似,这一问要求我们用点来实现Graph接口,同时我们应该首先实现Vertex类,在根据其实现ConcreteVerticesGraph类。
-
首先,我们设计Vertex类
Vertex成员变量应当包含指向它的点的集合和它指向的点的集合,用Map键值对来保存上述信息,点的名字为键值,形成的边的权值作为键值。由于我们需要为每个Vertex变量定义特定的标识来区分不同的变量,因此增加L类型的变量name作为标记。
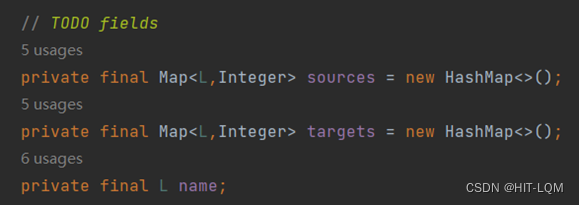
然后我们设计规约
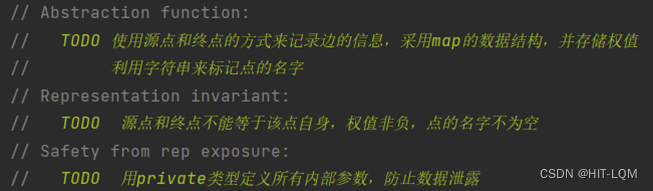
给出构造性方法
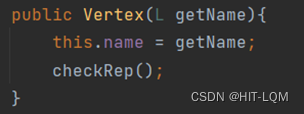
根据规约来设计checkRep方法
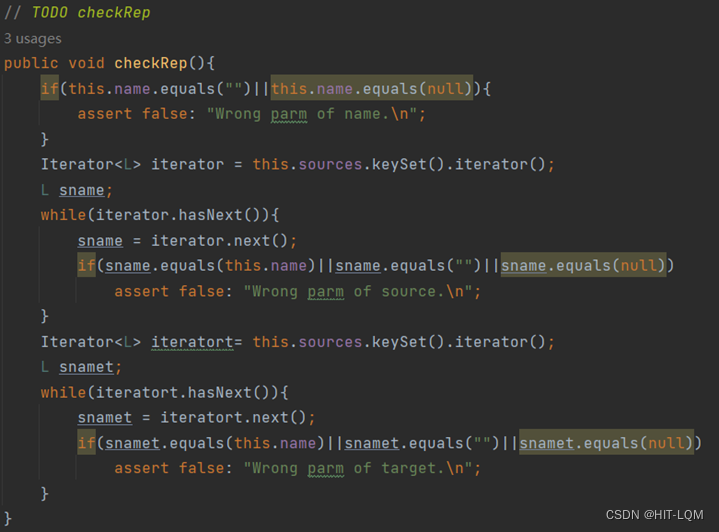
然后设计Vertex类中剩余的各个方法:
完成Vertex类中各个变量的观察器:返回点的名称、源点集、终点集;
修改原点集函数public int setSources(L source, int weight):根据Map类中remove()方法的返回值,若输入权值weight为0,直接使用remove()函数移除Map中键名为source的点,若source点存在,返回值为其原键值(int型),否则返回null。同理,根据Map类中put()方法的返回值,若输入权值weight不为0,直接使用put()函数修改Map中键名为source的点对应的键值为weight,若source点存在,返回值为其原键值(int型),否则返回null。定义Integer型变量pre记录两种分支下得到的返回值,若为null则返回0,否则返回对应int型变量。
修改原点集函数public int setTargets(L target, int weight):根据Map类中remove()方法的返回值,若输入权值weight为0,直接使用remove()函数移除Map中键名为target的点,若target点存在,返回值为其原键值(int型),否则返回null。同理,根据Map类中put()方法的返回值,若输入权值weight不为0,直接使用put()函数修改Map中键名为target的点对应的键值为weight,若target点存在,返回值为其原键值(int型),否则返回null。定义Integer型变量pre记录两种分支下得到的返回值,若为null则返回0,否则返回对应int型变量。
重写Edge的equals函数与hashCode函数。定义标志变量name相同的两个点为同一个点,hashCode函数按照定义设计完成;
最后完成toString函数的重写。根据对称性,打印该点的终点集信息即可。这里为保证统一性保留3.3.3.1中“源点–权值->终点”的格式。
随后编写测试最上述方法逐一进行测试。
-
然后利用Vertex类实现ConcreteVerticesGraph类:
首先是成员与规约以及构造性的方法,同样的,构造性的方法只需给出一个空图。
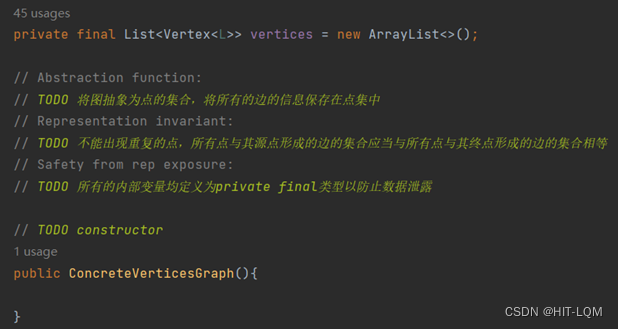
然后根据规约设计checkRep方法
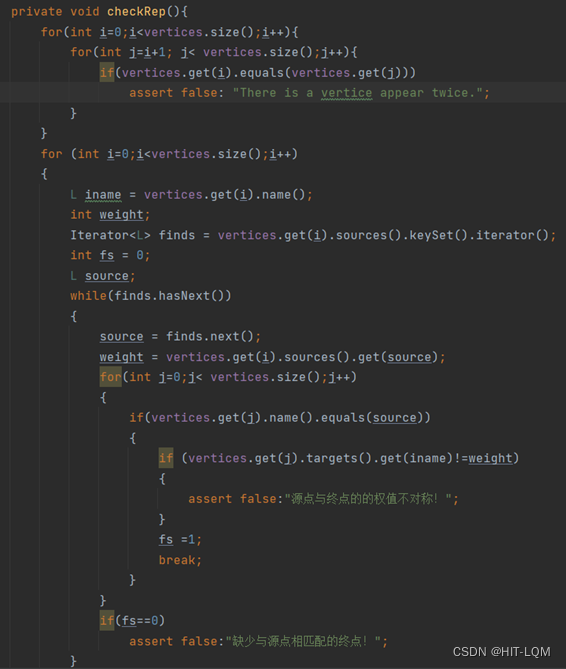
随后设计剩余的其他方法
public boolean add(L vertex):
根据函数规约,只需遍历vertices集合,查找有无与点vertex相同的点即可。若存在,则返回false;不存在,则在vertices集合中添加点vertex,然后返回true;
public int set(L source, L target, int weight):
根据函数规约,该方法主要分三种操作:修改已有的边,移除已有的边,添加新的边。因此,先遍历vertices集合,确定源点和终点是否存在。若源点存在,则在其终点集中进行setTargets操作;若终点存在,则在其源点集进行setSources操作。若某一端点不存在,则创建该点,设置对应的源点/终点集,然后在vertices集合加入新生成的点。返回值与对应setTargets/setSources操作返回值相同(checkRep()函数保证了setTargets/setSources操作返回值是相同的,返回任意一个即可)。
public boolean remove(L vertex):
根据函数规约,在vertices集合中找到vertex点,若找到,先将vertex从vertices集合中其他点的源点集与终点集中去除,然后在vertices集合中删除vertex并返回true;若未找到,直接返回false。
public Set<L> vertices()
根据函数规约,这里只需要返回由图的顶点构成的集合即可。构建一个新的集合,将vertices集合中所有点的标识加入该集合中即可。
public Map<L, Integer> sources(L target):
根据函数规约,直接返回target点的源点集即可。注意到保证数据信息不泄露,需要返回一个由target点的源点集复制的新集合。
public Map<L, Integer> targets(L source):
根据函数规约,直接返回source点的终点集即可。注意到保证数据信息不泄露,需要返回一个由source点的源点集复制的新集合。
public String toString():
函数需要将图的所有信息打印出来,即所有的点与边的信息。故先将所有的点的名称打印出来,随后遍历vertices集合,循环调用vertices类的toString方法即可
最后对上述的类设计测试,以此检验上述功能
调用IDEA的插件查看测试的覆盖度
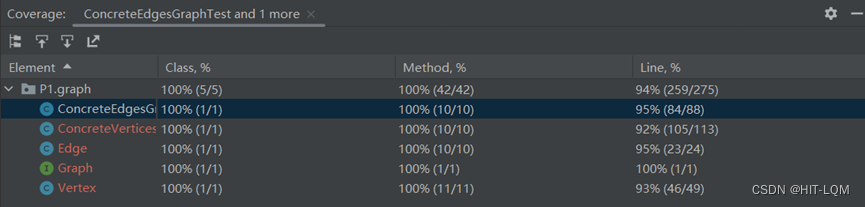
可以看到,我们的代码通过了上述的测试,并且测试的覆盖度接近100%,除了一小部分未达到,几乎覆盖了全部的空间,表明基本实现了预期的功能。
Problem 3: Implement generic Graph<L>
这一部分要求我们将原有的Graph<String>转化为泛型定义,注意同时要修改empty的方法。
Make the implementations generic
我们可以在声明中改为Graph<L>即可。
Implement Graph.empty()
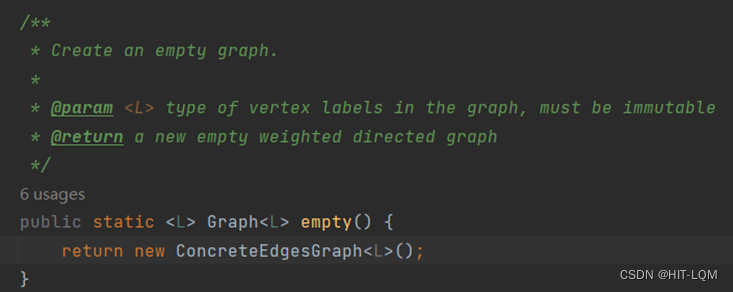
Problem 4: Poetic walks
这一部分要求我们借助刚刚实现的Graph类,来实现一个简单的语句扩充程序。
Test GraphPoet
对程序进行测试,分为以下三种情况:
- 空文件
- 单段文字
- 多段文字
我们后续将根据读入的处理好的文本来依次编写上述三个测试文本来满足测试空间。
Implement GraphPoet
此程序应该具备以下几个功能:
-
在读取.txt文件中的所有的单词,并将所有相邻的点添加到图中,这些边每出现一次会使得权值加1(初始权值设置为0)
-
读取后检查图是否合法
-
对目标字符串进行扩充:
首先要遍历给定文本的左右的单词,对于每一个单词,我们要找出该点所指向的终点集中权值最大的元素,将其添加在原来的两个单词之间。遍历结束后,返回扩充后的字符串。
-
全部实现后进行单元测试验证上述功能的正确性和健壮性。
经过设计和测试,代码测试结果如下:
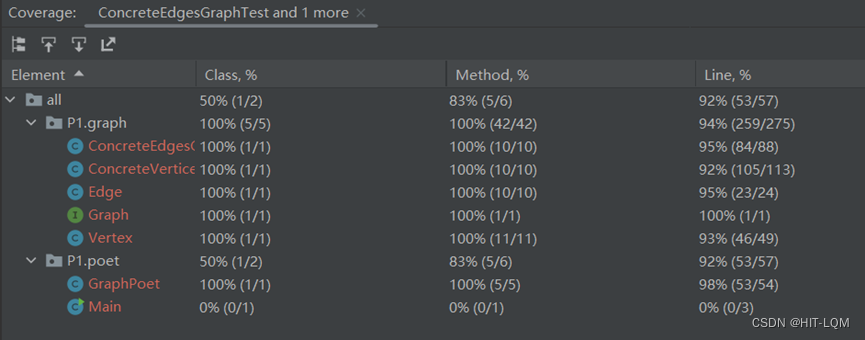
测试的覆盖度较高,测试均被通过,证明上述的程序基本符合了预期的要求。
Graph poetry slam
在这里按照要求添加一段代码,在main函数中添加一个测试样例“a cool example”
在这里改编了一段William Butler Yeats的短诗《Down By the Salley Garden》

随后测试一下:
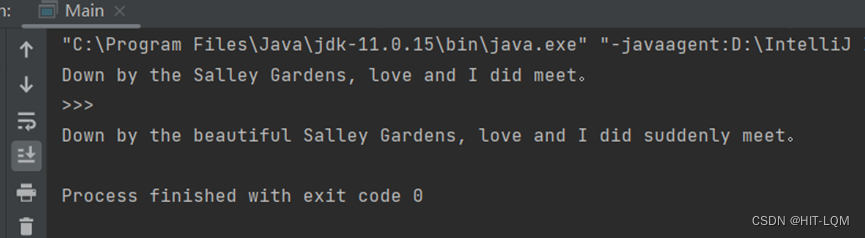
符合预期的结果。
Before you’re done
请按照http://web.mit.edu/6.031/www/sp17/psets/ps2/#before_youre_done的说明,检查你的程序。