https://download.csdn.net/download/yjw0911/19775978
下载链接
三维模型
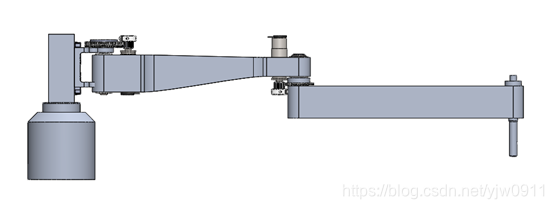
机器人运动学分析
机器人正运动学分析求解
采用D-H(Denavit-Hartenberg)方法建立的三自由度机器人基坐标系、各关节杆件坐标系和机器人末端坐标系如图 3 1所示。
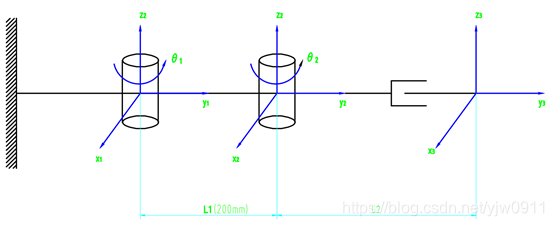
图 3 1三自由度机器人机构简图


机器人逆运动学分析求解
机器人逆运动学问题采用几何方法进行求解,由于机器人运动在平面内容运动,因此绘制平面内的机构简图,如下所示:

如图所示。其中,L1表示第一段臂长,固定长度为0.2m;L2表示第二段臂长,其为可变长度;r表示P点位置到原点位置的直线距离;θ1也表示第一段臂长与x轴的夹角,θ2也表示第二段臂长与第一段臂长延长线的夹角。
根据上述机构简图可知,将机器人简化成平面二连杆机构模型,机器人结构之间会互相影响,各个关节都存在一定的运动范围,第一段臂长运动范围为θ1【0°,180°】,第二段臂长运动范围θ3【-90°,90°】,平移关节的运动范围L2【0,0.2】。

轨迹规划与仿真
机器人模型建立
所设计的上肢康复机器人由多个连杆机构组成,其关节类型包括旋转关节和移动关节两种。利用Matlab中机器人仿真工具箱Robotics Tool中Link和SerialLink两个函数可建立上肢康复机器人模型[ ] 。其中,Link函数表达式如下:

式中,theta为关节变量;d为偏置距离;alpha为扭转角;a为连杆长度;sigma表示关节类型(0为旋转关节,1为移动关节);modified表示采用改进的D-H建模法,即前置坐标系法。前四个参数分别对应表1中的 , , , 。
具体程序编制如下:
Clear %情况matlab软件的数据缓存,避免影响本次运行
Clc %清空运行窗口的数据
L(1) = Link( ‘d’,0,‘a’,0,‘alpha’,0,‘qlim’,[-pi/2,pi/2], ‘modified’);
L(2) = Link( ‘d’,0,‘a’,2 ,‘alpha’,0 , ‘qlim’,[pi/2,pi], ‘modified’);
L(3) = Link( ‘theta’,0,‘a’, 0 , ‘alpha’, pi/2 , ‘qlim’,[0 , 2], ‘modified’);
RRP = SerialLink(L, ‘name’ , ‘RRP’); %建立三自由度模型RRP.display(); %显示建立的机器人的DH参数
RRP.plotopt = {‘workspace’,[-10,10,-10,10,-10,10],‘tilesize’,10}; %设置模型空间大小和地砖大小
RRP.teach; %画出模型并进行调控
RRP.plot([0 pi/2 2]) %输入一定参数后机器人图形
运行上述程序,即可得到三自由度机器人模型如图 3-3(为了显示明显,L1连杆长度放大25倍)
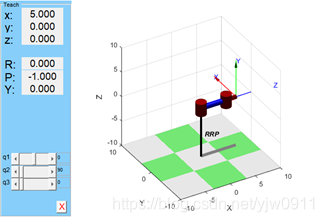
图 3 3三自由度机器人模型
机器人运动空间计算
依据机器人三个自由度的运动范围,采用三自由度机器人模型进行计算。采用蒙特卡洛方法,通过Matlab编程,程序如下:
N=30000; %随机样本的总数
%关节角度限制
limitmax_1 = 90; %关节1最大角度
limitmin_1 = -90; %关节1最小角度
limitmax_2 = 180; %关节2最大角度
limitmin_2 = 90; %关节2最小角度
limitmax_3 = 2;%关节3最大距离
limitmin_3 = 0; %关节3最小距离
%得到三自由度
theta1=(limitmin_1+(limitmax_1-limitmin_1)*rand(N,1))*pi/180; %关节1限制
theta2=(limitmin_2+(limitmax_2-limitmin_2)*rand(N,1))*pi/180; %关节2限制
theta3=(limitmin_3+(limitmax_3-limitmin_3)*rand(N,1)); %关节3限制
qq=[theta1,theta2,theta3];%随机样本的三个自由度的矩阵
Mricx=RRP.fkine(qq);%机器人逆运动学求解
x=reshape(Mricx(1,4,:),N,1);%分解得到x方向的位置
y=reshape(Mricx(2,4,:),N,1); %分解得到y方向的位置
z=reshape(Mricx(3,4,:),N,1); %分解得到z方向的位置
plot3(x,y,z,‘b.’,‘MarkerSize’,0.5);%画出所有落点位置
hold on;
绘制得到的机器人运动空间如图 3 4所示,图中运动空间呈扇形。
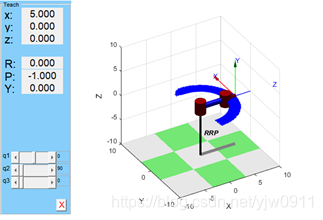
图 3 4机器人XOY平面运动空间
机器人运动轨迹规划
本文所设计的三自由度机器人是一种RRP机构,即两个旋转自由度+一个平移自由度组成。机器人想要按指定的轨迹进行运动,就需要进行轨迹规划,提前将机器人每个自由度的运动情况设定好,这也是本文研究的重点内容。
已知,轨迹规划可以在关节空间或者笛卡尔坐标空间进行[ ]。在关节空间进行轨迹规划,虽然方法简单,不会产生奇异点,但是,却不能使机器人末端产生精确的轨迹;而在笛卡尔坐标空间进行轨迹规划,虽然可以规划机器人末端位姿,准确实现运动路径。
笛卡尔坐标轨迹规划的方法有很多种,现在采用两种方法进行对比分析:五次多项式轨迹规划和匀加速匀减速方法。
已知P1起点和P2终点,并设置40步进行规划
init_ang=[0 pi/2 0];%p1起点
targ_ang=[pi/4,pi/2,2];%p2终点
step=40;%轨迹分为40步
五次多项式轨迹规划
%jtraj,已知初始和终止的关节角度,利用五次多项式来规划轨迹。
[q,qd,qdd] = jtraj(init_ang, targ_ang, step);
RRP.plot(q); %绘制机器人模型
hold on
通过matlab运行上述程序,得到下列运动轨迹、位置曲线图、速度曲线图和加速度曲线图,如下图所示:

机器人实际运动轨迹
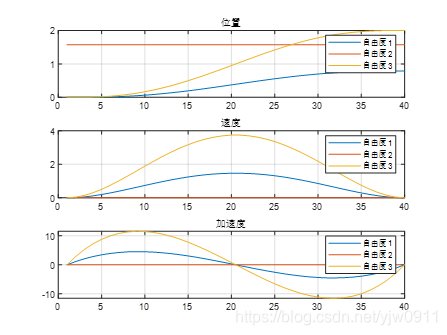
机器人每个自由度运动曲线图
从上图可知,五次多项式轨迹规划的位置曲线图、速度曲线图和加速度曲线图的曲线都很平滑,机器人在运动过程中也会很平稳,不会出现很大的冲击,对机械结构的要求也很低,因此此方方法较好。
匀加速匀减速轨迹规划
%figure(3)
p1 = RRP.fkine(init_ang);%运动学正解
p2 = RRP.fkine(targ_ang);%运动学正解
Tc=ctraj(p1,p2,step);%运用的是匀加速匀减方法
Tjtraj=transl(Tc);
plot2(Tjtraj,‘r’);
title(‘p1到p2直线轨迹’);
grid on;
通过matlab运行上述程序,得到下列运动轨迹、位置曲线图、速度曲线图和加速度曲线图,如下图所示:
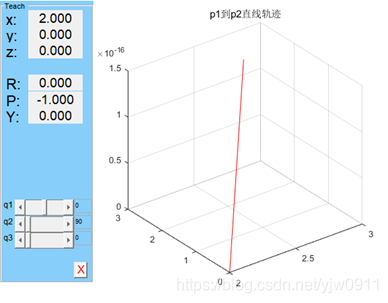
机器人实际运动轨迹
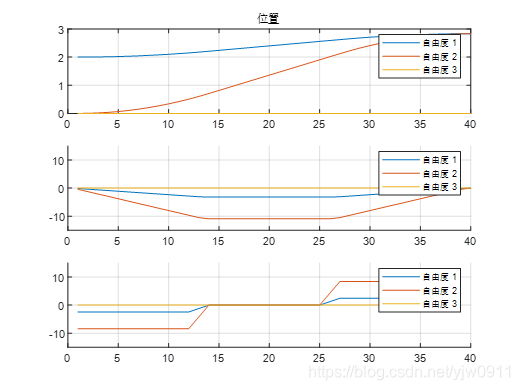
机器人每个自由度运动曲线图
从上图可知,匀加速匀减速轨迹规划的位置曲线图、速度曲线图都很平滑,但是和加速度曲线图曲线有突变情况,也符合匀加速匀减速的规律,说明轨迹方法的正确行。
结论:对匀加速匀减速轨迹规划与五次多项式轨迹规划的方法,可知该三自由度机器人轨迹规划更适合材料五次多项式轨迹规划的方法。